残差是啥意思？

Posted 2023-05-18

残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话， 我们可以将残差看作误差的观测值。
它应符合模型的假设条件，且具有误差的一些性质。利用残差所提供的信息，来考察模型假设的合理性及数据的可靠性称为残差分析。
有多少对数据，就有多少个残差。残差分析就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰。

拓展资料：

普通残差

设线性回归模型为

 

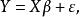
其中Y是由响应变量构成的n维向量，X是

 

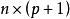
阶设计矩阵，β是p+1维向量，ε是n维随机变量。

回归系数的估计值

 

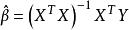
，拟合值

 

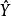
为

 

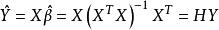
，其中

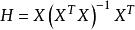
，称H为帽子矩阵。残差为

 

。

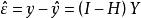
这解释了帽子矩阵与残差的关系，因为残差可以通过帽子矩阵与真实值得出。

在回归分析中，测定值与按回归方程预测的值之差，以δ表示。残差δ遵从正态分布N(0，σ2)。（δ-残差的均值）/残差的标准差，称为标准化残差，以δ*表示。δ*遵从标准正态分布N(0，1)。实验点的标准化残差落在(-2，2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2，2)区间以外，可在95%置信度将其判为异常实验点，不参与回归直线拟合。

显然，有多少对数据，就有多少个残差。残差分析就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰。

残差分析（residual analysis）就是通过残差所提供的信息，分析出数据的可靠性、周期性或其它干扰 。用于分析模型的假定正确与否的方法。所谓残差是指观测值与预测值（拟合值）之间的差，即是实际观察值与回归估计值的差。在回归分析中，测定值与按回归方程预测的值之差，以δ表示。残差δ遵从正态分布N(0，σ2)。

（δ-残差的均值）/残差的标准差，称为标准化残差，以δ*表示。δ*遵从标准正态分布N(0，1)。实验点的标准化残差落在(-2，2)区间以外的概率≤0.05。若某一实验点的标准化残差落在(-2，2)区间以外，可在95%置信度将其判为异常实验点，不参与回归线拟合。显然，有多少对数据，就有多少个残差。

参考技术A 残差（residuals）。

大体上说，残差就是结果的误差。
举个栗子：

有一个函数 f(x) = b.

我们想求得其中的 x的值。 现在有一个x的近似值x0，那么:

残差(residuals) = f(x0) - b.

误差（error) = x - x0

当然很多情况下，我们只有x的近似值x0，所以残差是可以求得的，但是误差不能。

回归分析中的均方怎么算?回归和残差的均方（MS）怎么算？

回归分析中的均方怎么算?回归和残差的均方（MS）怎么算？

回归平方和＝自由度×均方

残差均方＝残差平方和×残差df

残差F＝回归均方÷残差均方

回归是方法，残差在数理统计中是指实际观察值与估计值(拟合值)之间的差，平方和有很多个，不同的平方和的意思不一样，与样本量及模型中自变量的个数有关，样本量越大，相应变异就越大。

df是自由度，是自由取值的变量个数；

均方指的是一组数的平方和的平均值，在统计学中，表示离差平方和与自由度之比；

f是f分布的统计量，用于检验该回归方程是否有意义；

SIG=significance，意为“显著性”，后面的值就是统计出的P值，如果P值0.01<P<0.05,则为差异显著，如果P<0.01,则差异极显著。

扩展资料：

线性回归使用最佳的拟合直线（也就是回归线）在因变量（Y）和一个或多个自变量（X）之间建立一种关系。

多元线性回归可表示为Y=a+b1*X +b2*X2+ e，其中a表示截距，b表示直线的斜率，e是误差项。多元线性回归可以根据给定的预测变量（s）来预测目标变量的值。

逻辑回归是用来计算“事件=Success”和“事件=Failure”的概率。当因变量的类型属于二元（1 / 0，真/假，是/否）变量时，应该使用逻辑回归。这里，Y的值为0或1，它可以用下方程表示。

参考资料来源：百度百科-回归分析

参考技术A 回归平方和＝自由度×均方
残差均方＝残差平方和×残差df
残差F＝回归均方÷残差均方