小样本大概率事件的正确处理方式 - 3. 实际使用

Posted 2023-02-20 EZhex1991

在之前的两篇文章中，我主要对概率约束和样本约束做了比较。
（详情点击 《小样本大概率事件的正确处理方式 - 1. 概率的含义和误差产生的原因》 和 《小样本大概率事件的正确处理方式 - 2. 结果分析》）
结论简单点说就是：概率约束误差大，但是简单；样本约束精确，但是复杂。

从其复杂度上去比较，产生n次随机事件，概率约束的时间复杂度是O(n)，空间复杂度是O(1)。而样本约束，由于要提前将样本进行洗牌，其时间复杂度是O(n^2)，而为了存放洗牌结果，其空间复杂度是O(n)（实际上应该是和约束样本的大小相关）。

然而前两篇文章只是为了表现两种约束的含义，而并不是我们在写代码时要使用的算法。为了将其区别更清晰地展现出来，我在样本约束中提前处理好了样本，但这并不是必要的。

样本约束的实际目的，是让每个约束周期中（总体样本的数量是我们的约束样本数量的整数倍时就是一个周期）各事件的出现频次与预期完全相符。所以，我们并不需要在第一次随机时就知道最后一次随机的结果，我们只需要知道某一次随机时，各种事件还能在本次约束周期中出现多少次——每次随机后，下一次随机条件会出现相应变化，这就是“动态”的含义。

和上一篇文章的例子一样：我们有一个10大小的约束样本，该样本中0,1,2分别出现2,3,5次。
我们并不需要在第一次随机时对样本进行洗牌，只需要在第n次随机后，记录0,1,2分别出现过的次数（或剩余可出现的次数），然后获取一个[0,剩余事件-1]的随机数即可。比如第6次随机后统计0出现了1次，1出现了2次，2出现了3次，那么周期剩余的4次中，0,1,2分别可以出现1,1,2次，第7次随机我只需要取一个[0,3]的随机数即可。

对实例进行范化描述（公式化）就是：样本大小为S，事件a的出现概率为P(a)，在第n-1次随机后a出现了T(a)次，那么第n次随机中a出现的概率就是(S * P(a) - T(a)) / (S - n)。这就是我标题中的动态概率约束——它的实质就是样本约束（限制事件频次），但是其计算方式却与概率约束一样（看随机数落在那个区间）。这个结果会与上一篇文章提到的样本约束完全一样。

从另一个角度再次考虑一下这个问题：既然每个约束周期里面的事件发生频次都已经订好了，那无论该约束样本里的事件是如何排列的，概率都会在周期结束时得到保证。如果我对概率波动并不关心，我只需要限制样本次数，是不是就只需要关注剩余事件种类，而不需要关注剩余事件的出现概率呢？

仍然是之前的例子：约束样本大小为10，0,1,2分别出现2,3,5次。每次随机时都取[0,2]的随机整数，这个数直接作为事件。如第6次随机0,1,2分别出现了1,2,3次，那么第7次卧仍然从[0,2]中选取，如果第7次选中了0，那么0就不可能再出现了，剩余事件就只有1,2两种了，那么第8次的随机则取[0,1]。

范化描述为：样本大小为S，a是其中一种并且其期望概率为P(a)，在第n-1次随机时有C种可能的互斥事件，并且a出现了S*P(a)-1次，那么第n-1次所有的事件概率都是1/C，如果第n-1次随机结果为a，那么a的概率就变为0，其他互斥事件的概率变为1/(C-1)。这就是标题中的动态事件约束——它的实质也是样本约束，但是其计算方式只和当前随机事件的种类有关，换句话说，所有当前可能出现的事件概率都相同，如果某个事件发生的次数达到了期望值，那么这个事件就不再是“可能出现的事件”。

---

这次的曲线分析我稍微做一下调整，将约束样本的大小定为200，总样本还是1000，也就是说，对于样本约束（包括本篇所说的动态概率约束和动态事件约束），总样本有5个约束周期。四种约束的样本生成代码和曲线图如下：

概率约束：

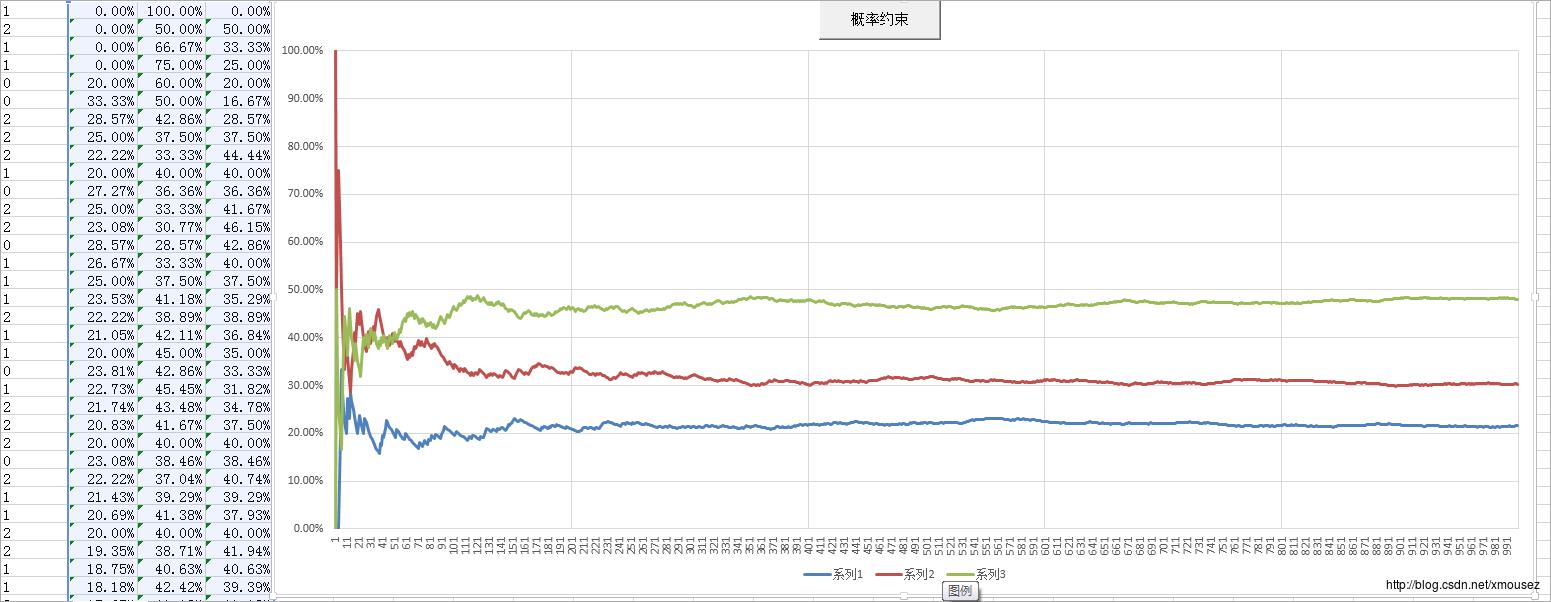
样本约束：

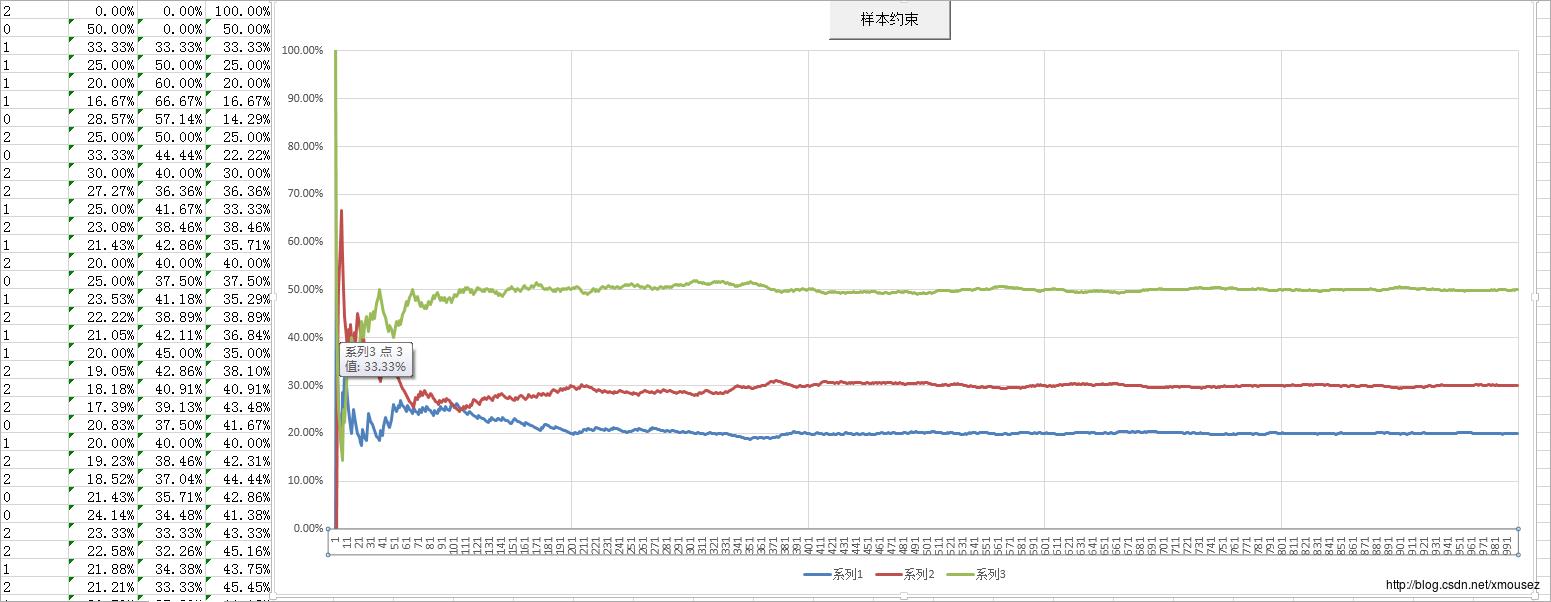
动态概率约束：

动态事件约束：

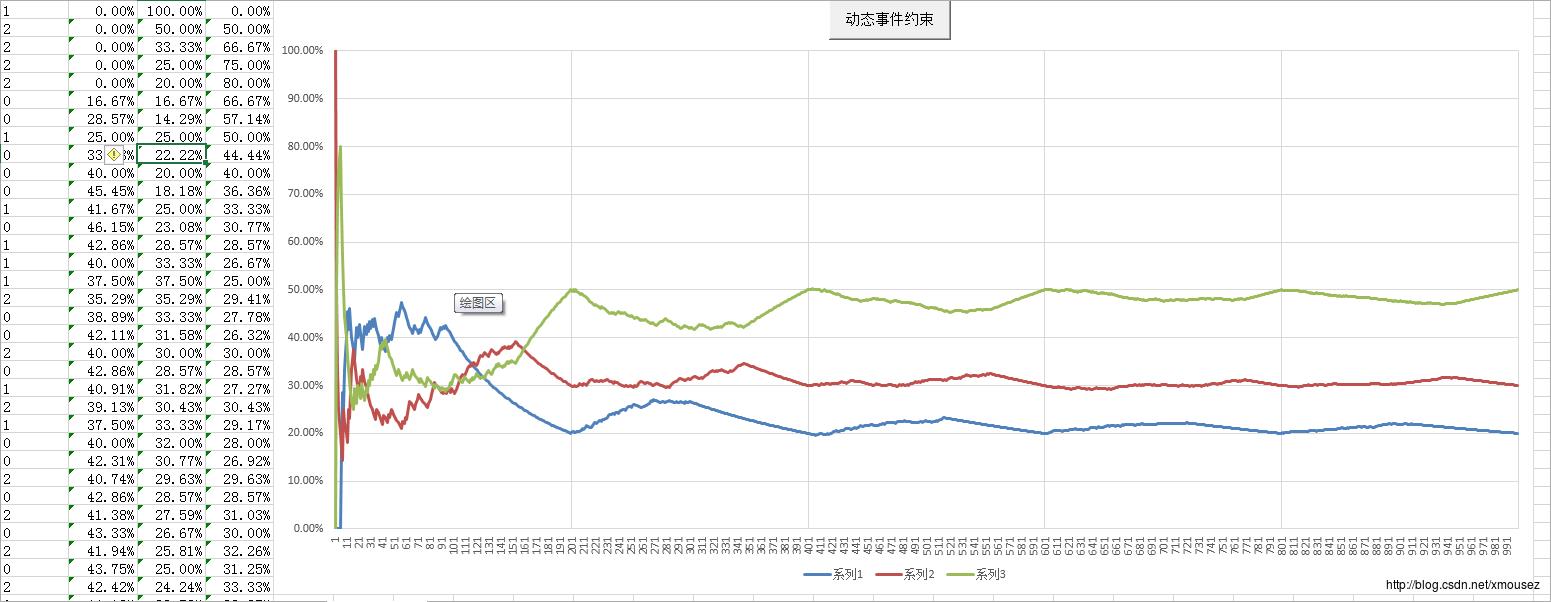
对比就可以看出，动态概率约束作为样本约束的优化，在一个周期后二者的稳定性没有差别；而对于动态事件约束，曲线会呈现周期性波动，波动周期则与约束周期相同，在每个波动周期中，各事件概率先趋向均值，然后再趋向实际概率。

对于动态概率约束，实际上就是样本约束的优化，所以所有的随机事件，都可以——并且理论上应该——用动态概率约束（当动态概率约束的约束样本大小为无限大时，其等价于普通概率约束）；
而对于动态事件约束，则是在动态概率约束上偷了一下懒，将当前所有可能事件视为等概率，免去了依次判断某个事件是否发生的过程（取的随机整数就能做事件），事件的可能性越多，能够节省的开销就越大。

最后给出一个动态事件约束的使用情景：如果概率和样本是以游戏世界来说的（用户无感知），并且概率只是为了保证稀有物品的“稀有度”，那么你就不用在乎这个物品爆率的周期波动（事实上这种周期性波动反倒有可能有益于用户留存）。

我一直在洗澡，油腻的师姐在哪里？屠龙宝刀，点击就送，极品装备，一秒刷爆？醒醒吧，游戏为了赚钱啥事都干得出来~