高斯混合模型

Posted 2023-05-15

参考技术A 多元高斯分布概率密度函数:       1.1

其中 是 维均值向量， 是 协方差矩阵。

定义高斯混合分布:

    1.2

为混合系数，满足

假设数据集 是由高斯混合模型生成的, 令随机变量 表示生成样本的高斯混合成分(即类标签)，对于聚类问题，我们需要求出

E步:

对于某个样本 ，根据贝叶斯公式，它由第 个高斯混合成分生成(或属于 类)的后验概率概率:

    1.3

由于先验概率  ，而条件概率密度 恰好是对应高斯成分的密度函数，因此3.3可写为：

    1.4

给出了样本 由第 个高斯成分生成的后验概率, 记为 ，为隐变量。

M步:

给定样本集 , 数据集中样本对分布的对数似然函数为:

   

      1.5

对似然函数中的变量求偏导

    1.6

令 ，得:

 两端同时左乘 ，并将 代入，得:

      1.7

解出     1.8

的求法参考 矩阵求导术 ，个人认为是比较好的矩阵求导方法。

首先记

根据矩阵求导术，先求 的全微分，把 当做变量，其余看做常数

其中

每个样本独立同分布，所以协方差矩阵 (该矩阵为实对称矩阵)正定，因此可逆

由 、 和 得:

化简得:

标量套上迹 并在迹内交换次序得，

对照全微分与导数的关系 有:

因此，     1.9

令1.9 为0 , 将方程左右同时乘以 ,并将 代入得:

    1.10

解得：     1.11

高斯混合成分的系数 可由Lagrange乘数法求出，注意到 , 

设     1.12

    1.13

    1.14

代入1.13得:

     1.15

以上步骤不断迭代直至算法收敛。

        在半监督学习中，一部分数据是有类标签的，记为 ，另一部分是没有标签的，记为 。

对于有监督信息的数据 ，我们仍假设每个样本 又混合高斯分布生成。给定样本 ，其真实样本标记为 ，其中

为所有可能的类别。

因此     2.1

其中混合系数 。

        令 表示模型 对 的预测标记， 表示样本 隶属的高斯混合成分。模型需要最大化后验概率，即：

    2.2

其中

    2.3

由于第 类样本只能由同样标号的高斯混合成分生成的，所以必有 ,否则 。

对 求似然， 注意 项与高斯混合聚类的似然函数相同:

    2.4

其中分母部分是数据的概率密度, 对似然无影响，可以去掉，因此 等价于

    2.5

E步：根据当前模型参数计算未标记样本 属于各高斯混合成分的概率(同高斯混合聚类)

    2.6

M步：基于 更新模型参数，这里跟高斯混合聚类的区别就是似然函数不同。

分别计算 。 部分的值在第一部分中已经计算过，现只需要计算 部分的值。

由于带监督信息， 内部只剩第 项，其余均为 。

所以

    2.7

故     2.8

令其为 ，求得：

    2.9

其中 是 中属于第 类的样本标记数目

协方差同理，只计算 部分，

    2.10

故

    2.11

令其为 ，求得：

    2.12

同理用Lagrang乘数法求得：

    2.13

以上过程迭代直至算法收敛。

Reference:

《机器学习》 周志华

《统计学习方法》 李航

知乎专栏：矩阵求导术(上)

语音识别基于高斯混合模型（GMM）的语音识别matlab源码

一、简介

1 高斯混合模型概述

高斯密度函数估计是一种参数化模型。高斯混合模型（Gaussian Mixture Model, GMM）是单一高斯概率密度函数的延伸，GMM能够平滑地近似任意形状的密度分布。高斯混合模型种类有单高斯模型（Single Gaussian Model, SGM）和高斯混合模型（Gaussian Mixture Model, GMM）两类。类似于聚类，根据高斯概率密度函数（Probability Density Function, PDF）参数不同，每一个高斯模型可以看作一种类别，输入一个样本x，即可通过PDF计算其值，然后通过一个阈值来判断该样本是否属于高斯模型。很明显，SGM适合于仅有两类别问题的划分，而GMM由于具有多个模型，划分更为精细，适用于多类别的划分，可以应用于复杂对象建模。
1.1 单高斯模型

1.2 高斯混合模型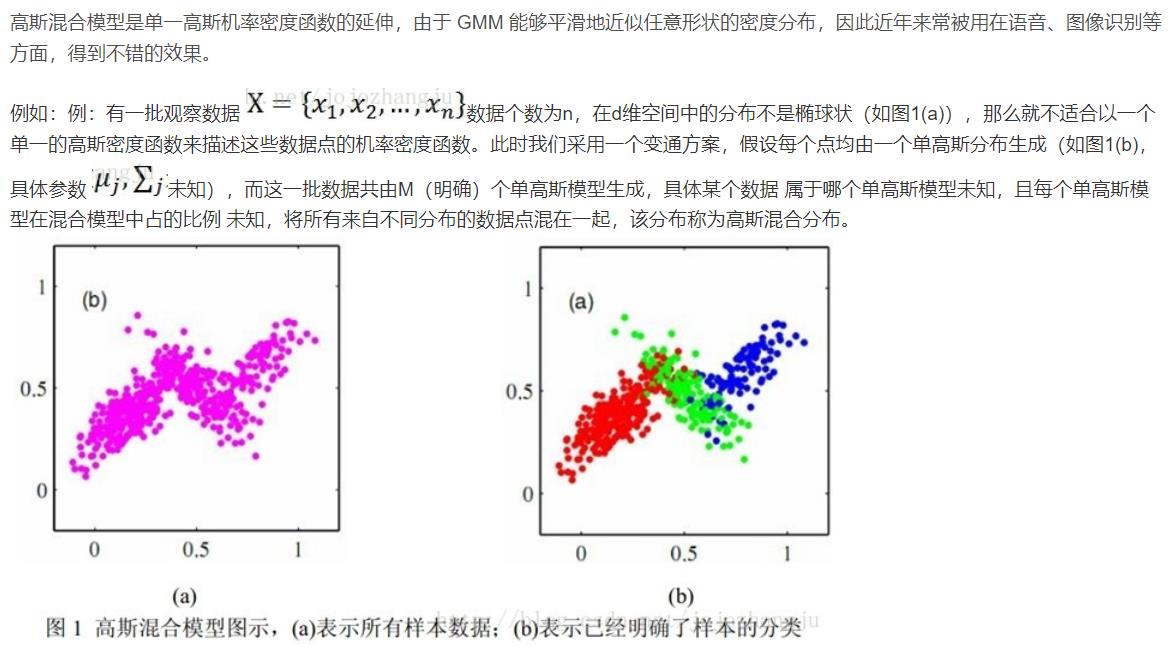



2 高斯混合模型参数估计

2.1 样本分类已知情况下的GMM

二、源代码

function mix=gmm_init(ncentres,data,kiter,covar_type)
%% 输入：
% ncentres:混合模型数目
% train_data:训练数据
% kiter:kmeans的迭代次数
%% 输出：
% mix:gmm的初始参数集合
 
 
[dim,data_sz]=size(data');
 
mix.priors=ones(1,ncentres)./ncentres;
mix.centres=randn(ncentres,dim);
switch covar_type
case 'diag'
  % Store diagonals of covariance matrices as rows in a matrix
  mix.covars=ones(ncentres,dim);
case 'full'
  % Store covariance matrices in a row vector of matrices
  mix.covars=repmat(eye(dim),[1 1 ncentres]);
otherwise
  error(['Unknown covariance type ', mix.covar_type]);  
end
 
 
% Arbitrary width used if variance collapses to zero: make it 'large' so
% that centre is responsible for a reasonable number of points.
GMM_WIDTH=1.0;
 
%kmeans算法
% [mix.centres,options,post]=k_means(mix.centres,data);
[mix.centres,post]=k_means(mix.centres,data,kiter);
 
% Set priors depending on number of points in each cluster
cluster_sizes = max(sum(post,1),1);  % Make sure that no prior is zero
mix.priors = cluster_sizes/sum(cluster_sizes); % Normalise priors
 
switch covar_type
case 'diag'
  for j=1:ncentres
   % Pick out data points belonging to this centre
   c=data(find(post(:,j)),:);
   diffs=c-(ones(size(c,1),1)*mix.centres(j,:));
   mix.covars(j,:)=sum((diffs.*diffs),1)/size(c,1);
   % Replace small entries by GMM_WIDTH value
   mix.covars(j,:)=mix.covars(j,:)+GMM_WIDTH.*(mix.covars(j,:)<eps);
  end 
case 'full'
  for j=1:ncentres
   % Pick out data points belonging to this centre
   c=data(find(post(:,j)),:);
   diffs=c-(ones(size(c,1),1)*mix.centres(j,:));
   mix.covars(:,:,j)=(diffs'*diffs)/(size(c,1)+eps);
   % Add GMM_WIDTH*Identity to rank-deficient covariance matrices
   if rank(mix.covars(:,:,j))<dim
	mix.covars(:,:,j)=mix.covars(:,:,j)+GMM_WIDTH.*eye(dim);
   end
  end
otherwise
  error(['Unknown covariance type ', mix.covar_type]);
end
 
mix.ncentres=ncentres;
mix.covar_type=covar_type;
 
%=============================================================
function [centres,post]=k_means(centres,data,kiter)
 
[dim,data_sz]=size(data');
ncentres=size(centres,1); %簇的数目
[ignore,perm]=sort(rand(1,data_sz)); %产生任意顺序的随机数
perm = perm(1:ncentres); %取前ncentres个作为初始簇中心的序号
centres=data(perm,:); %指定初始中心点
id=eye(ncentres); %Matrix to make unit vectors easy to construct
for n=1:kiter
  % Save old centres to check for termination
  old_centres=centres; %存储旧的中心,便于计算终止条件
  
  % Calculate posteriors based on existing centres
  d2=(ones(ncentres,1)*sum((data.^2)',1))'+...
     ones(data_sz,1)* sum((centres.^2)',1)-2.*(data*(centres')); %计算距离
 
  % Assign each point to nearest centre
  [minvals, index]=min(d2', [], 1);
  post=id(index,:);
 
  num_points = sum(post, 1);
  % Adjust the centres based on new posteriors
  for j = 1:ncentres
    if (num_points(j) > 0)
      centres(j,:) = sum(data(find(post(:,j)),:), 1)/num_points(j);
    end
  end
 

三、运行结果

四、备注

完整代码或者代写添加QQ1575304183