请问用indesign排书 要留出血吗？留四边出血吗？

Posted 2023-05-12

200多页的书
我没排过书 一直都是排杂志 所以想问问~

要留的，由于工作关系，我也没有接触过出版。我的一个朋友说留出血是为了防止边距过小时在裁切的过程中裁切到文字，一般留下3mm。也就是说不一定用，但是习惯上留的。 参考技术A 新建文件默认有3mm出血，均在页面外（对版的话书脊边没有）。
你按成品尺寸做文件，需出血的内容让它超出页面3mm或者以上。
输出PDF时，在参数设定中设置：标记和出血--使用文件出血设定。本回答被提问者采纳 参考技术B 知道为什么要做出血吗！因为印厂在印刷好东西后还要裁切！由于有误差不可能那么准要是不做出血，裁切时又出现点误差那成品尺寸里就不漏白边了啊！追问

我知道啊 所以我问是不是留四边

参考技术C 书脊那边不用出血

[dfs] aw180. 排书(IDA*+dfs深入理解+思维+好题)

文章目录

• • 1. 题目来源
  • 2. 题目解析

1. 题目来源

链接：180. 排书

相关链接：

• [A*] aw179. 八数码(A*+bfs最小步数模型+模板题)
  
• [A*] aw178. 第K短路(A*+bfs最小步数模型+好题)
  
• [dfs] aw170. 加成序列(dfs迭代加深+模板题)

2. 题目解析

IDA* 就是 基于迭代加深的 A * 算法。

在 迭代加深 dfs 的基础上加上 A* 算法的剪枝就很就是 IDA*。即，在 dfs 过程中，针对每个节点都用估价函数估计它距离答案至少需要 dfs 多少层，如果当前层数加上估价层数大于了迭代加深设定的层数的话，很明显当前分支及以后的分支都是无法找到答案的，所以就可以直接剪枝了。

要求针对节点的估价距离一定要小于等于真实距离。

手写笔记，乱！

---

针对本题。

首先的首先，确定搜索顺序：枚举所有可选长度的连续区间，再枚举这些区间能放到的所有位置，就能枚举到所有方案。

估价函数设计：

• 定义序列中每个数的后缀不匹配的情况。
• 后缀匹配指的是当前序列位置上的数的后一个数刚好比当前位置的数大 1。
• 终点序列是 123456… ，它们的后缀都是匹配的。
• 针对当前节点状态，统计不匹配的后缀数量。一次的状态更新最好可以修复三个后缀数量，假设当前状态有 t 个后缀不匹配的位置，那么每次最多修复 3 个，至少需要修复 $\lceil \frac{t}{3}\rceil$ 次。即 dfs 至少需要再向下递归 $\lceil \frac{t}{3}\rceil$ 层才有可能搜到正确答案。
• 可以以此配合迭代加深 depth 设置，来进行剪枝。

---

每个状态都是一组数，用数组存储。每次的状态更新、恢复现场都可以借鉴八数码问题的 backup 备份设计。

在此，同理可开一个 backup[N] 数组作为 局部变量 来存每个状态的当前层情况，dfs 向下递归时就直接在当前状态的数组中进行状态更新。状态需要回溯时，就用 backup 中备份的状态进行回溯即可。

但是显然这样做，每个节点都需要开一个局部变量数组来进行状态备份…空间复杂度就是 $O(n)$ 的了。

我们需要理解：

• 在 dfs 过程中栈内不会出现同层的节点。一条 dfs 路径一定是随着深度递增的。
• 在回溯时，只需要当前路径中上面各层节点的状态，跟已经遍历过的节点、没遍历的节点、根本扯不上关系的节点都无关。
• 所以，我们只需要开一个全局数组，w[5][N] 用来存 dfs 每一层节点的状态，针对每条路径，只会存每层的一个节点的状态。
• w[5][N] 数组中的状态就是反复覆盖使用，但能保证正确的回溯时的恢复现场。
• 这样就将空间复杂度从 $O(n)$ 优化到 $O(logn)$ 了。 是一个非常棒的优化！
• 但实际上，这两者在时间复杂度上是一样的。

具体看手写笔记吧，写的很详细：

---

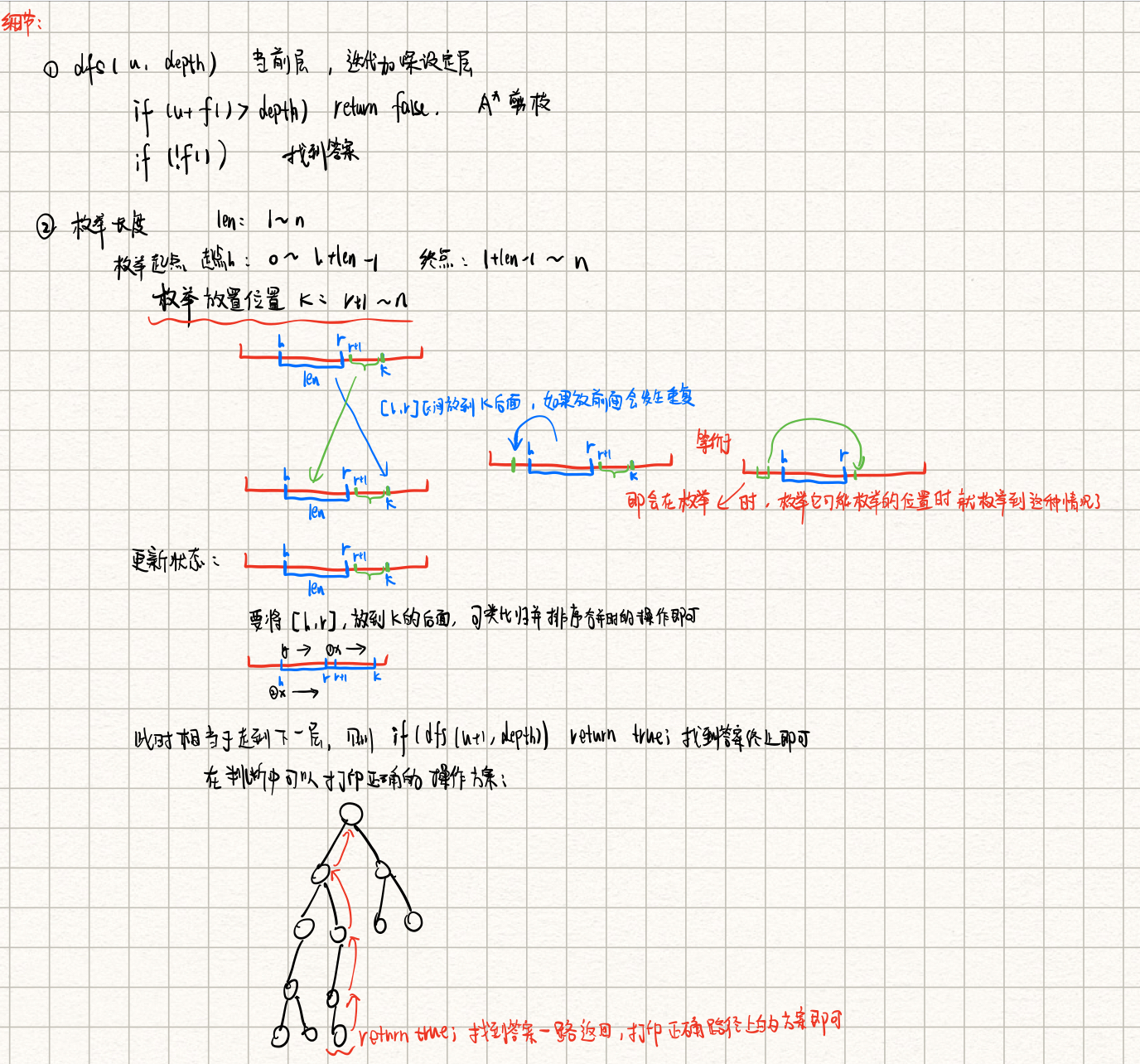
时间复杂度：$O(560^4)$，实际上使用 IDA* 后状态很少

空间复杂度：$O(5n)$

---

全局变量：

#include <iostream>
#include <cstdio>
#include <cstring> 
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int p[N];           // 临时存当前层的状态
int w[5][N];        // 备份，记录当前状态，用于回溯时的状态恢复，直接拷贝恢复为之前原状态即可

// 统计后缀不匹配的个数，返回距离有序的最小操作步数，有序时返回 0
int f() {
    int res = 0;
    for (int i = 1; i < n; i ++ )
        if (p[i] != p[i - 1] + 1)
            res ++ ;
    
    return (res + 2) / 3;                   // 上取整，得到当前状态距离最终状态的最小距离
}

bool dfs(int u, int depth) {
    if (u + f() > depth) return false;      // 启发式剪枝
    if (!f()) return true;                  // 当估价函数返回 0，等价于排好序了

    for (int len = 1; len <= n; len ++ )                // 枚举区间长度
        for (int l = 0; l + len - 1 < n; l ++ ) {       // 枚举区间起点、终点
            int r = l + len - 1;
            for (int k = r + 1; k < n; k ++ ) {         // 枚举区间防止位置，放到 k 的后面
                memcpy(w[u], p, sizeof p);              // 备份当前状态
                
                // 状态更新，需要将 len 这段放到 k 的后面
                // [r+1, k] 需要放到 [l, r] 的前面，类比归并排序
                int y = l;
                for (int x = r + 1; x <= k; x ++ , y ++ ) p[y] = w[u][x];
                for (int x = l; x <= r; x ++ , y ++ ) p[y] = w[u][x];

                if (dfs(u + 1, depth)) return true;
                
                /*
                 * 打印当前层的正确状态，可以看到是怎么进行 5 步内更改的 
                 * 递归，是按状态倒序打印的，且最终有序时，会在 if (!f()) return true; 直接 return ; 
                 * 不会打印有序的状态
                if (dfs(u + 1, depth)) {
                    for (int i = 0; i < n; i ++ ) cout << w[u][i] << ' ';
                        cout << endl;
                    return true;
                }
                */

                memcpy(p, w[u], sizeof p);          // 恢复现场
            }
        }

    return false;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T -- ) {
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ ) scanf("%d", &p[i]);   // 初始状态

        int depth = 0;
        while (depth < 5 && !dfs(0, depth)) depth ++ ;      // 层数小于 5 且没搜到答案，则迭代加深继续搜

        if (depth >= 5) puts("5 or more");
        else printf("%d\\n", depth);         
    }

    return 0; 
}

---

局部变量：

#include <iostream>
#include <cstdio>
#include <cstring> 
#include <algorithm>

using namespace std;

const int N = 15;

int n;
int p[N];           // 临时存当前层的状态

int f() {
    int res = 0;
    for (int i = 1; i < n; i ++ )
        if (p[i] != p[i - 1] + 1)
            res ++ ;
    
    return (res + 2) / 3;                 
}

bool dfs(int u, int depth) {
    if (u + f() > depth) return false;    
    if (!f()) return true;                 

    int w[N];		// 针对每个节点，都开一个空间，用来存储原状态，用于回溯
    for (int len = 1; len <= n; len ++ )                
        for (int l = 0; l + len - 1 < n; l ++ ) {       
            int r = l + len - 1;
            for (int k = r + 1; k < n; k ++ ) {        
                memcpy(w, p, sizeof p);             
                int y = l;
                for (int x = r + 1; x <= k; x ++ , y ++ ) p[y] = w[x];
                for (int x = l; x <= r; x ++ , y ++ ) p[y] = w[x];
                if (dfs(u + 1, depth)) return true;
                memcpy(p, w, sizeof p);      
            }
        }

    return false;
}

int main() {
    int T;
    scanf("%d", &T);

    while (T -- ) {
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ ) scanf("%d", &p[i]);   

        int depth = 0;
        while (depth < 5 && !dfs(0, depth)) depth ++ ;     

        if (depth >= 5) puts("5 or more");
        else printf("%d\\n", depth);         
    }

    return 0; 
}