矩阵的特征值求解
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵的特征值求解相关的知识,希望对你有一定的参考价值。
baidu展开追问
追问
1
2
2(2
1
-2)
刚才题目弄错了,最后a33=1,麻烦了,这样的话是不是3,3,-3
2
-2
1
回答
改过来特征值3,3,-5
追问
我是这样求的,解出来是-3,
3
,3?
回答
是的,不好意思,是-3,3,3。特征值的和等于对角线各元素之和
追问
那我想知道的是,在这个矩阵下的二次型,如果用lambdaE-A求和用矩阵的初等变换求,特征值是有区别的吗?初等变换后PtAP成了一个对角阵,这三个数一定是这个矩阵的特征值一样么?我求的怎么不一样,不是-3,3,3
回答
相似矩阵P﹣¹
A
P的特征值相同,合同矩阵PT
AP只能说明正负惯性指数相等,此题中PT
AP化成的对角阵只能说明它有两个正的特征值,一个负的特征值。
寒烟hy123
2014-01-15
1
0
分享 参考技术A ax=mx,等价于求m,使得(me-a)x=0,其中e是单位矩阵,0为零矩阵。
|me-a|=0,求得的m值即为a的特征值。|me-a|
是一个n次多项式,它的全部根就是n阶方阵a的全部特征值,这些根有可能相重复,也有可能是复数。
如果n阶矩阵a的全部特征值为m1
m2
...
mn,则|a|=m1*m2*...*mn
同时矩阵a的迹是特征值之和:tr(a)=m1+m2+m3+…+mn
如果n阶矩阵a满足矩阵多项式方程g(a)=0,
则矩阵a的特征值m一定满足条件g(m)=0;特征值m可以通过解方程g(m)=0求得。
还可用mathematica求得。
求解矩阵特征值及特征向量
矩阵特征值
定义1:设A是n阶矩阵,如果数 和n维非零列向量
和n维非零列向量 使关系式
使关系式 成立,则称这样的数
成立,则称这样的数 成为方阵A的特征值,非零向量
成为方阵A的特征值,非零向量 成为A对应于特征值
成为A对应于特征值 的特征向量。
的特征向量。
说明:1、特征向量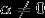 ,特征值问题是对方阵而言的。
,特征值问题是对方阵而言的。
2、n阶方阵A的特征值,就是使齐次线性方程组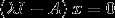 有非零解的
有非零解的 值,即满足方程
值,即满足方程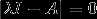 的
的 都是矩阵A的特征值。
都是矩阵A的特征值。
3、
定义2:A为n阶矩阵,称 为A的特征矩阵,其行列式
为A的特征矩阵,其行列式 为
为 的n次多项式,称为A的特征多项式,
的n次多项式,称为A的特征多项式,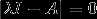 称为A的特征方程。
称为A的特征方程。
说明:1、由定义得, 是A的特征值,等价于
是A的特征值,等价于 是其特征方程
是其特征方程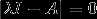 的根,因此又称
的根,因此又称 为A的特征根。若
为A的特征根。若 是
是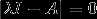 的
的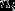 重根,则称
重根,则称 为A的
为A的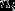 重特征值(根)。
重特征值(根)。
2、方程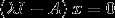 的任意非零解向量,都是对应于
的任意非零解向量,都是对应于 的特征向量。
的特征向量。
3、A的特征矩阵也可以表示为 ;
;
特征多项式也可以表示为 ;
;
特征方程也可以表示为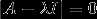 。
。
4、求A的特征值 就是求
就是求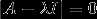 的根
的根 ,求A的相应于
,求A的相应于 的特征向量就是求
的特征向量就是求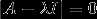 的非零解向量。
的非零解向量。
求矩阵A的特征值及特征向量问题就转化为求解多项式方程以及齐次线性方程组的通解问题。
下面是一些练习:
例 求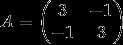 的特征值和特征向量
的特征值和特征向量
解 A的特征多项式为
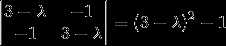
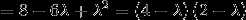
所以A的特征值为 ,
, 。
。
当 时,对应的特征向量应满足
时,对应的特征向量应满足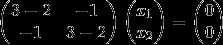 ,
,
即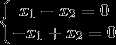
解得 ,所以对应的特征向量可取为
,所以对应的特征向量可取为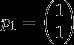 。故相应于
。故相应于![]() 的全体特征向量为
的全体特征向量为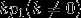
当 时,由
时,由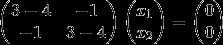 ,即
,即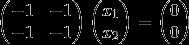 ,解得
,解得 ,所以对应的特征向量可取为
,所以对应的特征向量可取为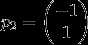 。故相应于
。故相应于 的全体特征向量为
的全体特征向量为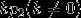
以上是关于矩阵的特征值求解的主要内容,如果未能解决你的问题,请参考以下文章