如何求函数的最小正周期？

Posted 2023-05-09

y=Asin(ωx+ψ)+B，(A≠0，ω＞0)其最小正周期为 ：T=2π/ω

如果一个函数f（x）的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f（x）的最小正周期。

拓展资料：

函数f(x)±g(x)最小正周期的求法

定义法

概念：根据周期函数和最小正周期的定义，确定所给函数的最小正周期。

例1、求函数y=|sinx|+|cosx|的最小正周期.

解:∵ =|sinx|+|cosx|

=|－sinx|+|cosx|

=|cos(x+π/2)|+|sin(x+π/2)|

=|sin(x+π/2)|+|cos(x+π/2)|

=f(x+π/2)

对定义域内的每一个x，当x增加到x+π/2时，函数值重复出现，因此函数的最小正周期是π/2.（如果f（x+T）=f（x），那么T叫做f（x）的周期）。

例2 、求函数

 

的最小正周期。

解：把

 

看成是一个新的变量z,那么2sinz的最小正周期是2π。

由于

 

。所以当自变量x增加到x+4π且必须增加到x+4π时，函数值重复出现。

∴函数

 

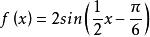
的最小正周期是4π。

百度百科-最小正周期

参考技术A

对于y=Asin(ωx+ψ)+B，(A≠0，ω＞0)其最小正周期为 ：T=2π/ω

函数的最小正周期，一般在高中遇到的都是特殊形式的函数，比如;f(a-x)=f(x+a),这个函数的最小周期就是T=(a-x+x+a)/2=a.还有那就是三角函数y=A sin(wx+b)+t，他的最小正周期就是T=2帕/w.

【拓展资料】

如果一个函数f(x)的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f(x)的最小正周期(minimal positive period).例如，正弦函数的最小正周期是2π.

根据上述定义，我们有:

对于正弦函数y=sinx, 自变量x只要并且至少增加到x+2π时，函数值才能重复取得正弦函数和余弦函数的最小正周期是2π。

y=Asin(ωx+φ), T=2π/ω(其中ω必须>0)

参考技术B 回答

y=Asin(ωx+ψ)或y=Acos(ωx+ψ)的最小正周期用公式计算：T=2π/ω。y=Atan(ωx+ψ)或y=cot(ωx+ψ)的最小正周期用公式计算：T=π/ω。对于正弦函数y=sinx, 自变量x只要并且至少增加到x+2π时，函数值才能重复取得正弦函数和余弦函数的最小正周期是2π。y=Asin(ωx+φ), T=2π/ω（其中ω必须>0）。

参考技术C 关于求三角函数最小正周期的问题，是三角函数的重点和难点，教科书和各种教参中虽有讲解，但其涉及到的题目类型及解决方法并不多，学生遇到较为复杂一点的问题时，往往不知从何入手。本文将介绍求三角函数最小正周期常用的五种方法，仅供参考。

一、定义法

直接利用周期函数的定义求出周期。
二、公式法

利用下列公式求解三角函数的最小正周期。

三、转化法

对较复杂的三角函数可通过恒等变形转化为 等类型，再用公式法求解
四、最小公倍数法

由三角函数的代数和组成的三角函数式，可先找出各个加函数的最小正周期，然后找出所有周期的最小公倍数即得。

注：

1. 分数的最小公倍数的求法是：（各分数分子的最小公倍数）÷（各分数分母的最大公约数）。

2. 对于正、余弦函数的差不能用最小公倍数法。
五、图像法

利用函数图像直接求出函数的周期。

这个只针对三角函数，一般求最小正周期也就求三角函数的！希望对你有帮助。 参考技术D

如果一个函数f（x）的所有周期中存在一个最小的正数，那么这个最小的正数就叫做f（x）的最小正周期（minimal positive period）.例如，正弦函数的最小正周期是2π [1]  .

根据上述定义，我们有：

对于正弦函数y=sinx, 自变量x只要并且至少增加到x+2π时，函数值才能重复取得正弦函数和余弦函数的最小正周期是2π。

y=Asin(ωx+φ), T=2π/ω（其中ω必须>0）

狄利克雷函数为什么不具有最小正周期

目录

• 一、狄利克雷函数
• 二、狄利克雷函数为什么是周期函数
• 三、狄利克雷函数为什么没有最小正周期

一、狄利克雷函数

狄利克雷（Dirichlet）函数如下所示：
\[ D(x) = \begincases 1,\quadx\inQ\,\,\,\,\quad(有理数-》可精确表示两个整数之比的数), \0,\quadx\inQ^C\quad(无理数-》不可精确表示两个整数之比的数), \endcases \]

二、狄利克雷函数为什么是周期函数

周期函数的定义：设函数\(f(x)\)的定义域为\(D\)，如果存在一个正数\(l\)，使得对于任一\(x\inD\)有\((x\pml)\inD\)且\(f(x+l)=f(x)\)，则称\(f(x)\)为周期函数，\(l\)称为\(f(x)\)的周期（通常指最小正周期）

判断狄利克雷函数为什么是周期函数之前，我们首先明确两件事（中学）：

1. \(有理数 + 正数 = 有理数\)
2. \(无理数 + 正数 = 无理数\)

如果理解了上述两件事，答案就出来了。从狄利克雷函数中，我们可以得知：只要\(x = 有理数\)，则\(f(x)=1\)；只要\(x=无理数\)，则\(f(x)=0\)，那任意一个正有理数（正数）r都可以是狄利克雷函数的周期。

三、狄利克雷函数为什么没有最小正周期

上文推出任意一个正有理数\(r\)都是狄利克雷函数的周期，由于不存在最小的正有理数，因此狄利克雷函数也就没有最小正周期。