社会网络分析-网络基本性质、中心性分析

Posted 2023-05-08

参考技术A 最近做了一些社会网络分析的工作，在这里写一个简单的总结。

这是一个专门用于复杂网络分析的包，执行pip install networkx即可安装。

网络中包含的节点个数。

网络中包含的边的个数。

网络中包含的边的个数占网络中所有可能的边的个数的比例。

也称为局部聚集系数，是网络中每个节点的聚集系数的平均值。节点的聚集系数为，将该节点的所有邻居两两组合，则共有 种组合，组合中的两个节点为邻居的组合数占所有组合数的比例即为该节点的聚集系数。

也称为全局聚集系数，即网络中的三角形结构占所有可能的三角形结构的比例。

互惠性是有向图的性质，即在有向图中，双向连接的边占所有边的比例。

中心性分析包括两方面，分别是节点的中心度和整体网络的中心势。

节点中心度包括三种，分别为度数中心度、接近中心度和中介中心度。

度数中心度是与某节点直接相连的其他节点的个数，如果一个点与许多点直接相连，那么该点具有较高的度数中心度。在有向图中，度数中心度分为出度中心度和入度中心度。由于这种测量仅关注与某一个节点直接相连的点数，忽略间接相连的点数，因此被视为局部中心度。

接近中心度是某个节点与图中所有其他点的最短距离之和的倒数，一个点越是与其他点接近，该点在传递信息方面就越不依赖其他节点，则该点就具有较高的接近中心度。在有向图中，接近中心度分为出接近中心度和入接近中心度。

中介中心度测量了某个节点在多大程度上能够成为“中间人”，即在多大程度上控制他人。如果一个节点处于多个节点之间，则可以认为该节点起到重要的“中介”作用，处于该位置的人可以控制信息的传递而影响群体。

上面描述的三种中心度的计算方法都是绝对中心度，绝对中心度有一个缺陷是，对于不同结构和规模的网络中的节点，其中心度无法直接进行比较，因此提出了相对中心度。相对中心度可以理解为是对绝对中心度进行了标准化。相对中心度的计算公式如下：

整体网络的中心势与节点的中心度相对应，也有三种，分别为度数中心势、接近中心势和中介中心势。

在networkx中定义了许多种网络，例如无向图、有向图、二分图、多层网络等等，这里我们使用有向图来做分析。

在这里我们初始化了一个有5个节点、6条边的有向图，注意，在给有向图添加边的时候，节点的顺序非常重要，第一个节点代表起点，第二个节点代表终点。

在network中可以直接计算网络的基本性质。

输出为：

在networkx中计算出来的中心度均为相对中心度。

输出为：

在networkx中没有似乎没有直接计算中心势的方法，这里我们可以根据公式自己计算。

输出为：

输出为：

当然，这个是最简单的画图方法了，networkx中还有更复杂的方法，可以根据自己的需要来进行个性化的处理。

以后有时间再写一下networkx画图~

ArcGIS 网络分析[1.5] 使用点线数据一起创建网络数据集（如何避免孤立点/点与线的连通性组合结果表）

ArcGIS中最基本的三种矢量数据是什么？点线面。

网络中除了路网之外，还会有地物点。

如上图，我们在建立网络数据集的时候，作为实验，当然可以只是公路网。但是在大型的决策任务中，网络数据集就不只是公路网那么简单了。

在城市与城市之间，有高速公路，国道，高铁，普铁，甚至还有水路。

如此复杂的网络模型是如何连通的呢？他们之间的交点又有什么样的连通方式呢？在这里，我仍然卖个关子，在以后的连通性一章，会详细说明。在文末，就会看到点作为网络数据集中十分强大而关键的一员出现，其意义是多连通组的时候，作为媒介，使得多组网络在其位置连通。

读者可以继续使用上几节提到的道路数据（修改后的），这节会新建一个点数据。

给个目录：

1. 点与线的拓扑关系

2. 用不同的点线连通方式创建网络数据集（读者可以一起操作，也可以直接看3的结论）

3. 单连通组中，点线连通策略不同而产生不同的结果

4. 什么样的点适合参与构建网络数据集

1. 点与线的拓扑关系

拓扑关系就是点与线的位置关系。

情况一：

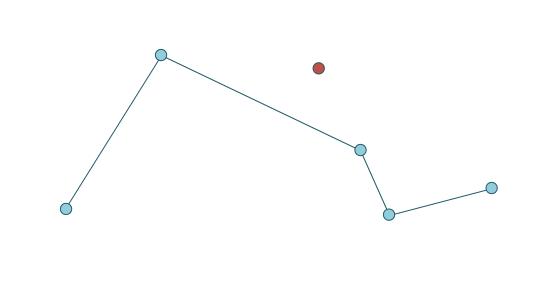
情况二：

 

情况三：

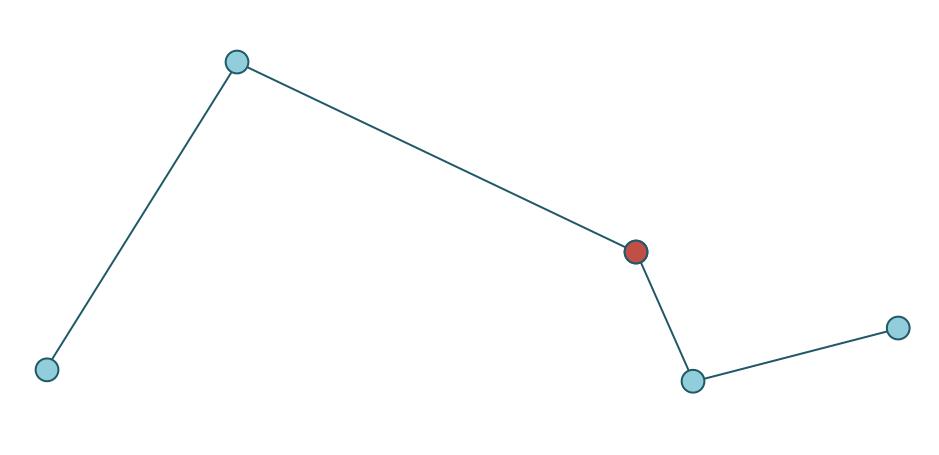
情况一是点是孤立点，上一节有说，即不在线上。

情况二，点在线上，却不在线的折点上。

情况三，点在线上，也在线的折点上。

——————假设在这里都是二维的道路，即高程=0———————

上一篇提到，前两种情况会产生孤立的点。

2. 用不同的点线连通方式创建网络数据集

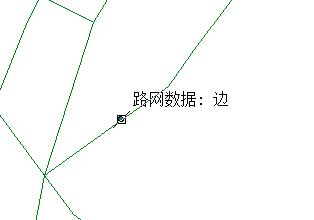
上两图为画点时开启捕捉的提示，我们分别在线外、线上、线折点上点一个点。

紫色为点，红绿色的是折线的折点。

创建网络数据集时，点的连通性就有了“依边线连通”、“交点处连通”两种选项：

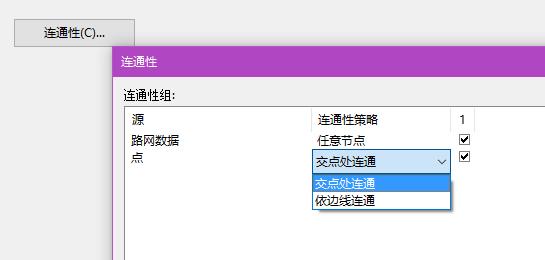
2.1 交点处连通（边线是按任意节点）

依边线连通就是“按照边线连通的方式来连通”。

构建完成后如上图提示，提示第一个点和第三个点是孤立的点。符合上文提及的三个情况。

网络数据集是这样的：

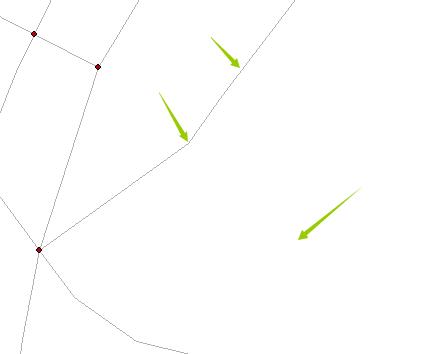
交汇点在网络数据集中是默认不显示的。（对网络数据集的图层进行符号显示-交汇点打勾，就能看到了）

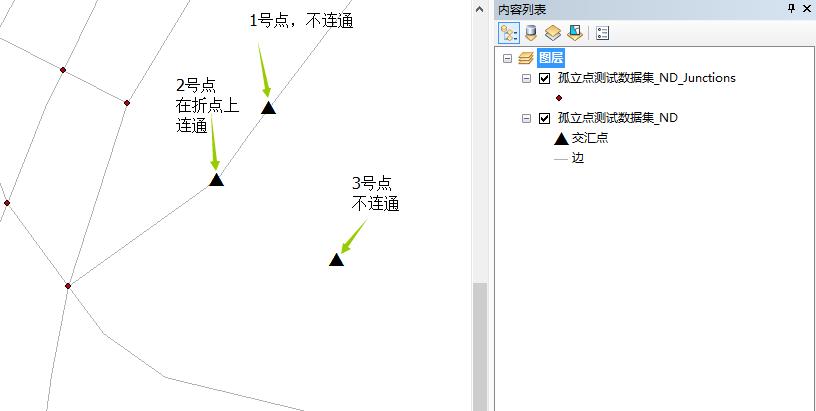
2.2 依边线连通（边线是按任意节点）

如果边线连通策略是“任意节点”，那么情况同2.1，如下图：

因为第二个点在边线的折点上。

如果边线连通连通策略是“端点”，那么：

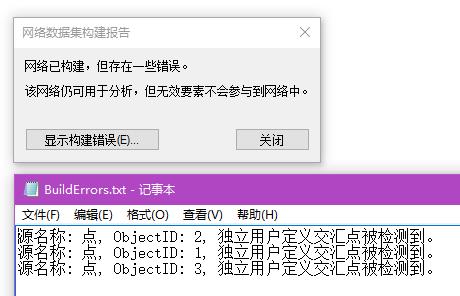
这样三个点都是孤立的点了，因为第二个点虽然在折点上，但是依旧被识别为独立的点。

原因就是第二个点不在折线的端点上，而点的连通策略是根据边线的连通策略定的——“依边线连通”。

2.3 假如组合方式是点【依边线连通】，线【任意节点】呢？

稍加思考，有点烧脑。

结果当然是第2个点连通，1、3点因为边线的连通策略，不在折点上而成为了孤立点。

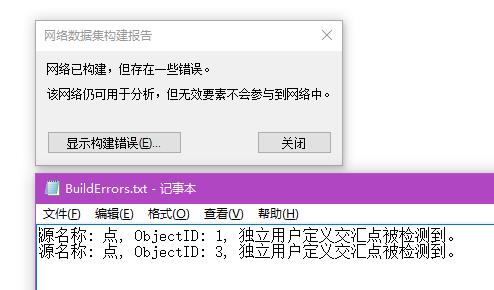
3. 所以点尽量还是画在边线的折点上（点在一个连通组中的不同情况）

如果不按标题行事

——画在了线外，那么肯定是孤立点

——画在了线上而不是折点上，那么非常大可能性还是孤立点

在网络数据集中，孤立点是很讨厌的一个东西，应该最大程度避免。

 

最后给出不同情况的点情况

A点在线外：必为孤立点，最好别参与网络数据集构建；

B点在线上：

——BA点不在线的折点上

　　此时无论连通性如何组合，点都为孤立点//解决方法：在点处编辑线，添加一个折点。

——BB点在线的折点上：

　　——BBA点在线的端点上：

　　　　组合方式：此时无论连通性如何组合，点不是孤立点。即该点处是连通的。

　　——BBB点在线的非端点折点上：

　　　　组合方式：线[端点]+点[任意]，点必为孤立点

　　　　　　　　　线[任意节点]+点[任意]，点不是孤立点，点处连通。

看文字太烦？看下面的网络图：

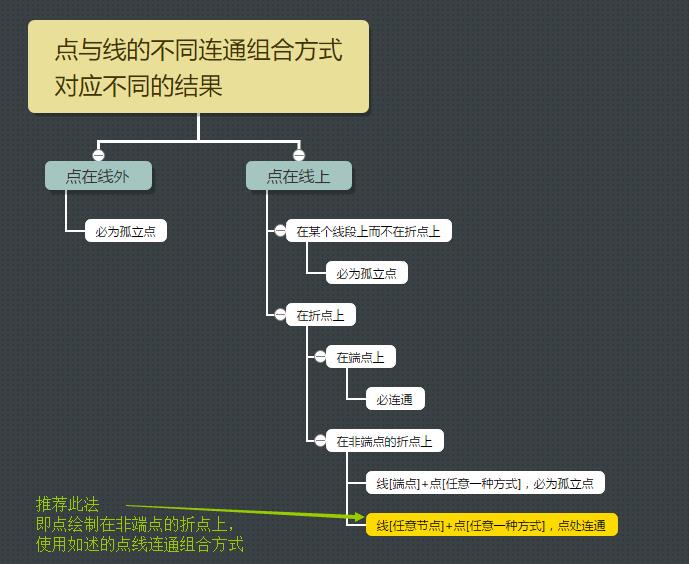
在实际地理事物中，道路曲曲折折很正常，直到下一个道路时才算结束一条折线。那么这条道路上就会有n个折点，这些折点有可能是交通路口等。

或许有读者想问了，如果我需要分析并不在道路上而在道路旁的位置（如公园），到另一个地方，那岂不是在公园点这个地方是孤立点？

我的提议就是，这种作为分析的点，必须将其绘制在线的折点上。

否则，就不要让其参与构建网络数据集，仅让它作为网络位置点即可。

 

因为孤立的点是无法到其他的位置的，也就是所谓的分析失败（见上一篇开头的错误提示截图）

4. 那么什么样的点合适参与网络数据集的构建呢？

在第四章，有多个连通性组的时候，点作为每一个不同的路网系统的中转媒介，就有着十分重要的作用。

到第四章，我就会详细介绍多连通性组的连通问题。这一篇博客和上一篇博客仅仅是热身。

【举个例子】

地铁站出口，既连通地铁网，又连通公路网。

公路网就不能与地铁网放在一个组里头了，不然小车会在交叉的地方开到轨道上吗？明显不现实。

但是又必须在地铁口处连通，使得人们方便换乘，那么地铁口就作为他们的连通点，连接着两个路网。