[机器学习] UFLDL笔记 - Convolutional Neural Network - 矩阵运算

Posted 2023-02-07 WangBo_NLPR

前言

　　卷积神经网络的核心操作就是各种矩阵运算，在前向传播和反向传播中的各种形式的矩阵运算构成了CNN的计算体系，本文将在卷积神经网络（Convolutional Neural Network）的背景下对相关的矩阵运算进行梳理，涉及矩阵乘积（matrix product）、元素对应乘积（element-wise product）、卷积操作（convolution）、相关操作和克罗内克积（kronecker product）等，在学习CNN的反向传播之前，我们必须先搞清楚这几种矩阵操作的计算过程，希望本文可以帮助大家理解卷积神经网络（CNN）提供一些帮助！

　　文章小节安排如下：
　　1）矩阵乘积（matrix product）
　　2）元素对应乘积（element-wise product）
　　3）卷积操作（convolution）
　　4）相关操作
　　5）克罗内克积（kronecker product）
　　6）总结
　　

一、矩阵乘积（matrix product）

1.1 矩阵乘积（matrix product）定义

　　矩阵的乘法运算不多说了，回顾一下最基本的定义：
　　设 A 为 m x p 的矩阵，B为 p x n 的矩阵，则称 C = AB 为矩阵A与B的乘积，且C为 m x n的矩阵，其中矩阵C中的第 i 行第 j 列元素可以表示为：

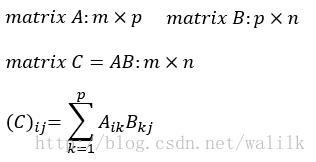
1.2 矩阵乘积的运算规律

　　分配律：A(B+B) = AB + AC
　　结合律：A(BC)=(AB)C
　　

二、元素对应乘积（element-wise product）

2.1 元素对应乘积（element-wise product）定义

　　元素对应乘积也称为Hadamard乘积（Hadamard product），矩阵A,B的Hadamard乘积定义为二者对应位置的乘积，也有人称作相关操作，记作：A⊙B
　　令C=A⊙B，则矩阵C中的第 i 行第 j 列元素可以表示为：
　　

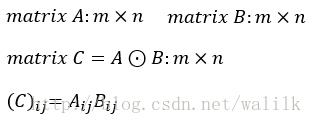
2.2 Hadamard乘积计算示意图 　　

　　Hadamard乘积的计算图示如下：

　　

2.3 Hadamard乘积的运算规律 　　

　　交换律：A⊙B=B⊙A
　　结合律：A⊙(B⊙C)=(A⊙B)⊙C
　　分配律：A⊙(B+C)=A⊙B+A⊙C

　　参考：
　　Hadamard product (matrices)
　　https://en.wikipedia.org/wiki/Hadamard_product_(matrices)
　　

三、卷积操作（convolution）

3.1 卷积操作（convolution）定义

　　卷积是一种应用非常广泛的数学计算方式，例如统计学、概率论、物理学、声学和计算机科学等。在一些领域比如信号与系统这门课中，卷积是基础理论，把卷积的概念弄清楚就可以很好的理解这门课中的其他概念了。正因为卷积在信号系统中的中哟啊行，所以很多文章都是从信号处理的角度来解释卷积。
　　图像也是一种信号，因此时间充裕的话，我也建议各位从信号系统的角度深入学习一下卷积概念，不仅要理解卷积的数学概念，同时也应该多关注卷积的物理意义，这样会非常有助于我们理解和研究深度学习算法。换句话说，我们不仅要知道CNN中的核心卷积操作是怎么计算的，还要知道从信号的角度分析，为什么卷积操作如此适用于CNN！

　　本文在这里只给出卷积操作在CNN中的定义，用于帮助理解CNN的反向传播和梯度计算（仅关注在数学上的计算过程）。关于卷积的更多知识，各位可以利用Google去学习。
卷积操作记作：A∗B
　　令c=A∗B，则实数值标量c可以表示为：

　　

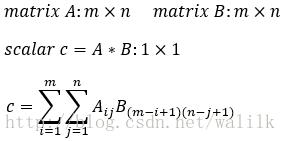
3.2 卷积操作计算示意图

　　卷积操作的计算示意图如下：

　　 卷积操作是CNN中的核心计算模式，在后面文章中会看到，CNN在反向传播中，误差的传递依靠的就是卷积操作，所以务必要搞清楚是怎么算的！
　　
　　参考：
　　如何通俗易懂解释卷积
　　 https://www.zhihu.com/question/22298352
　　

四、相关操作

4.1 相关操作定义

　　相关操作这个名称是在网上看到，具体的数学定义并没有查到，这里我就试着给出一个定义吧。
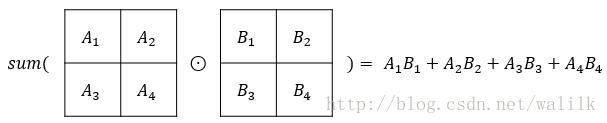
　　相关操作就是同型矩阵执行Hadamard乘积后再将所有元素相加（对应元素相乘将结果相加），得到一个实数值，符号可以记作：sum(A⊙B)
　　令c=sum(A⊙B)，则实数值标量c可以表示为：
　　

　　

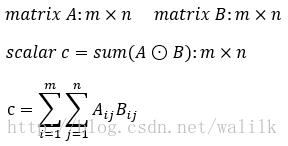
4.2 相关操作计算示意图

　　相关操作的计算示意图如下：
　　

　　

4.3 相关操作 or 卷积操作

　　在CNN的前向传播中，其实真正执行的是“相关操作”，而不是“卷积操作”，只是因为在具体实现时可以使用卷积的方式进行计算（A与B执行相关操作=A翻转180度以后再与B执行卷积操作），所以就使用了这样一个名字，所以CNN称为卷积神经网络。我们在这里一定要区分清楚CNN中的矩阵操作，但我们平时并不会过分强调到底是相关操作还是卷积操作，而是统一用“卷积”来描述，这有助于相互之间的交流（不必纠结细节）。
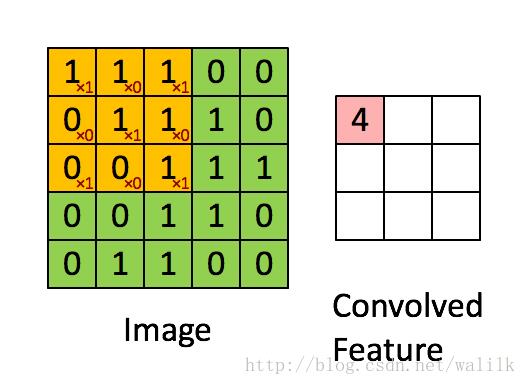
　　再来回顾一下经典的“卷积操作”：

　　

五、克罗内克积（kronecker product）

5.1 克罗内克积（kronecker product）定义

　　克罗内克积也是非常好理解的，这里就引用wiki百科的定义吧：
　　If A is an m × n matrix and B is a p × q matrix, then the Kronecker product A ⊗ B is the mp × nq block matrix:
　　

5.2 克罗内克积计算示意图

　　A is an m × n matrix and B is a p × q matrix, more explicitly of kronecker product:
　　

5.3 example

　　克罗内克积的计算示例：

　　

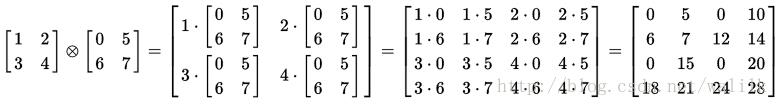
六、总结

　　矩阵运算是深度学习的重要基础，做深度学习基本就是在和各种矩阵打交道，前文只是在CNN的背景下对矩阵运算做了最基本的解释，并未深入探讨，如果想要深入研究深度学习，还死活建议抽出时间加强这方面的学习！！！
　　

参考文献

Hadamard product (matrices)
https://en.wikipedia.org/wiki/Hadamard_product_(matrices)
如何通俗易懂解释卷积
https://www.zhihu.com/question/22298352
Convolution
https://en.wikipedia.org/wiki/Convolution
Kronecker product
https://en.wikipedia.org/wiki/Kronecker_product