2022牛客多校3补题

Posted 2023-02-06 行码棋

2022牛客多校3补题

更好观感

A

给出两棵编号 $1-n$ 的树A和B，A和B树上每个节点均有一个权值，给出 $k$ 个关键点

的编号 $x_1\dots x_n$ ，问有多少种方案使得去掉恰好一个关键点使得剩余关键点在树A上

LCA的权值大于树B上LCA的权值

观察和不断模拟可以发现一系列的点的LCA可以通过前缀LCA实现。

故预处理出关键点序列的在树A B上的前缀LCA和后缀LCA，枚举去掉的关键节点并使用前后缀LCA算出剩余节点的LCA比较权值即可。

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
template <class T> void Min(T &a, const T b)  if (a > b) a = b; 
template <class T> void Max(T &a, const T b)  if (a < b) a = b; 
const int dx[] = -1, 0, 1, 0, dy[] = 0, 1, 0, -1;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
const ld eps = 1e-8;

struct Tree 
    std::vector<int> sz, top, dep, parent, in;
    int cur;
    std::vector<std::vector<int>> e;
    Tree(int n) : sz(n), top(n), dep(n), parent(n, -1), e(n), in(n), cur(0) 
    void addEdge(int u, int v) 
        e[u].push_back(v);
        e[v].push_back(u);
    
    void init() 
        dfsSz(0);
        dfsHLD(0);
    
    void dfsSz(int u) 
        if (parent[u] != -1)
            e[u].erase(std::find(e[u].begin(), e[u].end(), parent[u]));
        sz[u] = 1;
        for (int &v : e[u]) 
            parent[v] = u;
            dep[v] = dep[u] + 1;
            dfsSz(v);
            sz[u] += sz[v];
            if (sz[v] > sz[e[u][0]])
                std::swap(v, e[u][0]);
        
    
    void dfsHLD(int u) 
        in[u] = cur++;
        for (int v : e[u]) 
            if (v == e[u][0]) 
                top[v] = top[u];
             else 
                top[v] = v;
            
            dfsHLD(v);
        
    
    int lca(int u, int v) 
        while (top[u] != top[v]) 
            if (dep[top[u]] > dep[top[v]]) 
                u = parent[top[u]];
             else 
                v = parent[top[v]];
            
        
        if (dep[u] < dep[v]) 
            return u;
         else 
            return v;
        
    
;
void solve()

	int n, k;
	cin >> n >> k;
	vi x(k);
	for(int i = 0; i < k; i++)
	
		cin >> x[i];
		x[i]--;
	

	Tree A(n), B(n);
	vi a(n);
	for(int i = 0; i < n; i++)
		cin >> a[i];
	for(int i = 1; i < n; i++)
	
		int p;
		cin >> p;
		p--;
		A.addEdge(i, p);
	
	vi b(n);
	for(int i = 0; i < n; i++)
		cin >> b[i];
	for(int i = 1; i < n; i++)
	
		int p;
		cin >> p;
		p--;
		B.addEdge(i, p);
	
	A.init();
	B.init();

	vi prea(k), sufa(k), preb(k), sufb(k);
	for(int i = 0; i < k; i++)
	
		if(i == 0)
			prea[i] = preb[i] = x[i];
		else
		
			prea[i] = A.lca(prea[i - 1], x[i]);
			preb[i] = B.lca(preb[i - 1], x[i]);
		
	
	for(int i = k - 1; i >= 0; i--)
	
		if(i == k - 1)
			sufa[i] = sufb[i] = x[i];
		else
		
			sufa[i] = A.lca(sufa[i + 1], x[i]);
			sufb[i] = B.lca(sufb[i + 1], x[i]);
		
	
	int ans = 0;
	for(int i = 0; i < k; i++)
	
		if(i == 0)
		
			if(a[sufa[i + 1]] > b[sufb[i + 1]])
				ans++;
		
		else if(i == k - 1)
		
			if(a[prea[i - 1]] > b[preb[i -  1]])
				ans++;
		
		else
		
			int va = A.lca(prea[i - 1], sufa[i + 1]);
			int vb = B.lca(preb[i - 1], sufb[i + 1]);
			if(a[va] > b[vb])
				ans++;
		
	
	cout << ans << "\\n";


int main()

	ios::sync_with_stdio(false);
	cin.tie(0);

	int t;
	t = 1;
	// cin >> t;
	while(t--)
		solve();
	return 0;

C

题意： 给定n个字符串，求一个将他们拼接起来的方案，使得结果的字典序最小。

对$n$个字符串排序， $a$ 在 $b$ 前面的条件是 $a+b<b+a$

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 5, mod = 1e9 + 7;

void solve()

    int n;
    cin >> n;
    vector<string> s(n + 1);
    for(int i = 1; i <= n; i++)
        cin >> s[i];
    sort(s.begin() + 1, s.end(), [](string a, string b)
        return a + b < b + a;
    );
    for(int i = 1; i <= n; i++)
        cout << s[i];
    cout << "\\n";

int main()

    ios::sync_with_stdio(false);
    cin.tie(0);

    int t;
    // cin >> t;
    t = 1;
    while(t--)
        solve();
    return 0;

F

给定一个n个点m条边的无向图，每次询问两点x, y，求是否存在一个n的排列，使得第一个元素为x，最后一个元素为y，且排列的任意一个前缀、任意一个后

缀都连通

考虑一条链，那么两端的顶点是满足情况的，如果是其他的两个点那么不满足情况。

考虑一个环，发现环中的任意两个点都满足情况。

考虑一个图，图中可能存在环。

那么对所有的点双缩点之后，必须是一条链，如果不是一条链就不能满足。首先通过tarjan求出割点以及点双。

如果图本身就不连通（即有多个连通块），不满足。

如果点双等于1，即是一个环，满足。

接下来是对于一般的连通图，我们对于边界处的点双进行赋值，第一个边界处点双非割点全部赋为1，第二个边界处点双中非割点全部赋为2，那么询问时，如果两个点的值加和是3，即可以满足要求。

主要是如何判断是否是处于边界的点双，边界处的点双，那么此点双中的割点所在点双只有2个，不能有多个，如果有多个，必然不是在边界（因为存在一个割点至少则会存在两个点双）。

代码中为什么没有 $d=2$

因为存在以下情况：

上图是满足情况的，中间的点双连通分量的 $d=2$ ，但是边界1和6点都已经确定了，可以通过边界确定是否满足情况。

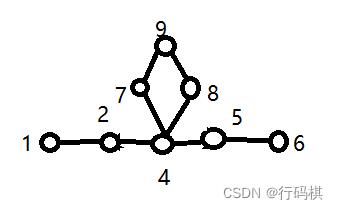
上图是不满足情况的，中间的点双中 $d=2$，但是边界也可以确定，同样可以通过边界来判断是否满足情况。

那么其他情况也是如此，都是可以通过边界点双连通分量来判断， $d=2$ 因为牵扯到有满足情况和不满足情况的，暂不考虑（但是他们可以通过边界点双来判断）

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
using ull = unsigned long long;
using db = double;
using ld = long double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;
using arr = array<int, 3>;
using vi = vector<int>;
using vl = vector<ll>;
template <class T> void Min(T &a, const T b)  if (a > b) a = b; 
template <class T> void Max(T &a, const T b)  if (a < b) a = b; 
const int dx[] = -1, 0, 1, 0, dy[] = 0, 1, 0, -1;
const int N = 1e5 + 5, M = N;
const int mod = 1e9 + 7;
const ld eps = 1e-8;

// sum[i] 是点i所在点双连通分量的个数
// ans[i] 是点i所在第几个边界的点双连通分量中
int low[N], dfn[N], stk[N], top, ts, dcc_cnt, root = 1, sum[N], ans[N];
vector<int> dcc[N], e[N];
bool cut[N];
void tarjan(int u)

	dfn[u] = low[u] = ++ts;
	stk[++top] = u;

	int flag = 0;
	for(auto v : e[u])
	
		if(!dfn[v])
		
			tarjan(v);
			low[u] = min(low[u], low[v]);
			if(dfn[u] <&
以上是关于2022牛客多校3补题的主要内容，如果未能解决你的问题，请参考以下文章
 
 2022牛客多校3补题
 2022牛客多校3补题
 2022牛客多校2补题
 2022牛客多校2补题
 2022牛客多校2补题
 2022牛客多校2补题