复数的运算法则

Posted 2023-04-30

（1）加法法则：复数的加法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，则它们的和是 (a+bi)+(c+di)=(a+c)+(b+d)i。

（2）减法法则：复数的减法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，则它们的差是 (a+bi)-(c+di)=(a-c)+(b-d)i。

（3）乘法法则：规定复数的乘法按照以下的法则进行：设z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积(a+bi)(c+di)=(ac-bd)+(bc+ad)i。

（4）除法法则：复数除法定义：满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。

运算方法：可以把除法换算成乘法做，在分子分母同时乘上分母的共轭.。所谓共轭你可以理解为加减号的变换，互为共轭的两个复数相乘是个实常数。

扩展资料：

复数的运算律

（1）加法交换律：z1+z2=z2+z1

（2）乘法交换律：z1×z2=z2×z1

（3）加法结合律：(z1+z2)+z3=z1+(z2+z3)

（4）乘法结合律：(z1×z2)×z3=z1×(z2×z3)

（5）分配律：z1×(z2+z3)=z1×z2+z1×z3

参考资料：百度百科-复数运算法则

参考技术A

加法法则
复数的加法法则：设z1=a+bi,z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。两个复数的和依然是复数。
即
乘法法则
复数的乘法法则：把两个复数相乘，类似两个多项式相乘，结果中i²= -1，把实部与虚部分别合并。两个复数的积仍然是一个复数。
即
除法法则
复数除法定义：满足 的复数 叫复数a+bi除以复数c+di的商。
运算方法：将分子和分母同时乘以分母的共轭复数，再用乘法法则运算，
即
开方法则
若z^n=r(cosθ+isinθ），则
z=n√r[cos(2kπ+θ）/n+isin(2kπ+θ）/n]（k=0，1，2，3……n-1）
运算律
加法交换律：z1+z2=z2+z1
乘法交换律：z1*z2=z2*z1
加法结合律：(z1+z2)+z3=z1+(z2+z3)
乘法结合律：(z1*z2)*z3=z1*(z2*z3)
分配律：z1*(z2+z3)=z1*z2+z1*z3
i的乘方法则
i^(4n+1)=i, i^(4n+2)=-1, i^(4n+3)=-i, i^4n=1（其中n∈Z）
棣莫佛定理
对于复数z=r(cosθ+isinθ），有z的n次幂
z^n=(r^n)*[cos(nθ）+isin(nθ）]　（其中n是正整数）
复数三角形式
设复数z1、z2的三角形式分别为r1(cosθ1+isinθ1）和r2(cosθ2+isinθ2），那么z1z2=r1r2[cos（θ1+θ2)+isin（θ1+θ2)]（在复数平面内为模相乘，角相加。）
z1÷z2=(r1÷r2)[cos（θ1－θ2)+isin（θ1－θ2)]（在复数平面内为模相除，角相减。）
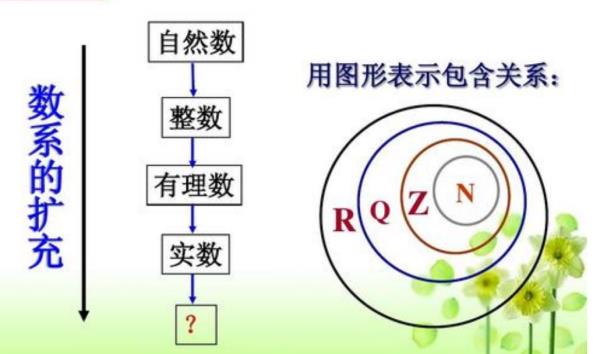
复数集不同于实数集的几个特点是：开方运算永远可行（不包括纯虚数集）
一元n次复系数方程总有n个根（重根按重数计）；复数不能建立大小顺序。

参考技术B

负数的运算包括加法法则，乘法法则，除法法则，开方法则，运算律，i的乘方法则等。具体运算方法如下：

1.加法法则

复数的加法法则：设z1=a+bi，z2=c+di是任意两个复数。两者和的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。两个复数的和依然是复数。即

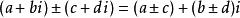
2.乘法法则

复数的乘法法则：把两个复数相乘，类似两个多项式相乘，结果中i2= -1，把实部与虚部分别合并。两个复数的积仍然是一个复数。即

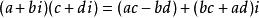
3.除法法则

复数除法定义：满足

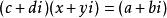 的复数

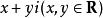 叫复数a+bi除以复数c+di的商。

运算方法：将分子和分母同时乘以分母的共轭复数，再用乘法法则运算，

即

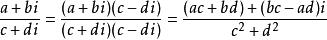
4.开方法则

若zn=r(cosθ+isinθ），则

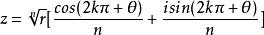
（k=0，1，2，3…n-1）

5.运算律

加法交换律：z1+z2=z2+z1

乘法交换律：z1×z2=z2×z1

加法结合律：(z1+z2)+z3=z1+(z2+z3)

乘法结合律：(z1×z2)×z3=z1×(z2×z3)

分配律：z1×(z2+z3)=z1×z2+z1×z3

6.i的乘方法则

i4n+1=i, i4n+2=-1, i4n+3=-i, i4n=1（其中n∈Z）

7.棣莫佛定理

对于复数z=r(cosθ+isinθ），有z的n次幂

zn=rn[cos(nθ)+isin(nθ)]　（其中n是正整数）

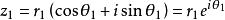
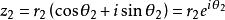
则

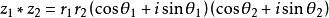
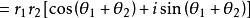
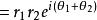
扩展资料

共轭复数释义

对于复数

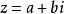
称之为复数

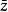
=a-bi为z的共轭复数。即两个实部相等，虚部互为相反数的复数互为共轭复数(conjugate complex number）。复数z的共轭复数记作

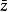
性质

根据定义，若

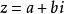
(a，b∈R），则

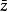=a－bi（a,b∈R）。共轭复数所对应的点关于实轴对称。两个复数：x+yi与x-yi称为共轭复数，它们的实部相等，虚部互为相反数。

在复平面上，表示两个共轭复数的点关于X轴对称，而这一点正是"共轭"一词的来源----两头牛平行地拉一部犁，它们的肩膀上要共架一个横梁，这横梁就叫做"轭"。如果用z表示x+yi，那么在z字上面加个"一"就表示x-yi，或相反。

共轭复数有些有趣的性质：

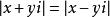
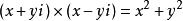
参考资料来源：百度百科-复数

参考技术C

1、加法法则

复数的加法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，

则它们的和是 (a+bi)+(c+di)=(a+c)+(b+d)i。

两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

2、减法法则

复数的减法按照以下规定的法则进行：设z1=a+bi，z2=c+di是任意两个复数，

则它们的差是 (a+bi)-(c+di)=(a-c)+(b-d)i。

两个复数的差依然是复数，它的实部是原来两个复数实部的差，它的虚部是原来两个虚部的差。

3、乘法法则

规定复数的乘法按照以下的法则进行：

设z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积(a+bi)(c+di)=(ac-bd)+(bc+ad)i。

其实就是把两个复数相乘，类似两个多项式相乘，展开得: ac+adi+bci+bdi2，因为i2=-1，所以结果是(ac－bd)+(bc+ad)i 。两个复数的积仍然是一个复数。

4、除法法则

复数除法定义：满足(c+di)(x+yi)=(a+bi)的复数x+yi(x,y∈R)叫复数a+bi除以复数c+di的商。

运算方法：可以把除法换算成乘法做，在分子分母同时乘上分母的共轭.。所谓共轭你可以理解为加减号的变换，互为共轭的两个复数相乘是个实常数。

扩展资料

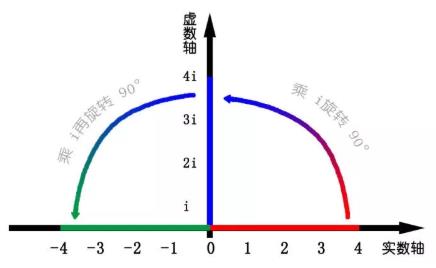
复数的加法就是自变量对应的平面整体平移，复数的乘法就是平面整体旋转和伸缩，旋转量和放大缩小量恰好是这个复数对应向量的夹角和长度。

二维平移和缩放是一维左右平移伸缩的扩展，旋转是一个至少要二维才能明显的特征，限制在一维上，只剩下旋转0度或者旋转180度，对应于一维导数正负值（小线段是否反向）。

参考资料来源：百度百科-复数运算法则

参考技术D

复数运算法则有：加减法、乘除法。两个复数的和依然是复数，它的实部是原来两个复数实部的和，它的虚部是原来两个虚部的和。

复数的加法满足交换律和结合律。此外，复数作为幂和对数的底数、指数、真数时，其运算规则可由欧拉公式e^iθ=cos θ+i sin θ（弧度制）推导而得。

扩展资料：

规定复数的乘法按照以下的法则进行：

设z1=a+bi，z2=c+di(a、b、c、d∈R)是任意两个复数，那么它们的积(a+bi)(c+di)=(ac-bd)+(bc+ad)i。

其实就是把两个复数相乘，类似两个多项式相乘，展开得: ac+adi+bci+bdi2，因为i2=-1，所以结果是(ac－bd)+(bc+ad)i 。两个复数的积仍然是一个复数。

在极坐标下，复数可用模长r与幅角θ表示为(r,θ)。对于复数a+bi,r=√(a²+b²)，θ=arctan(b/a)。此时，复数相乘表现为幅角相加，模长相乘。

java 中实现复数的加减

题目如下： 定义一个复数类，该类包含实部和虚部属性及构造函数。类中还应包含实现复数加法、减法、乘法的方法。并在程序中使用这个类。

（1）：具体代码(附注释)

复数类：

public class Complex 

private float shibu;

private float xubu;

Complex()

this(0,0);

Complex(float shibu,float xubu)

this.shibu=shibu;

this.xubu=xubu;

public void Add(Complex p)

Complex result=new Complex();

result.shibu=this.shibu+p.shibu;

result.xubu=this.xubu+p.xubu;

System.out.print("加法结果为:"+result.shibu+"+"+result.xubu+"i");

public void Sub(Complex p)

Complex result=new Complex();

result.shibu=this.shibu-p.shibu;

result.xubu=this.xubu-p.xubu;

System.out.print("加法结果为:"+result.shibu+"+"+result.xubu+"i");

public void Mul(Complex p)

Complex result=new Complex();

result.shibu=this.shibu*p.shibu-this.xubu*p.xubu;

result.xubu=this.shibu*p.xubu+p.shibu*this.xubu;

System.out.print("乘法结果为:"+result.shibu+"+"+result.xubu+"i");

public static void main(String[] args) 

Complex fushu1=new Complex(1,2);

Complex fushu2=new Complex(3,4);

fushu1.Add(fushu2);

fushu1.Sub(fushu2);

fushu1.Mul(fushu2);

（2）：提供一个例子：

源代码：

import java.io.*;

public class Book

double sb;

double xb;

Book(double x,double y)

this.sb=x;

this.xb=y;

Book()

   

public static void main(String args[])

System.out.println("请输入数据：");

double a=0;

double b=0;

double c=0;

double d=0;

String s;

BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

System.out.println("请输入第一个复述的实部：");

try

s = in.readLine();

a=Double.parseDouble(s);

catch(IOException e)

 System.out.println("抛掷异常");

System.out.println("请输入第一个复述的虚部：");

try

s = in.readLine();

b =Double.parseDouble(s);

catch(IOException e)

 System.out.println("抛掷异常");

System.out.println("请输入第二个复述的实部：");

try

s = in.readLine();

c =Double.parseDouble(s);

catch(IOException e)

 System.out.println("抛掷异常");

System.out.println("请输入第二个复述的虚部：");

try

s = in.readLine();

d =Double.parseDouble(s);

catch(IOException e)

 System.out.println("抛掷异常");

Book h;

h=new Book(a,b);

Book j;

j=new Book(c,d);

System.out.println("您输入的一个数为：");

toString(h);

System.out.println("您输入的二个数为：");

toString(j);

Book k;

k=new Book();

char z=\'y\';

do

System.out.println("请选择您要进行的计算：");

System.out.println("1 ：进行加法运算");

System.out.println("2 ：进行减法运算");

System.out.println("3 ：进行修改");

System.out.println("4 ：进行乘法运算");

System.out.println("5 ：进行除法运算");

System.out.println("6 ：查看修改结果");

int i=0;

try

i= Integer.parseInt(in.readLine());

catch(IOException e)

 System.out.println("抛掷异常");

switch(i)

case 1:

k.sb=jia(h.sb,j.sb);

k.xb=jia(h.xb,j.xb);

System.out.println("计算结果的实部为："+k.sb);

System.out.println("计算结果的虚部为："+k.xb);

toString(k);

break ;

case 2:

k.sb=jian(h.sb,j.sb);

k.xb=jian(h.xb,j.xb);

System.out.println("计算结果的实部为："+k.sb);

System.out.println("计算结果的虚部为："+k.xb);

toString(k);

break ;

case 3:

System.out.println("请输入您要修改哪个实数：");

int l=0;

try

l= Integer.parseInt(in.readLine());

catch(IOException e)

 System.out.println("抛掷异常");

if(l==1)

h.xiugais(h);

h.xiugaix(h);

else

xiugais(j);

xiugaix(j);

break ;

case 4:

double f=0;

double e=0;

f=cheng(h.sb,j.sb)+cheng(h.xb,j.xb);

e=cheng(h.sb,j.xb)+cheng(h.xb,j.sb);

k.sb=(double)(Math.round(f*100)/100.0);

k.xb=(double)(Math.round(e*100)/100.0);

System.out.println("计算结果的实部为："+k.sb);

System.out.println("计算结果的虚部为："+k.xb);

toString(k);

break ;

case 5:

double chushu=cheng(j.sb,j.sb)-cheng(j.xb,-j.xb);

double beichushus=jian(cheng(h.sb,j.sb),cheng(h.xb,-j.xb));

double beichushux=jia(cheng(h.sb,-j.xb),cheng(h.xb,j.sb));

k.sb=chu(beichushus,chushu);

k.xb=chu(beichushux,chushu);

System.out.println("计算结果的实部为："+k.sb);

System.out.println("计算结果的虚部为："+k.xb);

toString(k);

break ;

case 6:

System.out.println("修改后的结果为：");

System.out.println("第一个复数："+toString(h));

System.out.println("第二个复数："+toString(j));

break ;

System.out.println("请问您是否还要继续 y/n：");

try

z=(char)System.in.read();

System.in.skip(2); //忽略回车换行

catch(IOException e)

 while(z==\'y\');

public static double gets(Book a)

return a.sb;

public static double getx(Book b)

return b.xb;

public static double xiugais(Book a)

BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

System.out.println("请输入您要修改的实部：");

double m=0;

try

m= Double.parseDouble(in.readLine());

catch(IOException e)

 System.out.println("抛掷异常");

a.sb=m;

System.out.println("修改成功：");

return 0;

public static double xiugaix(Book b)

BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

System.out.println("请输入您要修改的虚部：");

double n=0;

try

n= Double.parseDouble(in.readLine());

catch(IOException e)

 System.out.println("抛掷异常");

b.xb=n;

System.out.println("修改成功：");

return 0;

public static double jia(double a,double b)//

double c=0;

c=a+b;

System.out.println("加法成功：");

return c ;

public static double jian(double a,double b)

double c=0;

c=a-b;

System.out.println("减法成功：");

return c;

public static double cheng(double a,double b)

double c=0;

c=a*b;

System.out.println("乘法成功：");

return  c;

public static double chu(double a,double b)

double d=0;

double c=0;

d=a/b;

c=(double)(Math.round(d*100)/100.0);

System.out.println("除法成功：");

return c ;

public  static double toString(Book a)

System.out.println("结果为："+a.sb+"+"+a.xb+"*i");

return 0;

（3）测试结果截图：

参考技术A 不知道是不是 ～
//复数类。

public class Complex

private double real,im; //实部，虚部

public Complex(double real, double im) //构造方法

this.real = real;
this.im = im;


public Complex(double real) //构造方法重载

this(real,0);


public Complex()

this(0,0);


public Complex(Complex c) //拷贝构造方法

this(c.real,c.im);


public boolean equals(Complex c) //比较两个对象是否相等

return this.real==c.real && this.im==c.im;


public String toString()

return "("+this.real+"+"+this.im+"i)";


public void add(Complex c) //两个对象相加
//改变当前对象，没有返回新对象
this.real += c.real;
this.im += c.im;


public Complex plus(Complex c) //两个对象相加，与add()方法参数一样不能重载
//返回新创建对象，没有改变当前对象
return new Complex(this.real+c.real, this.im+c.im);


public void subtract(Complex c) //两个对象相减
//改变当前对象，没有返回新对象
this.real -= c.real;
this.im -= c.im;


public Complex minus(Complex c) //两个对象相减，与subtract()方法参数一样不能重载
//返回新创建的对象，没有改变当前对象
return new Complex(this.real-c.real, this.im-c.im);



class Complex__ex

public static void main(String args[])

Complex a = new Complex(1,2);
Complex b = new Complex(3,5);
Complex c = a.plus(b); //返回新创建对象
System.out.println(a+" + "+b+" = "+c);



/*
程序运行结果如下：
(1.0+2.0i) + (3.0+5.0i) = (40.0+7.0i)

*/