LeetCode 1129颜色交替的最短路径广度优先HERODING的LeetCode之路

Posted 2023-02-02 HERODING23

解题思路：
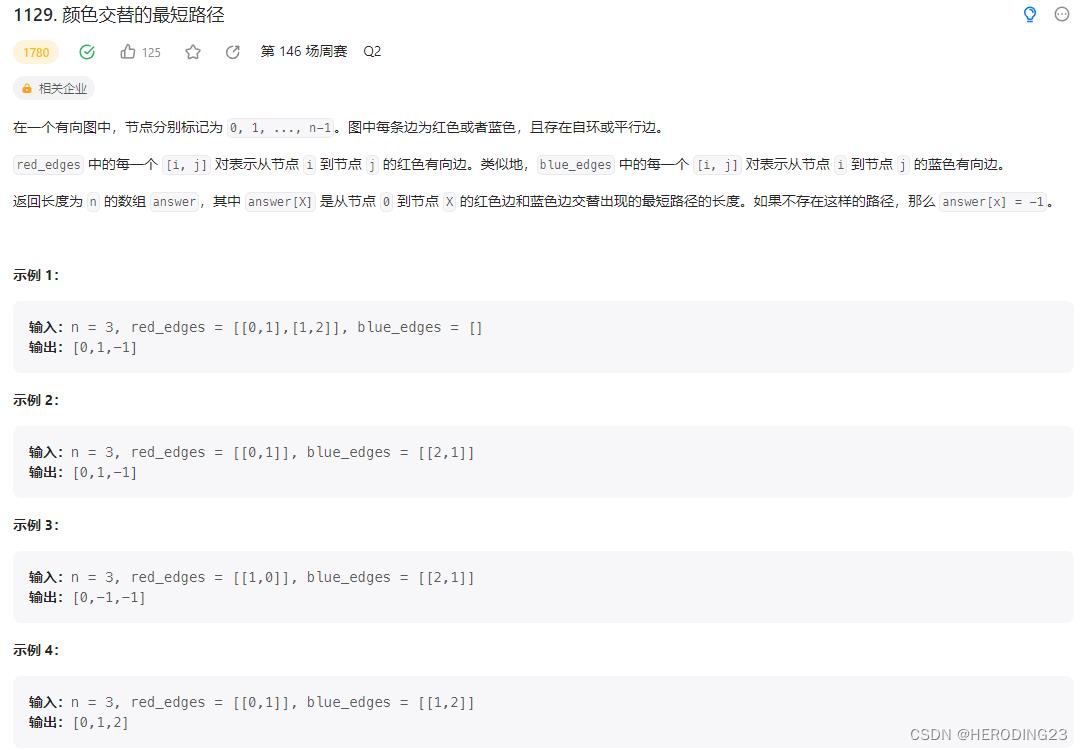
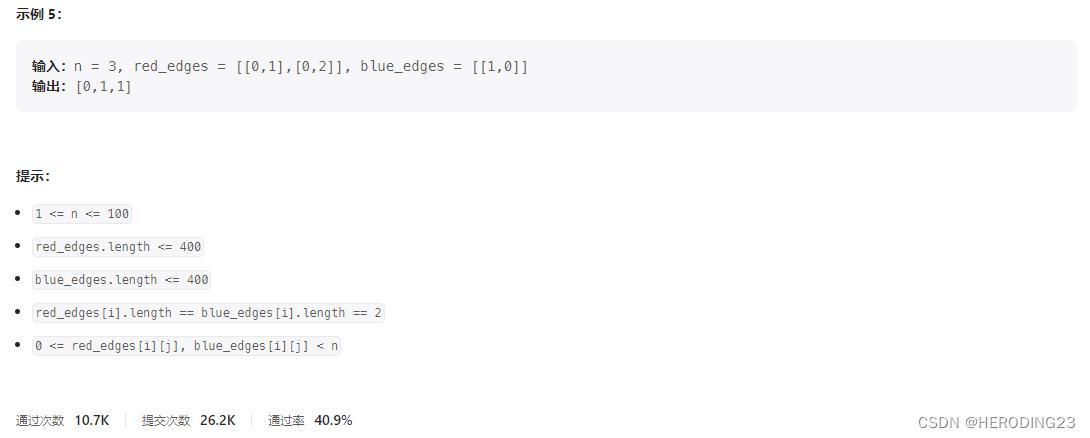
一道非常有意思的广度优先遍历问题，一般的优先遍历问题，即可以广度优先遍历，也可以深度优先遍历，甚至动态规划求解，但是这里并不是求单一最优解问题，也不是按照顺序去执行的，所以深度优先和动态规划不太适用。这道题最有意思的地方在于，有向连接是有颜色区分的，也就是说，在构建邻接矩阵时，要考虑颜色的不同，同时红蓝相间连接表明要不断交替遍历红邻接矩阵和蓝邻接矩阵，红先红后两种情况都要考虑，剩下的就是简单的广度优先模板了，只不过要执行两遍罢了。步骤如下：

1. 构建红蓝邻接矩阵；
2. 构建dist数组，初始化队列；
3. 从零节点开始红蓝相间遍历，更新dist数组；
4. 遍历dist数组，选择红先蓝先最小的距离；

代码如下：

class Solution 
public:
    vector<int> shortestAlternatingPaths(int n, vector<vector<int>>& redEdges, vector<vector<int>>& blueEdges) 
        // 构建邻接矩阵
        vector<vector<int>> red(n);
        vector<vector<int>> blue(n);
        for(auto& redEdge : redEdges) 
            red[redEdge[0]].emplace_back(redEdge[1]);
        
        for(auto& blueEdge : blueEdges) 
            blue[blueEdge[0]].emplace_back(blueEdge[1]);
        
        // 记录不同颜色最短路径
        vector<vector<int>> dist(2, vector<int>(n, INT_MAX));
        // 队列
        queue<pair<int, int>> q;
        // 零点初始化
        dist[0][0] = 0;
        dist[1][0] = 0;
        // 零点入队列(类型、顶点)
        q.push(0, 0);
        q.push(1, 0);
        while(!q.empty()) 
            auto [t, index] = q.front();
            q.pop();
            // 如果是红色
            if(t == 0) 
                for(auto& b : blue[index]) 
                    if(dist[1 - t][b] == INT_MAX) 
                        dist[1 - t][b] = dist[t][index] + 1;
                        q.push(1 - t, b);
                     else continue;
                
             else  // 如果是蓝色
                for(auto& r : red[index]) 
                    if(dist[1 - t][r] == INT_MAX) 
                        dist[1 - t][r] = dist[t][index] + 1;
                        q.push(1 - t, r);
                     else continue;
                
            
        
        vector<int> res(n);
        for(int i = 0; i < n; i ++) 
            res[i] = min(dist[0][i], dist[1][i]);
            if(res[i] == INT_MAX) 
                res[i] = -1;
            
        
        return res;
    
;