ZJCPC2022 第19届 浙江省赛The 19th Zhejiang Provincial Collegiate Programming Contest(CBALGMIF 8题)
Posted 小哈里
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了ZJCPC2022 第19届 浙江省赛The 19th Zhejiang Provincial Collegiate Programming Contest(CBALGMIF 8题)相关的知识,希望对你有一定的参考价值。
文章目录
补题链接:https://codeforces.com/gym/103687
C.JB Wants to Earn Big Money

题意:
- 有 n 个人想买一些股票,m 个人想卖一些股票。每个人都会给出一个价格。
- 系统将确定最终价格 x。对于想买一些股票的人,如果他给出的价格不低于x,他就会加入交易。对于想卖掉部分股份的人,如果他给出的价格不高于x,他就会加入交易。
- 求可以加入交易的人数。
思路:
- 扫一遍序列,判断是否满足条件即可。
#include<bits/stdc++.h>
using namespace std;
int main()
int n, m, x; cin>>n>>m>>x;
int res = 0;
for(int i = 1; i <= n; i++)
int t; cin>>t; res += (t>=x);
for(int i = 1; i <= m; i++)
int t; cin>>t; res += (t<=x);
cout<<res<<"\\n";
return 0;
B.JB Loves Comma

题意:
- 给你一个字符串s,让你在每个cjb子串的后面添加一个逗号后输出。
思路:
- 直接扫一遍, 在每个cjb后面输出,即可。
#include<bits/stdc++.h>
using namespace std;
int main()
string s; cin>>s;
cout<<s[0]<<s[1];
for(int i = 2; i < s.size(); i++)
cout<<s[i];
if(s[i]=='b' && s[i-1]=='j' && s[i-2]=='c')cout<<',';
return 0;
A.JB Loves Math

题意:
- 给出两个整数a和b,然后你应该选择一个正奇数 x 和一个正偶数 y(不能更改x和y的值)。
- 你可以在一次操作中让 a 加 x 或让 a 减 y。求将 a 更改为 b 所需的最少操作数。
思路:
- 题目等价于让a变成b,可以增加奇数,或者减少偶数。显然次数不超过三次,分类讨论即可。
- a小于b
(b-a)为奇数,那么1次
(b-a)/2为偶数,那么2次(b-a)/2
(b-a)/2为奇数,那么3次。 - a大于b
(a-b)为偶数,那么1次
(a-b)为奇数,那么2次。增加一,再减去(a-b+1)
#include<bits/stdc++.h>
using namespace std;
int main()
int T; cin>>T;
while(T--)
int a, b; cin>>a>>b;
if(a==b)cout<<"0\\n";
else if(a<b)
int t = b-a;
if(t%2==1)cout<<"1\\n";
else if(t/2%2==1)cout<<"2\\n";
else cout<<"3\\n"; //1,2,3
else
int t = a-b;
if(t%2==0)cout<<"1\\n";
else cout<<"2\\n";
return 0;
L.Candy Machine

题意:
- 给出n个整数(1e9),从中选出若干个,满足这些数中严格大于它们的平均值的数的个数最多。
- 求最多能选出多少个整数。
思路:
- 假设最终选择的集合的平均数不超过k,为使平均数不超过 k,应将 ≤ k 的数全部选入,然后贪心选择 > k 的部分中最小的若干个数。
- 因此将 N 个数从小到大排序后,最优解一定是一个前缀。
- 枚举每个前缀,二分统计严格大于平均数的数字个数。时间复杂度nlogn。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
int a[N];
int main()
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n; cin>>n;
for(int i = 1; i <= n; i++)cin>>a[i];
sort(a+1,a+n+1);
int res = 0;
double pre = 0, avg;
for(int i = 1; i <= n; i++)
pre += a[i];
avg = pre/i;
int l = 0, r = i;
while(l < r)
int mid = l+r+1>>1;
if(a[mid]<=avg*1.0)l = mid;
else r = mid-1;
res = max(res, i-r);
cout<<res<<"\\n";
return 0;
G.Easy Glide

题意:
- 给定二维平面上 n 个(1000)滑行点。已知行走速度为V1,每次经过某个滑行点后可以按V2速度滑行 3 秒。
- 求从 起点S 滑行到 终点T 所需的最少时间。
思路:
- 建立一张 n + 2 个点的有向图,分别表示 n 个滑行点以及起点 S 和终点 T。
- 由起点向每个点连单向边,边权为 S 按 V1 走到至该点所需的时间。
- 由每个滑行点向其它滑行点以及终点连单向边,边权为先按V2 滑行至多 3 秒然后按 V1 行走至目的地所需的时间。
- 朴素 Dijkstra 求 S 到 T 的最短路。
- 复杂度O(n^2)
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int>PII;
#define x first
#define y second
const int N = 1010;
int n, v1, v2;
PII a[N];
double e[N][N];
double get_dist(PII x, PII y) return hypot(x.x-y.x, x.y-y.y)/v1; ;
double get_dist2(PII x, PII y)
double d1 = hypot(x.x-y.x, x.y-y.y);
return d1<=v2*3? d1/v2 : 3+(d1-v2*3)/v1;
double dist[N];
int vis[N];
double dijkstra()
memset(dist, 0x42, sizeof dist);
dist[0] = 0;
for(int i = 1; i <= n; i++)
int t = -1;
for(int j = 0; j <= n; j++)
if(!vis[j] && (t==-1 || dist[t]>dist[j]))t = j;
vis[t] = 1;
for(int j = 1; j <= n; j++)
dist[j] = min(dist[j], dist[t]+e[t][j]);
return dist[n];
void solve()
cin>>n;
for(int i = 1; i <= n; i++)cin>>a[i].x>>a[i].y;
n++;
cin>>a[0].x>>a[0].y>>a[n].x>>a[n].y;
cin>>v1>>v2;
memset(e, 0x42, sizeof(e));
for(int i = 1; i <= n; i++)
e[0][i] = get_dist(a[0], a[i]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i==j)continue;
e[i][j] = get_dist2(a[i], a[j]);
cout<<fixed << setprecision(12) << dijkstra()<<"\\n";
int main()
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T = 1; //cin>>T;
while(T--)
solve();
return 0;
M.BpbBppbpBB
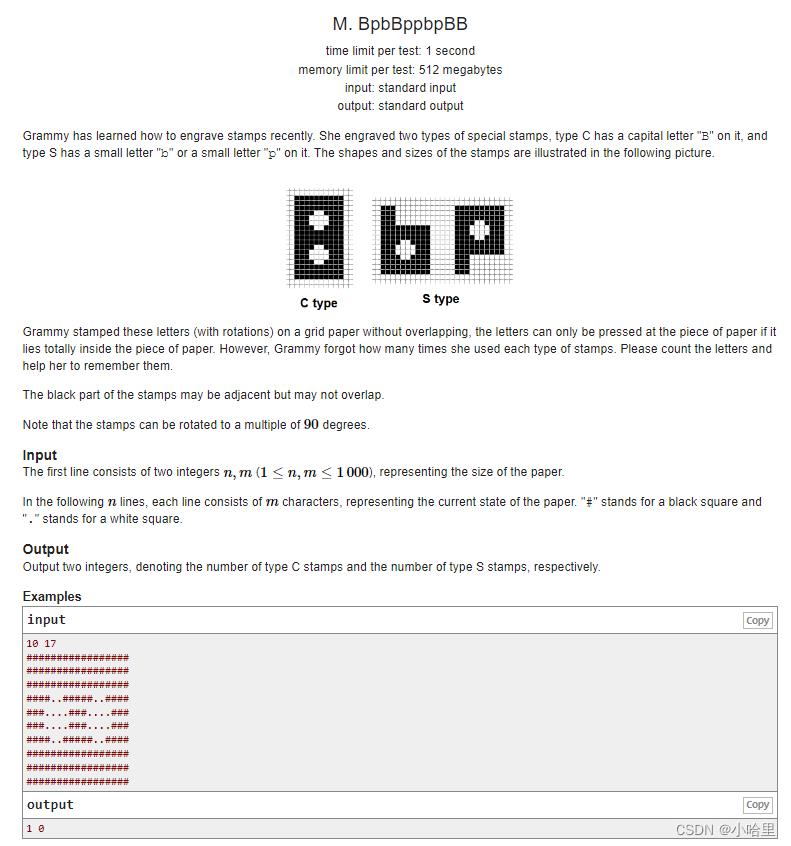
题意:
- 给定使用两种印章无重叠可旋转地打印出的字符画,统计每种印章的使用次数。
思路:
题解做法:
- C型的黑格子数为146,S型的黑格子数为100。
- 假设两种印章分别使用了 x 个和 y 个。
则黑格子数为146 x + 100 y, 洞数为2 x + y, 联立解方程即可。- 考虑如何统计洞数,从上往下、从左往右扫一遍字符矩阵,遇到白格子时做一遍DFS,统计每个连通块中白格子的个数,若为12,检查该白格子的附近是否满足洞的特征。
- 更方便的做法,直接找出所有的洞的个数。对于两个洞,如果中间相差的距离为7,那么就是C型(因为S拼起来肯定是>7的),那么剩下的就是S啦。
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
char a[N][N];
int dx[] = 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3;
int dy[] = 0, 1, -1, 0, 1, 2, -1, 0, 1, 2, 0, 1;
int check(int x, int y)
if(x-1 < 1 || x+4 > n || y-2 < 1 || y+3 > m)return 0;
for(int i = 0; i < 12; i++)
int nx = x+dx[i], ny = y+dy[i];
if(a[nx][ny] != '.')return 0;
int res = 0;
for(int i = x-1; i <= x+4; i++)
for(int j = y-2; j <= y+3; j++)
if(a[i][j]=='.')res++;
return res==12;
void solve()
cin>>n>>m;
for(int i = 1; i <= n; i++)cin>>a[i]+1;
//找出所有洞
vector<pair<int,int>>vc;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
if(a[i][j] == '.')
if(check(i,j))
vc.push_back(i,j);
//两两判断哪些是C
int res = 0;
for(int i = 0; i < vc.size(); i++)
for(int j = i+1; j < vc.size(); j++)
int x1 = vc[i].first, y1 = vc[i].second;
int x2 = vc[j].first, y2 = vc[j].second;
if((abs(x1-x2)==7 && y1 == y2) || (abs(y1-y2) == 7 && x1 == x2))res++;
cout<<res<<" "<<((int)vc.size()-2*res)<<"\\n";
int main()
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int T = 1; //cin>>T;
while(T--)
solve();
return 0;
I.Barbecue
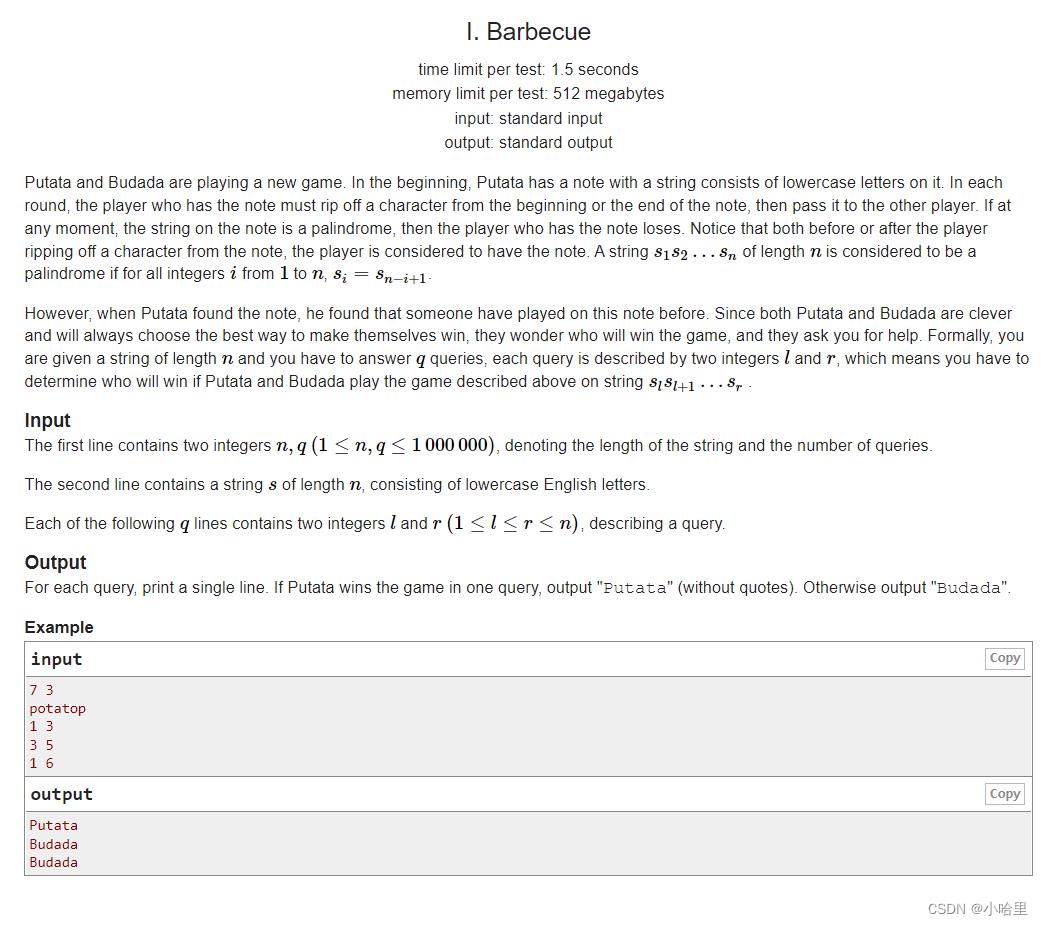
题意:
- 给定一个长度为 n 的字符串 S,q 次询问,每次询问指定 S 的一个子串,两个人在该子串上进行博弈。
- 博弈双方轮流删去当前串开头或结尾的一个字符,碰到回文串的人输。
预测两人都按最优策略操作时最终谁会获胜。 - n, q < 1e6
思路:
- 首先通过 Hash 或马拉车 等方式 O(1) 特判起始串为回文串的情况。
- 对于接下来任意一个局面,先手操作前一定不是回文串。若先手无法进行任何操作,则说明无论删去开头还是结尾都会得到回文串。
- 容易发现满足条件的串只能形如 ab, abab, ababab, . . .这说明终止态的长度一定是偶数,因此输赢只和起始串长度的奇偶性有关。
- 时间复杂度 O(n + q)。
//马拉车
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n,q,l,r;
string s;
int main()
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,q;
string s;
cin>>n>>q>>s;
vector<int> d1(n);
for(int i = 0, l = 0,r = -1; i < n; i++)
int k = (i > r) ? 1 : min(d1[l + r - i],r - i + 1);
while(0 <= i - k && i + k < n && s[i - k] == s[i + k]) k++;
d1[i] = k--;
if(i + k > r)
l = i - k;
r = i + k;
while(q--)
cin>>l>>r;
l--,r--;
int mid = (l + r)/2;
以上是关于ZJCPC2022 第19届 浙江省赛The 19th Zhejiang Provincial Collegiate Programming Contest(CBALGMIF 8题)的主要内容,如果未能解决你的问题,请参考以下文章