三维坐标点到直线的距离公式是啥?

Posted 2023-04-27

三维坐标点到直线的距离公式是：点P(x0,y0,z0)到直线A1x+B1y+C1z+D1=0 A2x+B2y+C2z+D2=0 距离的一个公式:d=|(A1x0+B1y0+C1z0+D1)n→2-(A2x0+B2y0+C2z0+D2)n→1||n→1×n→2|其中n→i=Ai,Bi,Ci,(i=1,2)。

空间点到直线的方程是：(x-x0)/a=(y-y0)/b=(z-z0)/c。

(1)理解点到直线距离公式的推导过程，并且会使用公式求出定点到定直线的距离。

(2)了解两条平行直线的距离公式，并能推导。

证明方法：

1、函数法

证：点P到直线上任意一点的距离的最小值就是点P到直线的距离。在上取任意点用两点的距离公式有，为了利用条件上式变形一下，配凑系数处理得：当且仅当时取等号所以最小值。

2、不等式法

证：点P到直线上任意一点Q的距离的最小值就是点P到直线的距离。由柯西不等式：当且仅当时取等号所以最小值。

参考技术A 点到线的距离公式如下：
设直线L的方程为Ax+By+C=0，点P的坐标为（x0，y0），则点P到直线L的距离为：

定义法证明：
根据定义，点P（x_，y_）到直线l：Ax+By+C=0的距离是点P到直线l的垂线段的长。
设点P到直线的垂线为l\'，垂足为Q，则l\'的斜率为B/A则l\'的解析式为y-y_=（B/A）（x-x_）。
把l和l\'联立得l与l\'的交点Q的坐标为（（B^2x_-ABy_-AC）/（A^2+B^2），（A^2y_-ABx_-BC）/（A^2+B^2））由两点间距离公式得：
PQ^2=[（B^2x_-ABy_-AC）/（A^2+B^2）-x0]^2+[（A^2y_-ABx_-BC）/（A^2+B^2）-y0]^2=[（-A^2x_-ABy_-AC）/（A^2+B^2）]^2

什么是两点之间的距离 什么定义

在平面上，以这两点为端点的线段的长度就是这两点间的距离。

设两个点A、B以及坐标分别为 ：A（x1，y1），B（x2，y2）则A和B两点之间的距离为：

两点间距离公式常用于函数图形内求两点之间距离、求点的坐标的基本公式，是距离公式之一。两点间距离公式叙述了点和点之间距离的关系。

扩展资料：

点到直线的距离：

直线Ax+By+C=0 坐标（Xo，Yo）那么这点到这直线的距离就为：

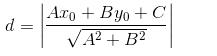
公式描述：

公式中的直线方程为Ax+By+C=0，点P的坐标为(x0,y0)。

连接直线外一点与直线上各点的所有线段中，垂线段最短，这条垂线段的长度，叫做点到直线的距离。

数学中常见的距离：

1、欧氏距离（Euclidean distance），也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离的就是两点之间的距离。

2、曼哈顿距离，出租车几何或曼哈顿距离（Manhattan Distance）是由十九世纪的赫尔曼·闵可夫斯基所创词汇 ，是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。

3、在数学中，切比雪夫距离（Chebyshev distance）或是L∞度量，是向量空间中的一种度量，二个点之间的距离定义是其各坐标数值差绝对值的最大值。以数学的观点来看，切比雪夫距离是由一致范数（uniform norm）（或称为上确界范数）所衍生的度量，也是超凸度量的一种。

参考技术A 一般只考虑平面上的情况：在平面上,一这两点为端点的线段的长度就是这两点间的距离.
对于在球面上,指经过这两点的大弧（在以球心为圆心的圆上）的长度.本回答被提问者和网友采纳 参考技术B 在平面上，以这两点为端点的线段的长度就是这两点间的距离。 参考技术C 答:一般指两个物体之间的直线距离。