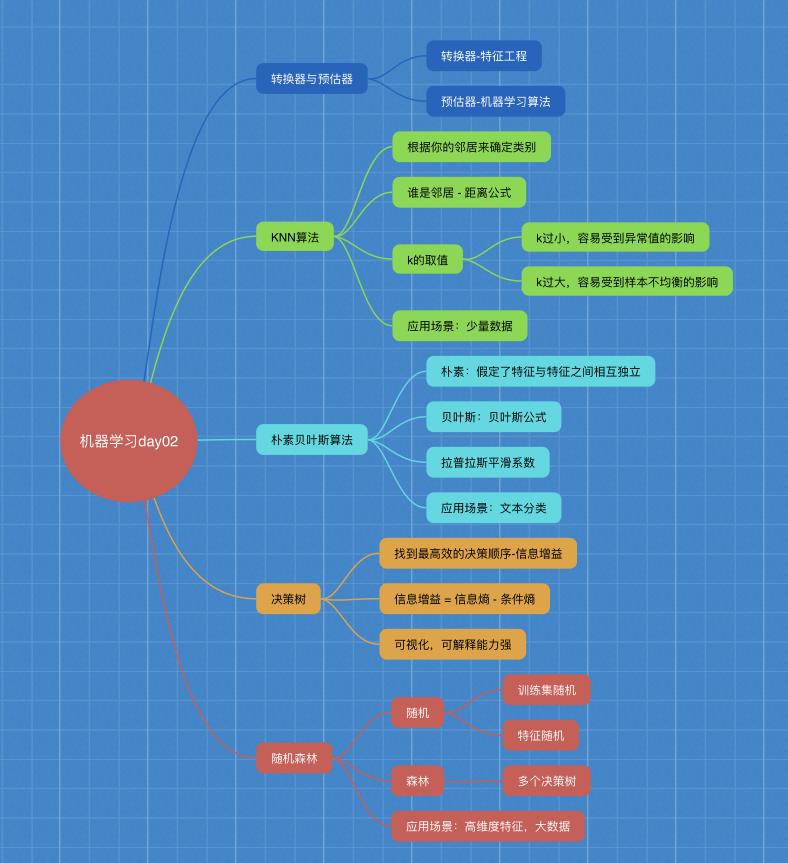
三天爆肝快速入门机器学习：KNN算法朴素贝叶斯算法决策树第二天

Posted 2023-01-17 普通网友

三天爆肝快速入门机器学习【第二天】

• 转换器与预估器
• KNN算法
• 决策树
• 随机森林
• 个人总结

转换器与预估器

必须理解的转换器与估计器

一转化器

回想一下之前做的特征工程的步骤？

实例化（实例化的是一个转换器类transformer)
调用fit_transform(对于文档建立分类词频矩阵，不能同时调用)
我们把特征工程的接口称为转换器，其中转换器调用有如下几种形式.(我们以标准化为例，分析如下三种调用形式的区别.

fit_transform
fit 计算每列的平均值与标准差
transform 进行最终的标准化
from sklearn.preprocessing import StandardScaler
std1=StandardScaler()
a=[[1,2,3],[4,5,6]]
std1.fit_transform(a)
结果如下
array([[-1., -1., -1.], [ 1., 1., 1.]])

print(std1.fit(a))#计算每一列的平均值与标准差
StandardScaler(copy=True, with_mean=True, with_std=True)

std1.transform(a)#进行最终的标准化
array([[-1., -1., -1.],
[ 1., 1., 1.]])

二估计器

1.在sklearn中，估计器是一类实现了算法的API接口

用于分类的估计器
sklearn.neighbors KNN算法
sklearn.naive_bayes 贝叶斯算法
sklearn.linear_model.LogisticRegression逻辑回归
sklearn.tree 决策树与随机森林
用于回归的估计器
sklearn.linear_model.LinearRegression 线性回归
sklearn.linear_model.Ridge
用于无监督学习的估计器
sklearn.cluster.KMeans 聚类算法
2.估计器的工作流程

转化成文字意思就是:利用训练集构建一个机器学习模型，模型构建好之后可以利用测试集来评估我们模型的性能。
3.估计器操作的具体步骤
实例化一个estimator
estimator.fit(x_train,y_train)计算，生产一个机器学习模型
模型评估：
直接比对真实值与预测值

y_predict=estimator.predict(x_test)
y_test==y_predict

计算准确率

accuracy=estimator.score(x_test,y_test)

KNN算法

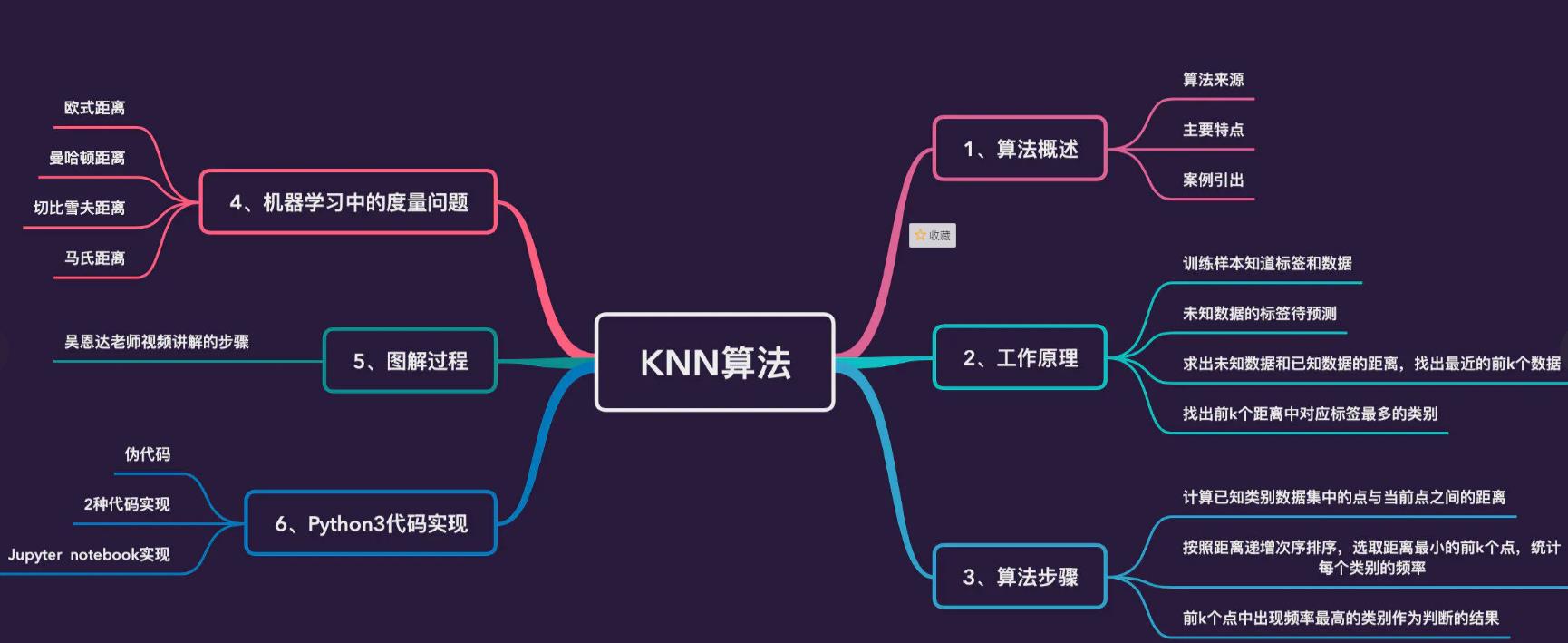
算法概述
k近邻法(k-nearest neighbor, k-NN)是1967年由Cover T和Hart P提出的一种基本分类与回归方法。简单地说，k-近邻算法就是采用不同特征值之间的距离来进行分类，算法主要特点为：

优点：精度高，对异常值不敏感，没有数据输入假定
缺点：计算复杂度高，空间复杂度高
适用数据范围：数值型和标称型（男女）
有人曾经统计过很多电影的打斗镜头和接吻镜头，如下图显示的电影打斗镜头和接吻镜头：

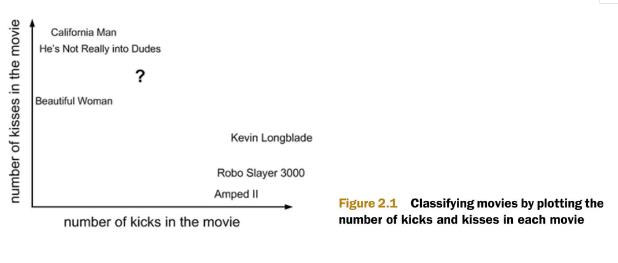
假设有一部未看过的电影，如何确定它是爱情片还是动作片呢？我们看看下表的数据：

当我们不知道未知电影史属于何种类型，我们可以通过计算未知电影和其他电影的距离，按照电影的递增排序，可以找到k个距离最近的电影。在距离最近的电影中，选择类别最多的那部电影，即可判断为未知电影的类型。

比如k=5，这5部电影中3部是爱情片，2部是动作片，那么我们将未知电影归属为爱情片。

工作原理
存在一个样本数据集和数据标签，知道样本和标签的对应关系
输入没有标签的数据，将新数据的每个特征与样本集中数据对应的特征进行比较
提取样本集中特征最相似数据的分类标签，只选取前k个最相似的数据，一般k是小于20
算法步骤
计算已知类别数据集中的点与当前点之间的距离；
按照距离递增次序排序；
选取与当前点距离最小的k个点；
确定前k个点所在类别的出现频率；
返回前k个点所出现频率最高的类别作为当前点的预测分类。

机器学习中向量距离度量准则
下面👇列举了机器学习中常用的向量距离度量准则：

欧式距离
曼哈顿距离
切比雪夫距离
马氏距离
巴氏距离
汉明距离
皮尔逊系数
信息熵

图解过程

Python3版本代码
伪代码
首先给出KNN算法的伪代码（对未知类别属性的数据集中的每个点依次执行以下操作）：

计算已知类别数据集中的点和当前点之间的距离
按照距离递增次序排序
选取与当前距离最小的k个点
确定k个点所在类别的出现频率
返回前k个点出现频率最高的类别作为当前点的预测分类
Python3实现
下面给出实际的Python3代码。使用内置的collections模块来解决：

运行上面的代码，显示的结果为：

dist：待预测的电影和已知电影欧式距离
k_labels：取出排序后前（k=3）3个最小距离的电影对应的类别标签，结果是[“动作片”,“动作片”,“爱情片”]
label：判断的结果是动作片，因为动作片有2票

代码解释
1、函数首先需要生成数据集：关于给出的前4部电影，已知打斗次数和接吻次数，同时还有电影的分类情况；

2、现在新出现了一部电影：打斗次数是98，接吻次数是17，如何确定其属于哪种类型的电影？

打斗次数 接吻次数 电影分类
1 1 101 爱情片
2 5 89 爱情片
3 108 5 动作片
4 115 8 动作片
待预测 98 17 ？
不使用collections模块如何解决？

classfiy函数有4个输入参数：

用于分类的输入向量inX
输入的训练样本集合为dataSet
标签向量为labels
用于选择最近邻居的数目k
其中标签向量的元素数目和矩阵dataSet的行数相同

看看具体的解释：

1、原始数据是什么样子？

打印出来的效果：

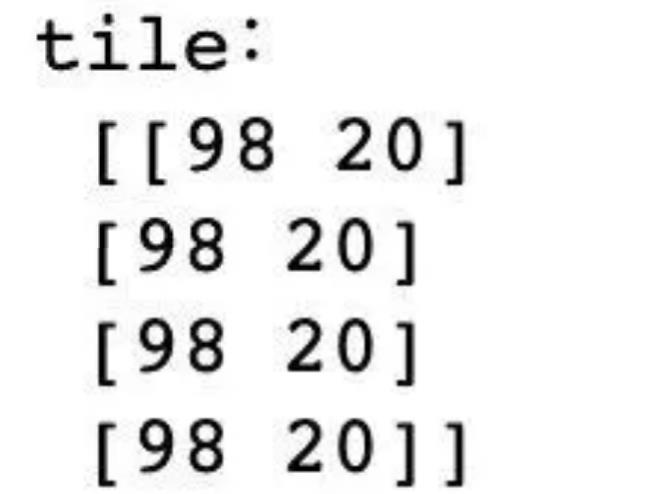
2、为什么使用np.tile方法？

为了和dataSet的shape保持一致，方便后续的求距离

3、每个距离和相对的索引关系

Jupyter notebook中使用KNN算法
步骤
下面也是通过一个模拟的电影数据来讲解如何在jupyter notebook中使用KNN算法，大致步骤分为：

构建数据集
构建一个包含接吻镜头、打斗镜头和电影类型的数据集

2、求距离

求出待预测分类的数据和原数据的欧式距离

3、距离排序

将求出的距离进行升序排列，并取出对应的电影分类

4、指定取出前k个数据

取出指定的前k个数据，统计这些数据中电影类型的频数，找出频数最多的类型，即可判断为未知待预测电影的类型

代码
1、模拟数据：

2、求解距离

3、对距离升序排列

4、取出前k个数并统计频数

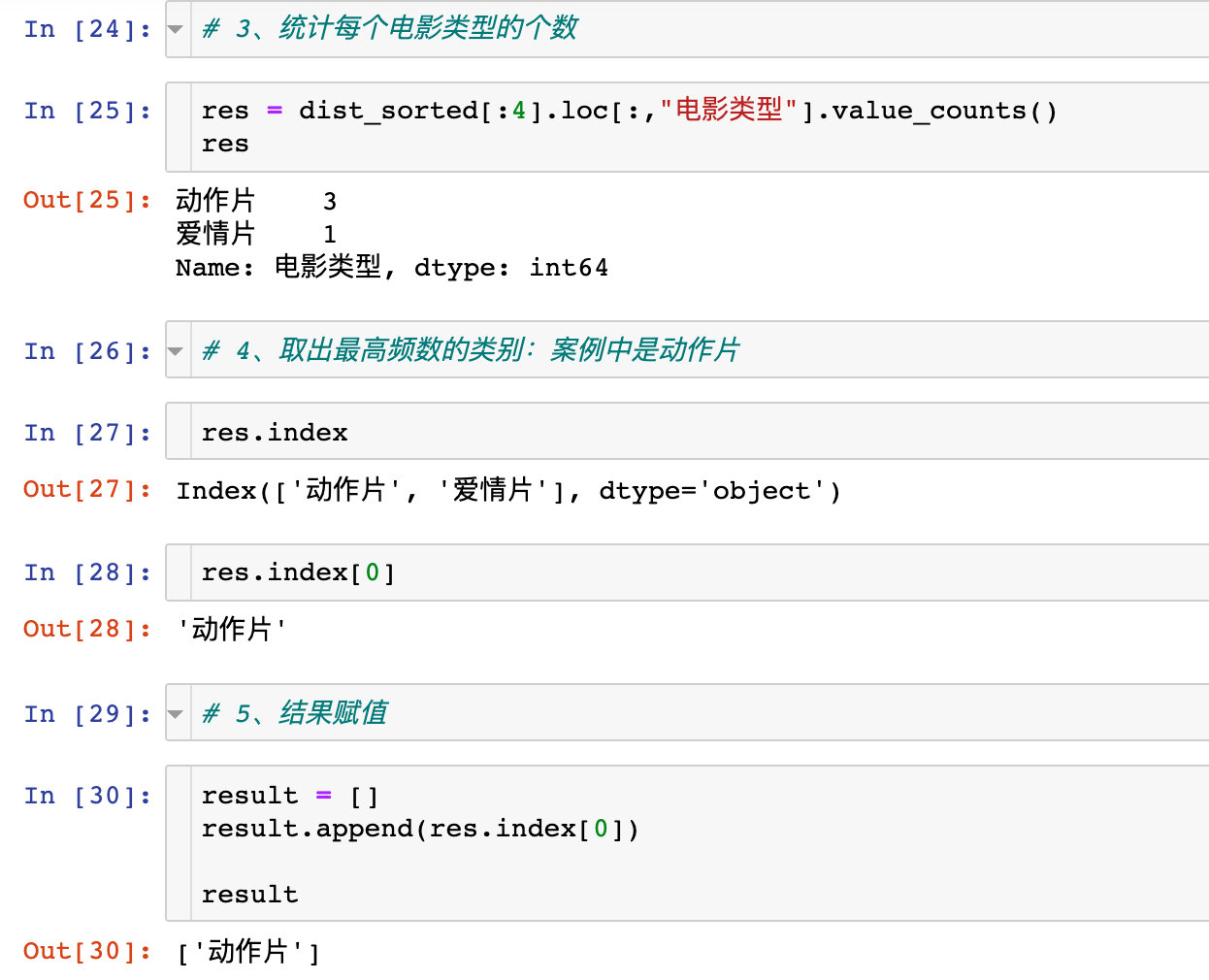
封装成函数
将上面的整个过程封装成函数：

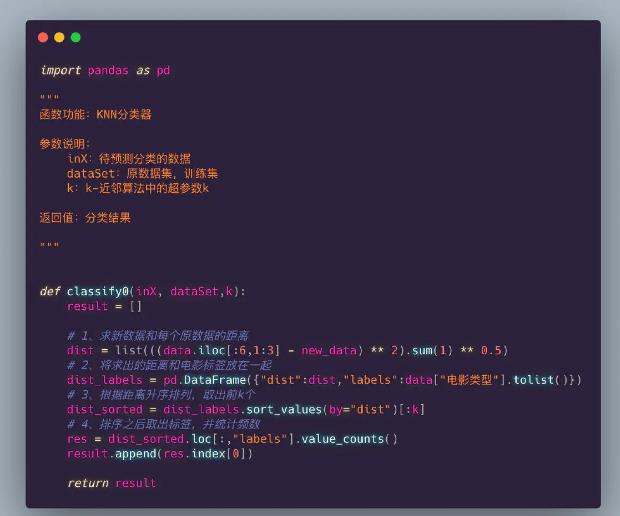
import pandas as pd

"""
函数功能：KNN分类器

参数说明：
    inX：待预测分类的数据
    dataSet：原数据集，训练集
    k：k-近邻算法中的超参数k
    
返回值：分类结果

"""

def classify0(inX, dataSet,k):
    result = []
    
    # 1、求新数据和每个原数据的距离
    dist = list(((data.iloc[:6,1:3] - new_data) ** 2).sum(1) ** 0.5)
    # 2、将求出的距离和电影标签放在一起
    dist_labels = pd.DataFrame("dist":dist,"labels":data["电影类型"].tolist())
    # 3、根据距离升序排列，取出前k个
    dist_sorted = dist_labels.sort_values(by="dist")[:k]
    # 4、排序之后取出标签，并统计频数
    res = dist_sorted.loc[:,"labels"].value_counts()
    result.append(res.index[0])
    
    return result

利用上面模拟的数据测试一下我们封装的代码，结果是相同的

决策树

决策树学习是应用最广泛的归纳推理算法之一。它是一种逼近离散数值目标函数的方法，在这种方法中学习到的函数被表示为一棵决策树。学习得到的决策树也能再被表示为多个if-then的规则，以提高可读性。这种学习算法是最流行的归纳推理算法之一，已经成功的应用到从学习医疗诊断到学习评估贷款申请的信用风险的广阔领域。经典的决策树学习方法包括像ID3（Quinlan 1986年）、ASSISTANT和C4.5（Quinlan 1993年）这样广为应用的算法。

在这里要说一句题外话，随着大数据、人工智能技术的兴起，目前这些领域应用神经网络进行深度学习更为流行。但是想想在1986年就有决策树这样的算法诞生，将人从重复、繁琐的工作中释放出来，而且效果还挺不错的，多么令人兴奋。

决策树的表示
下面我们首先来解决第一个问题，也就是what的问题。我们依旧拿Tom大神在Machine Learning一书中的一段叙述以及例子进行学习。

决策树通过把实例从根结点排列（sort）到某个叶子结点来分类实例，叶子结点即为实例所属的分类。树上的每一个结点指定了对实例的某个属性（attribute）的测试，并且该结点的每一个后继分支对应于该属性的一个可能值。分类实例的方法是从这棵树的根结点开始，测试这个结点指定的属性，然后按照给定实例的该属性值对应的树枝向下移动。这个过程再在以新结点为根的子树上重复。

简而言之，决策树首先是一棵树。没错，就是数据结构中所指的树。树中的非叶子节点都是数据在某一维的属性，叶子节点是数据的输出结果。用简单的形式化的语言表示的话，可以令一个数据样本为X=(x_1,x_2,…,x_n)，该数据样本对应的输出为y。那么决策树中非叶子节点则是x_i，叶子节点则是y。

千言万语不如一张图，我们使用书中的一个例子，例子是根据当前的天气的情况（即X），来分类“星期六上午是否适合打网球”（y）。决策树如下图示例所示。

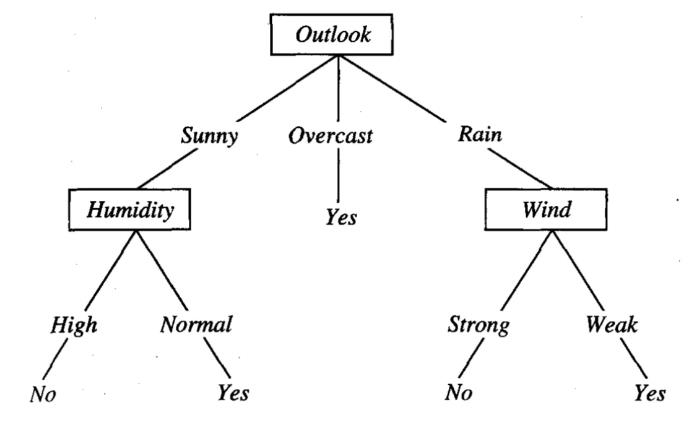
图中的决策树上非叶子节点的Outlook、Humidity、Wind既是上述的x_i，而树干上的值即是属性x_i对应的值，例如Humidity对应的High和Normal。而叶子节点Yes和No既是上述的y。例如，下面的实例：<Outlook=Sunny，Temperature=Hot，Humidity=High，Wind=Strong>将被沿着这棵决策树的最左分支向下排列，因而被评定为反例，即No。

到此我们已经对决策树的概念有了一个基本的了解。

决策树是一棵树。
决策树是用来对离散数据进行分类的。
非叶子节点上是数据的某一项属性，叶子节点是数据的分类结果。

基础的决策树学习算法
在弄清楚what问题后，我们下一步的疑惑便是决策树是怎么生成的，即给了你一组样本数据后，如何从数据中学习出来这一棵神奇的决策树。话不多说，我们开始围绕how这一个主题来继续。

大多数已开发的决策树学习算法是一种核心算法的变体。该算法采用自顶向下的贪婪搜索遍历可能的决策树空间。也就是说决策树的学习问题可以看做是一个搜索问题，是从由数据各个维度的属性张成的空间中，搜索得到一个合适的解的过程。这一核心算法是ID3算法（Quinlan 1986）和后继的C4.5算法（Quinlan 1993）的基础，我们选择这一基本的算法进行讨论学习。

基本的ID3算法通过自顶向下构造决策树来进行学习。那么我们就要问了，该选择哪一个属性作为根节点来进行测试呢？答曰：选择分类能力最好的属性作为根节点。我们又要问了，什么样的属性我们可以说它的分类能力好？这里我们先卖个关子，种个草，回头再来拔草。我们先保持思路继续往前。当我们选择了分类能力最好的属性作为根节点后，那么所有的数据根据该属性可以分成几个分支（分支的个数即属性的取值个数）。在不同分支下的数据，我们又可以按照上面的操作，选择分支下的自数据集里分类能力最好的属性作为“根”节点（即分支里的根节点）。如此迭代，就可以得到一棵决策树。听起来，挺简单的吧。

好了，我们发现算法的核心是如何选取每一个节点要测试的属性，我们希望是选择的属性是有助于分类的，也就是上面所提到的分类能力强。那么啥叫分类能力强呢？这里我们就要定义一个统计数值，称作信息增益（information gain）**，我们用这个属性来衡量属性的分类能力。一看到“信息”这两个字，我们立刻就会联想到熵。没错，就是香农提出的信息熵（你大爷还是你大爷，提出来的东西应用就那么广泛，计算机网络中也有我，机器学习依旧还有我）。关于信息熵更多的知识，大家可以去阅读更多的文章。继续回到主题，信息增益如何定义呢？我们先回顾下信息熵的概念，对于一个随机变量x，令它的概率密度为p(x)，不失一般性的我令x是一个离散变量，那么x的信息熵可表示为H(x)=-\\sum_xp(x)\\log_2p(x)

我们把上述的随机变量替换成一个数据集合，就可以得到一个数据集合的信息熵。举个例子，S是一个相对于某个布尔分类的14个样例的集合，包含9个正例和5个反例。那么S相对于这个布尔分类的信息熵为Entropy(S)=-(9/14)\\log_29/14-5/14\\log_25/14=0.940

已经有了信息熵作为信息的衡量标准，那么我们可以进一步的定义信息增益。

信息增益就是由于使用这个属性分割样本数据集而导致的信息熵的降低。

我们可以这样来理解，使用某个属性分割样本数据集，相当于我们获取了数据中这一个属性的信息。使用这个属性对数据集进行分类，使得我们对于数据集的了解更加清晰，信息熵便会下降。信息熵下降前后的差值既是该属性的信息增益。形式化的表示如下所示，
Gain(S,A)=Entropy(S)-\\sum_v \\in Values(A) \\frac|S_v||S|Entropy(S_v)

其中Values(A)代表属性A的取值集合，S_v是S中属性A取值为v的集合。所以Gain(S,A)是由于给定了属性A的值而导致的信息熵的减少（熵代表的是系统的混沌状态，给定了信息后，系统的熵值减少，意味着状态更加确定）。换句话来讲，Gain(S,A)是由于给定属性A的值而得到的关于目标函数值的信息。当对S的一个任意成员的目标值编码时，Gain(S,A)的值是在知道属性A的值后可以节省的二进制位数。说到这里大家是不是想起一种编码方式？是的，没错，就是哈夫曼编码（Huffman Coding），在这里就不展开讨论了，依旧还是站在香农的肩膀上。

好了，又到了举例子的时候了。为了演示ID3算法的具体操作，考虑使用下表中的训练数据来进行。

这里，目标属性PlayTennis对于不同的星期六上午具有yes和no两个值，我们将根据其他属性来预测这个目标属性值。首先考虑算法的第一步，选择哪一个属性作为根节点。ID3算法将计算每一个候选属性（Outlook、Temperature、Humidity、Wind）的信息增益，然后选择其中最高的一个。我们可以计算得到
Gain(S,Outlook)=0.246
Gain(S,Humidity)=0.151
Gain(S,Wind)=0.048
Gain(S,Temperature)=0.029
所以Outlook被作为根节点的决策属性，并为它的每一个可能值（也就是Sunny，Overcast和Rain）在根结点下创建分支。部分决策树的结果显示在图1中，同时画出的还有被排列到每个新的后继结点的训练样例。注意到每一个Outlook=Overcast的样例也都是PlayTennis的正例。所以，树的这个结点成为一个叶子结点，它对目标属性的分类是PlayTennis=Yes。相反，对应Outlook=Sunny和Outlook=Rain的后继结点还有非0的熵，所以决策树会在这些结点下进一步展开。

对于非终端的后继结点，再重复前面的过程选择一个新的属性来分割训练样例，这一次仅使用与这个结点关联的训练样例。已经被收编入树的较高结点的属性被排除在外，以便任何给定的属性在树的任意路径上最多仅出现一次。对于每一个新的叶子结点继续这个过程，直到满足以下两个条件中的任一个：

所有的属性已经被这条路径包括。
与这个结点关联的所有训练样例都具有同样的目标属性值（也就是它们的熵为0）。
决策树学习的归纳偏置
ID3算法从观测到的训练数据泛化以分类未见实例的策略是什么呢？换句话说，它的归纳偏置是什么？这也是就关于why的问题。

如果给定一个训练样例的集合，那么我们能够找到很多决策树来满足这个训练样例集合，为什么ID3算法从千千万万（也许实际上没那么多）棵树中选择了这一棵呢？ID3选择在使用简单到复杂的爬山算法遍历可能的树空间时遇到的第一个可接受的树。概略地讲，ID3的搜索策略为：

优先选择较短的树而不是较长的树。
选择那些信息增益高的属性离根结点较近的树。
近似的ID3算法归纳偏置：较短的树比较长的优先。那些信息增益高的属性更靠近根结点的树得到优先。

那么为什么优先最短的假设呢？ID3算法中优选较短决策树的归纳偏置，是不是从训练数据中泛化的可靠基础？哲学家们以及其他学者已经对这样的问题争论几个世纪了，而且这个争论至今还未解决。威廉•奥坎姆大约在1320年提出类似的论点 ，是最早讨论这个问题的人之一，所以这个偏置经常被称为“奥坎姆剃刀”（Occam’s razor）。

奥坎姆剃刀：优先选择拟合数据的最简单假设。

这个问题就显得很哲学了。在回归问题里，我们也能找到类似的例子，例如给了一个九个点的样本数据，我们总能找到一个多项式y=\\sum_i=0^8w_ixi，使得这条曲线完美的穿过这9个点，但是这样一条曲线真的能代表这些数据的实际情况么。例如，数据点是关于房子面积和房价的数据（扎心了吧）。显然这样一条曲线的泛化能力是很差的。所以奥坎姆剃刀法则是对“Simple is best”的诠释。

当然给出一个归纳偏置的名字不等于证明了它。为什么应该优先选择较简单的假设呢？请注意科学家们有时似乎也遵循这个归纳偏置。例如物理学家优先选择行星运动简单的解释，而不用复杂的解释。为什么？一种解释是短假设的数量少于长假设（基于简单的参数组合），所以找到一个短的假设但同时它与训练数据拟合的可能性较小。相反，常常有很多非常复杂的假设拟合当前的训练数据，但却无法正确地泛化到后来的数据。例如考虑决策树假设。500个结点的决策树比5个结点的决策树多得多。如果给定一个20个训练样例的集合，可以预期能够找到很多500个结点的决策树与训练数据一致，而如果一个5结点的决策树可以完美地拟合这些数据则是出乎意外的。所以我们会相信5个结点的树不太可能是统计巧合，因而优先选择这个假设，而不选择500个结点的。

关于why问题的讨论就到这里，其实还有很多的解释以及可以探讨的地方，大家可以阅读更多的材料来解开谜题。

代码示例
在这部分，我们将使用scikit-learn（python语言编写的机器学习包）中的决策树算法库来进行演示。实际动手操作总归会带来对算法不一样的感受。上文中我们只是对最基础的决策树算法ID3进行了理论分析和算法描述，而scikit-learn中包含的决策树算法多种多样。但是核心思想大同小异，更详细的算法细节大家可以阅读大神们的论文、python源码或者文档说明进行了解。

代码如下：

from sklearn.datasets import load_iris
from sklearn import tree
import pydotplus

iris = load_iris()
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)
dot_data = tree.export_graphviz(clf, out_file=None,
                                feature_names=iris.feature_names,
                                class_names=iris.target_names,
                                filled=True, rounded=True,
                                special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("iris.pdf")

数据集是鸢尾植物数据库花瓣以及萼片的长和宽共四项数据，输出为鸢尾植物的种类setosa、versicolor和virginica三种（更多的信息在代码里debug下，观察iris变量即可）。最后的分类输出如下图。

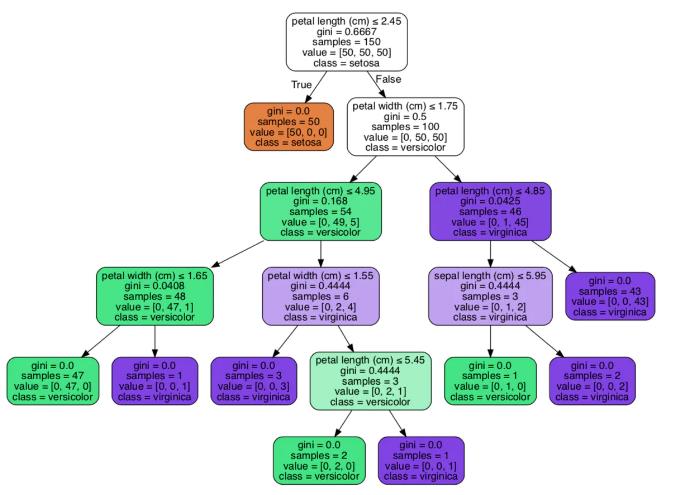
我们得到了一棵通过学习算法学习得到的决策树。这里我们可以看到我们没有使用信息熵当做选择根节点的依据，而是选择了gini值，本着学一练二考三的科研训练方法（大学本科某著名教授所提出的，这样的强度确实酸爽），留给大家自己去探索更多的细节。

随机森林

集成学习
通过构建并结合多个分类器来完成学习任务。将多个学习器进行结合，常比获得单一学习器更好的泛化性能。
目前集成学习方法大致可分为两类，即个体学习器之间存在强依赖关系，必须串行生成的序列化方法，以及个体学习器之间不存在依赖关系，可同时生成的并行化方法；前者代表时Boosting， 后者代表是Bagging和随机森林(random forest: RF)。

Bagging 和随机森林
要得到泛化性能强的集成，则集成中的个体学习器应尽可能相互独立。
“自助采样法”：给定包含m个样本的数据集， 先随机选取一个样本放入采样集中，再把该样本放回，重复m次随机操作，得到含m个样本的采样集。这样使得初始训练集中有的样本在采样集中出现，有的从未出现。
如此，可以采样出T个含m个样本的采样集，基于每个采样集训练出一个基础学习器，将这些基础学习器进行结合，这就是Bagging的基本流程。在对预测输出进行结合时， Bagging通常对分类任务使用简单投票，对回归任务使用简单平均法。

关于决策树：
决策树实际是将空间用超平面(后面介绍svm也会提到)进行划分的一种方法，每次分割，都将当前空间一份为二。

这样使得每一个叶子节点都是在空间中的一个不相交的区域。决策时，会根据输入样本每一维feature的值，一步步往下，最后使样本落入N个区域中的一个(假设有N个叶子节点)。
随机森林是Bagging的一个扩展。随机森林在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入随机属性选择(引入随机特征选择)。传统决策树在选择划分属性时在当前节点的属性结合(d个属性)，利用信息论的知识选取一个最优属性；而在随机森林中， 对决策树的每个节点，先从该节点的属性集合中随机选取包含k个属性的子属性集，然后选择最优属性用于划分。这里的参数k控制了随机性的引入程度。若k=d， 则是一般的决策树；k=1， 则是随机选择一个属性进行划分。随机森林对用做构建树的数据做了限制，使的生成的决策树之间没有关联，提升算法效果。

随机森林的分类
随机森林用于分类是，即采用n个决策树分类，将分类结果用简单投票得到最终分类，提高准确率。
随机森林是对决策树的集成，其两点不同也在上面叙述中提到：

采样差异：从含m个样本的数据集中有放回采样，得到含m个样本的采样集用于训练。保证每个决策树的训练样本不完全一样。
特征选择差异：每个决策树的k个分类特征是所在特征中随机选择的(k需要调参)。
随机森林需要调整的参数：

决策树的个数m
特征属性的个数 k
递归次数(决策树的深度)

实现流程
导入数据并将特征转为float形式。
将数据集分成n份， 方便交叉验证
构造数据子集(随机采样)，并在指定特征个数(假设m个，调参)下选择最优特征
构造决策树(决策树的深度)
创建随机森林(多个决策树的结合)
输入测试集并进行测试，输入预测结果。
随机森林的优点：

在当前的很多数据集上，相对其他算法有着很大的优势
能够处理高纬度(feature)的数据， 并且不同做特征选择。
在训练完后，能够给出哪些feature比较重要
创建随机森林时， 对generlization error使用的是无偏估计
训练速度快
在训练过程中，能够监测到feature间的相互影响
容易做成并行化方法
理解，实现简单
基本理解后，可以参考一下别人和sklearn的相关算法实现，可能的话，我也会做个简单实现。

个人总结

用笔记本码字还是不太习惯，不敢太用力。平时用键盘打字习惯了，前后后花了几个小时才敲完，中间可能会出现一些错误，欢迎大家指出来。这是机器学习的第二篇文章，点赞过一百立马安排最后一篇文章。