课后习题答案 严蔚敏 等 编著

Posted 2023-01-14 来老铁干了这碗代码

所有章节答案合集——>传送门

---

1．选择题
（ 1）把一棵树转换为二叉树后，这棵二叉树的形态是（） 。
A．唯一的
Ｂ．有多种
C．有多种，但根结点都没有左孩子
Ｄ．有多种，但根结点都没有右孩子
答案： A
解释：因为二叉树有左孩子、右孩子之分，故一棵树转换为二叉树后，这棵二叉树的
形态是唯一的。

（ 2）由 3 个结点可以构造出多少种不同的二叉树？（）
A． 2 B ． 3 C ． 4 D ． 5
答案： D

（ 3）一棵完全二叉树上有 1001 个结点，其中叶子结点的个数是（） 。
A． 250 B ． 500 C ． 254 D ． 501
答案： D
解释：设度为 0 结点（叶子结点）个数为 A，度为 1 的结点个数为 B，度为 2 的结点个数为 C，有A=C+1， A+B+C=1001 ，可得 2C+B=1000 ，由完全二叉树的性质可得 B=0 或 1，又因为 C 为整数，所以 B=0， C=500 ， A=501 ，即有 501 个叶子结点。

（ 4）一个具有 1025 个结点的二叉树的高 h 为（）。
A． 11 B ． 10 C ． 11 至 1025 之间 D． 10 至 1024 之间
答案： C
解释：若每层仅有一个结点，则树高 h 为 1025 ；且其最小树高为 log 2 1025 + 1=11 ， 即 h 在 11 至 1025 之间。

（ 5）深度为 h 的满 m叉树的第 k 层有（）个结点。 (1=<k=<h)
A． m^(k-1)
B． m^k-1
C． m^(h-1)
D． m^h-1
答案： A
解释：深度为 h 的满 m 叉树共有 mh
-1 个结点，第 k 层有 m
k-1 个结点。

（ 6）利用二叉链表存储树，则根结点的右指针是（） 。
A．指向最左孩子 B ．指向最右孩子 C ．空 D ．非空
答案： C
解释：利用二叉链表存储树时，右指针指向兄弟结点，因为根节点没有兄弟结点，故根节点的右指针指向空。

（ 7）对二叉树的结点从 1 开始进行连续编号，要求每个结点的编号大于其左、右孩子的编号，同一结点的左右孩子中，其左孩子的编号小于其右孩子的编号，可采用（）遍历实现编号。
A．先序 B. 中序 C. 后序 D. 从根开始按层次遍历
答案： C
解释：根据题意可知按照先左孩子、再右孩子、最后双亲结点的顺序遍历二叉树，即后序遍历二叉树。

（ 8）若二叉树采用二叉链表存储结构，要交换其所有分支结点左、右子树的位置，利用（）遍历方法最合适。
A．前序 B．中序 C．后序 D ．按层次
答案： C
解释：后续遍历和层次遍历均可实现左右子树的交换 ，不过层次遍历的实现消耗比后续大，后序遍历方法最合适。

（ 9）在下列存储形式中， （）不是树的存储形式？
A．双亲表示法 B ．孩子链表表示法 C．孩子兄弟表示法 D．顺序存储表示法
答案： D
解释：树的存储结构有三种：双亲表示法、孩子表示法、孩子兄弟表示法，其中孩子兄弟表示法是常用的表示法，任意一棵树都能通过孩子兄弟表示法转换为二叉树进行存储。

（ 10）一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满
足（）。
A．所有的结点均无左孩子
B ．所有的结点均无右孩子
C．只有一个叶子结点
D ．是任意一棵二叉树
答案： C
解释：因为先序遍历结果是“中左右” ，后序遍历结果是“左右中” ，当没有左子树时，
就是“中右”和“右中” ；当没有右子树时，就是“中左”和“左中” 。则所有的结点均无左
孩子或所有的结点均无右孩子均可，所以 A、B 不能选，又所有的结点均无左孩子与所有的结
点均无右孩子时，均只有一个叶子结点，故选 C。

（ 11）设哈夫曼树中有 199 个结点，则该哈夫曼树中有（）个叶子结点。
A． 99 B． 100
C． 101 D． 102
答案： B
解释：在哈夫曼树中没有度为 1 的结点，只有度为 0（叶子结点）和度为 2 的结点。设叶子结点的个数为 n0，度为 2 的结点的个数为 n2，由二叉树的性质 n0=n2+1 ，则总结点数 n= n0+n2=2*n0-1 ，得到 n0=100 。

（ 12）若 X 是二叉中序线索树中一个有左孩子的结点，且 X 不为根，则 X 的前驱为（） 。
A． X 的双亲
B． X 的右子树中最左的结点
C． X 的左子树中最右结点
D． X 的左子树中最右叶结点
答案： C

（ 13）引入二叉线索树的目的是（） 。
A．加快查找结点的前驱或后继的速度
B．为了能在二叉树中方便的进行插入与删除
C．为了能方便的找到双亲
D．使二叉树的遍历结果唯一
答案： A

（ 14）设 F 是一个森林， B 是由 F 变换得的二叉树。若 F 中有 n 个非终端结点，则 B 中右指针域为空的结点有（ ）个。
A． n- 1 B． n C． n + 1 D． n + 2
答案： C

（ 15）n（ n≥2）个权值均不相同的字符构成哈夫曼树， 关于该树的叙述中， 错误的是 （ ）。
A．该树一定是一棵完全二叉树
B．树中一定没有度为 1 的结点
C．树中两个权值最小的结点一定是兄弟结点
D．树中任一非叶结点的权值一定不小于下一层任一结点的权值
答案： A
解释：哈夫曼树的构造过程是每次都选取权值最小的树作为左右子树构造一棵新的二叉
树，所以树中一定没有度为 1 的结点、两个权值最小的结点一定是兄弟结点、任一非叶结点
的权值一定不小于下一层任一结点的权值。

---

2．应用题

（1）试找出满足下列条件的二叉树
① 先序序列与后序序列相同②中序序列与后序序列相同
③ 先序序列与中序序列相同④中序序列与层次遍历序列相同
答案：先序遍历二叉树的顺序是“根—左子树—右子树” ，中序遍历“左子树—根—右
子树”，后序遍历顺序是： “左子树—右子树―根＂，根据以上原则有
①或为空树，或为只有根结点的二叉树
② 或为空树，或为任一结点至多只有左子树的二叉树．
③ 或为空树，或为任一结点至多只有右子树的二叉树．
④或为空树，或为任一结点至多只有右子树的二叉树

---

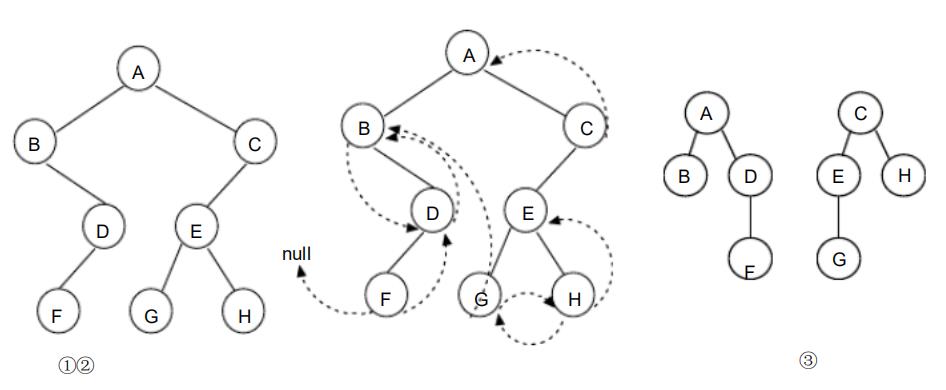
（2）设一棵二叉树的先序序列： A B D F C E G H ，中序序列： B F D A G E H C
①画出这棵二叉树。
②画出这棵二叉树的后序线索树。
③将这棵二叉树转换成对应的树（或森林） 。
答案

---

（ 3）假设用于通信的电文仅由 8 个字母组成， 字母在电文中出现的频率分别为 0.07 ，0.19 ，
0.02 ， 0.06 ， 0.32 ， 0.03 ， 0.21 ， 0.10 。
①试为这 8 个字母设计赫夫曼编码。
② 试设计另一种由二进制表示的等长编码方案。
③对于上述实例，比较两种方案的优缺点。
答案：方案 1；哈夫曼编码
先将概率放大 100 倍，以方便构造哈夫曼树。
w=7,19,2,6,32,3,21,10 ，按哈夫曼规则： 【 [ (2,3)， 6], (7,10) 】 … 19,21,32

方案 1 的 WPL ＝ 2(0.19+0.32+0.21)+4(0.07+0.06+0.10)+5(0.02+0.03)=1.44+0.92+0.25=2.61
方案 2 的 WPL ＝ 3(0.19+0.32+0.21+0.07+0.06+0.10+0.02+0.03)=3
结论：哈夫曼编码优于等长二进制编码

---

（ 4）已知下列字符 A、 B、 C、D、E、 F、 G的权值分别为 3、 12 、7、4、 2、 8， 11，试
填写出其对应哈夫曼树 HT 的存储结构的初态和终态。
答案：

---

3．算法设计题
以二叉链表作为二叉树的存储结构，编写以下算法：
（ 1）统计二叉树的叶结点个数。
[ 题目分析 ] 如果二叉树为空，返回 0，如果二叉树不为空且左右子树为空，返回 1，如果
二叉树不为空，且左右子树不同时为空，返回左子树中叶子节点个数加上右子树中叶子
节点个数。
[ 算法描述 ]

int LeafNodeCount(BiTree T) 
 
	if(T==NULL) 
		return 0; // 如果是空树，则叶子结点个数为 0 
	else if(T->lchild==NULL&&T->rchild==NULL) 
		return 1; // 判断结点是否是叶子结点（左孩子右孩子都为空） ，若是则返回 1 
	else 
		return LeafNodeCount(T->lchild)+LeafNodeCount(T->rchild); 
 

（ 2）判别两棵树是否相等
[ 算法描述 ]

int compareTree(TreeNode* tree1, TreeNode* tree2) 
//用分治的方法做，比较当前根，然后比较左子树和右子树

	bool tree1IsNull = (tree1==NULL); 
	bool tree2IsNull = (tree2==NULL); 
	if(tree1IsNull != tree2IsNull) 
	 
		return 1; 
	 
	if(tree1IsNull && tree2IsNull) 
	// 如果两个都是 NULL ，则相等
		return 0; 
	// 如果根节点不相等，直接返回不相等，否则的话，看看他们孩子相等不相等
	if(tree1->c != tree2->c) 
	 
		return 1; 
	 
	return (compareTree(tree1->left,tree2->left)&compareTree(tree1->right,tree2->right)) 
	(compareTree(tree1->left,tree2->right)&compareTree(tree1->right,tree2->left)); 
// 算法结束

---

（ 3）交换二叉树每个结点的左孩子和右孩子。
[ 题目分析 ] 如果某结点左右子树为空，返回，否则交换该结点左右孩子，然后递归交换
左右子树。
[ 算法描述 ]

void ChangeLR(BiTree &T) 
 
	BiTree temp; 
	if(T->lchild==NULL&&T->rchild==NULL) 
		return; 
	else 
	 
		temp = T->lchild; 
		T->lchild = T->rchild; 
		T->rchild = temp; 
	// 交换左右孩子
	ChangeLR(T->lchild); //递归交换左子树
	ChangeLR(T->rchild); //递归交换右子树
 

---

（ 4）设计二叉树的双序遍历算法（双序遍历是指对于二叉树的每一个结点来说，先访问
这个结点，再按双序遍历它的左子树，然后再一次访问这个结点，接下来按双序遍历它的右
子树）。[ 题目分析 ] 若树为空，返回；若某结点为叶子结点，则仅输出该结点；否则先输出该结
点，递归遍历其左子树，再输出该结点，递归遍历其右子树。
[ 算法描述 ]

void DoubleTraverse(BiTree T) 
 
	if(T == NULL) 
		return; 
	else if(T->lchild==NULL&&T->rchild==NULL) 
		cout<<T->data; // 叶子结点输出
	else 
	 
		cout<<T->data; 
		DoubleTraverse(T->lchild); // 递归遍历左子树
		cout<<T->data; 
		DoubleTraverse(T->rchild); // 递归遍历右子树
	 
 

---

（ 5）计算二叉树最大的宽度 （二叉树的最大宽度是指二叉树所有层中结点个数的最大值） 。 [ 题目分析 ] 求二叉树高度的算法见上题。 求最大宽度可采用层次遍历的方法， 记下各层
结点数，每层遍历完毕，若结点数大于原先最大宽度，则修改最大宽度。
[ 算法描述 ]

int Width(BiTree bt)// 求二叉树 bt 的最大宽度

	if (bt==null) return (0); // 空二叉树宽度为 0 
	else 
	
		BiTree Q[];//Q 是队列，元素为二叉树结点指针，容量足够大
		front=1;rear=1;last=1; 
		//front 队头指针 ,rear 队尾指针 ,last 同层最右结点在队列中的位置
		temp=0; maxw=0; //temp 记局部宽度 , maxw 记最大宽度
		Q[rear]=bt; // 根结点入队列
		while(front<=last) 
		
			p=Q[front++]; temp++; // 同层元素数加 1 
			if (p->lchild!=null) Q[++rear]=p->lchild; // 左子女入队
			if (p->rchild!=null) Q[++rear]=p->rchild; // 右子女入队	
			if (front>last) // 一层结束，
			
				last=rear; 
				if(temp>maxw) maxw=temp; 
				//last 指向下层最右元素 , 更新当前最大宽度
				temp=0; 
			//if 
		//while 
		return (maxw); 
	
// 结束 width 

（ 6）用按层次顺序遍历二叉树的方法，统计树中具有度为 1 的结点数目。
[题目分析 ]
若某个结点左子树空右子树非空或者右子树空左子树非空，则该结点为度为 1 的结点
[算法描述 ]

int Level(BiTree bt) // 层次遍历二叉树，并统计度为 1 的结点的个数

	int num=0; //num 统计度为 1 的结点的个数
	if(bt)
	
		QueueInit(Q); QueueIn(Q,bt);//Q 是以二叉树结点指针为元素的队列
		while(!QueueEmpty(Q)) 
		
			p=QueueOut(Q); cout<<p->data; // 出队 , 访问结点
			if(p->lchild && !p->rchild ||!p->lchild && p->rchild)	num++; 
			// 度为 1 的结点
			if(p->lchild) QueueIn(Q,p->lchild); // 非空左子女入队
			if(p->rchild) QueueIn(Q,p->rchild); // 非空右子女入队
		 //while(!QueueEmpty(Q)) 
	//if(bt) 
	return(num); 
// 返回度为 1 的结点的个数

（ 7）求任意二叉树中第一条最长的路径长度，并输出此路径上各结点的值。
[ 题目分析 ] 因为后序遍历栈中保留当前结点的祖先的信息，用一变量保存栈的最高栈顶
指针，每当退栈时，栈顶指针高于保存最高栈顶指针的值时，则将该栈倒入辅助栈中，辅助
栈始终保存最长路径长度上的结点，直至后序遍历完毕，则辅助栈中内容即为所求。
[ 算法描述 ]

void LongestPath(BiTree bt)// 求二叉树中的第一条最长路径长度

	BiTree p=bt,l[],s[]; 
	//l, s 是栈，元素是二叉树结点指针， l 中保留当前最长路径中的结点
	int i ， top=0,tag[],longest=0; 
	while(p || top>0) 
	
		while(p) 
			s[++top]=p;
			tag[top]=0; 
			p=p->Lc;
		 // 沿左分枝向下
		if(tag[top]==1) // 当前结点的右分枝已遍历
		
			if(!s[top]->Lc && !s[top]->Rc) // 只有到叶子结点时，才查看路径长度
				if(top>longest) 
				
					for(i=1;i<=top;i++) l[i]=s[i]; longest=top; top--;
				 
			// 保留当前最长路径到 l 栈，记住最高栈顶指针，退栈
		 
		else if(top>0) tag[top]=1; p=s[top].Rc; // 沿右子分枝向下
	//while(p!=null||top>0) 
// 结束 LongestPath 

（ 8）输出二叉树中从每个叶子结点到根结点的路径。
[ 题目分析 ] 采用先序遍历的递归方法， 当找到叶子结点 *b 时，由于 *b 叶子结点尚未添加
到 path 中，因此在输出路径时还需输出 b->data 值。
[ 算法描述 ]

void AllPath(BTNode *b,ElemType path[],int pathlen) 

	int i; 
	if (b!=NULL) 
	
		if (b->lchild==NULL && b->rchild==NULL) //*b 为叶子结点
		
			cout << " " << b->data << " 到根结点路径 :" << b->data; 
			for (i=pathlen-1;i>=0;i--) 
				cout << endl; 
		 
		else 
		
			path[pathlen]=b->data; // 将当前结点放入路径中
			pathlen++; //路径长度增 1 
			AllPath(b->lchild,path,pathlen); // 递归扫描左子树
			AllPath(b->rchild,path,pathlen); // 递归扫描右子树
			pathlen--; //恢复环境
		 
	//if (b!=NULL) 
// 算法结束

---

如果这篇博客对你产生了帮助，还请给给它点个赞哦~，让更多的人看到它。