容积卡尔曼滤波CKF—目标跟踪中的应用(算法部分—I)
Posted 脑壳二
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了容积卡尔曼滤波CKF—目标跟踪中的应用(算法部分—I)相关的知识，希望对你有一定的参考价值。
容积卡尔曼滤波CKF—目标跟踪中的应用(算法部分)
原创不易，路过的各位大佬请点个赞
机动目标跟踪/非线性滤波/传感器融合/导航等探讨代码联系WX: ZB823618313
作者:823618313@qq.com
备注：
容积卡尔曼滤波算法；CKF；Cubature Kalman Filter
两种CKF算法：加性噪声CKF和非加性噪声CKF
本博客主要讲解“加性噪声条件下的容积卡尔曼滤波算法”推导结果
matlab实现;
目标跟踪仿真
Case: 二维目标跟踪情况和三维目标跟踪情况
代码下载地址如下（分别为二维情形和三维情形）
容积卡尔曼滤波2D
https://download.csdn.net/download/weixin_44044161/85401361
容积卡尔曼滤波2D——CT模型
https://download.csdn.net/download/weixin_44044161/85401924
容积卡尔曼滤波2D——RMSE
https://download.csdn.net/download/weixin_44044161/85124145
容积卡尔曼滤波3D——RMSE
https://download.csdn.net/download/weixin_44044161/85124127
无迹卡尔曼滤波UKF—目标跟踪中的应用
容积卡尔曼滤波思考：
为了克服无迹卡尔曼滤波在高维情况下出现滤波精度低的问题，Arasaratnam 和Haykin基于Caubature求积分变换，提出了容积卡尔曼滤波CKF方法。后来众多学者又基于CKF，提出了很多改进版本，如平方根CKF。
对于高斯分布下的非线性滤波问题，实际上就求后验期望的积分。由于被积分函数表现为非线性后验分布与高斯概率密度的乘积，因此一般很难得到解析解。这也是线性系统下该积分可以得到解析解，即著名的卡尔曼滤波算法。
E
[
x
∣
z
]
=
∫
R
f
(
x
)
exp
(
−
x
T
x
)
d
x
E[x|z]=\\int_Rf(x)\\exp(-x^Tx)dx
E[x∣z]=∫Rf(x)exp(−xTx)dx
因此针对该非线性函数的积分问题，营运产生了众多基于数值积分的滤波算法。如UKF通过确定性采样来传播分布的一二阶矩（均值和方差）。而CKF作为看另一种求积分近似方法，利用球面径向规则。
CKF和UKF 总结：
当取
κ
=
0
\\kappa=0
κ=0时， CKF 和 UKF 的估计精度相同，但鉴于 CKF 采样点少，实时性
比 UKF 好，故应选用 CKF 滤波算法；
当
n
≤
2
n\\leq2
n≤2时即低维非线性系统， UKF 的估计精度高于 CKF，应选用 UKF 滤波
算法；
当
n
=
2
n=2
n=2时的非线性系统， UKF 及 CKF 的估计精度相同，但 CKF 的实时性更
好，应选用 CKF 滤波算法；
当
n
≥
3
n\\geq3
n≥3时即高维非线性系统， CKF 的估计精度高于 UKF，应选用 CKF 滤波算法。
下面介绍加性噪声下的容积卡尔曼滤波算法
1、带加性噪声的容积卡尔曼滤波算法CKF
1.1 问题描述（离散时间非线性系统描述）
考虑带加性噪声的一般非线性系统模型，
x
k
=
f
(
x
k
−
1
)
+
w
k
−
1
z
k
=
h
(
x
k
)
+
v
k
(1)
x_k=f(x_k-1) +w_k-1 \\\\ z_k=h(x_k)+v_k \\tag1
xk=f(xk−1)+wk−1zk=h(xk)+vk(1)
其中
x
k
x_k
xk为
k
k
k时刻的目标状态向量。
z
k
z_k
zk为
k
k
k时刻量测向量（传感器数据）。这里不考虑控制器
u
k
u_k
uk。
w
k
w_k
wk和
v
k
v_k
vk分别是过程噪声序列和量测噪声序列，并假设
w
k
w_k
wk和
v
k
v_k
vk为零均值高斯白噪声，其方差分别为
Q
k
Q_k
Qk和
R
k
R_k
Rk的高斯白噪声，即
w
k
∼
(
0
,
Q
k
)
w_k\\sim(0,Q_k)
wk∼(0,Qk),
v
k
∼
(
0
,
R
k
)
v_k\\sim(0,R_k)
vk∼(0,Rk)，且满足如下关系(线性高斯假设)为：
E
[
w
i
v
j
′
]
=
0
E
[
w
i
w
j
′
]
=
0
i
≠
j
E
[
v
i
v
j
′
]
=
0
i
≠
j
\\beginaligned E[w_iv_j'] &=0\\\\ E[w_iw_j'] &=0\\quad i\\neq j \\\\ E[v_iv_j'] &=0\\quad i\\neq j \\endaligned
E[wivj′]E[wiwj′]E[vivj′]=0=0i=j=0i=j
1.2 容积点集
ξ
i
,
w
i
\\\\xi_i, w_i\\
ξi,wi
利用三阶球面径向规则计算标准高斯加权积分，即
E
[
x
∣
z
]
=
∫
R
f
(
x
)
N
(
x
;
0
,
I
)
d
x
≈
∑
i
=
1
m
w
i
f
(
ξ
i
)
E[x|z]=\\int_Rf(x)\\mathcalN(x; 0,I)dx\\approx\\sum_i=1^mw_if(\\xi_i)
E[x∣z]=∫Rf(x)N(x;0,I)dx≈i=1∑mwif(ξi)
式中
ξ
i
=
m
2
[
1
]
i
,
i
=
1
,
2
,
⋯
,
m
=
2
n
w
i
=
1
m
,
i
=
1
,
2
,
⋯
,
m
=
2
n
(2)
\\beginaligned \\xi_i&=\\sqrt\\fracm2[\\mathbf1]_i, i=1,2,\\cdots,m=2n\\\\ w_i&=\\frac1m, i=1,2,\\cdots,m=2n \\endaligned \\tag2
ξiwi=2m[1]i,i=1,2,⋯,m=2n=m1,i=1,2,⋯,m=2n(2)
[
1
]
[\\mathbf1]
[1] 表示
n
n
n（
n
n
n维状态维数） 维空间的点集，即
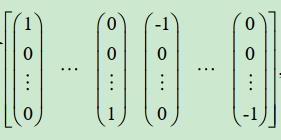
1.3 加性噪声容积卡尔曼滤波CKF算法
1.） 初始化
步骤一：
给定
k
−
1
k-1
k−1以上是关于容积卡尔曼滤波CKF—目标跟踪中的应用(算法部分—I)的主要内容，如果未能解决你的问题，请参考以下文章
交互式多模型-扩展卡尔曼滤波IMM-EKF——机动目标跟踪中的应用
交互式多模型-扩展卡尔曼滤波IMM-EKF——机动目标跟踪中的应用
交互式多模型-无迹卡尔曼滤波IMM-UKF仿真一——机动目标跟踪中的应用