A7.2022年全国数学建模竞赛A题-波浪能最大输出功率设计-赛题分析与讨论

Posted 2023-01-13 YouCans

2022年数学建模国赛（A题/B题/C题）评阅要点

文章目录

• • 1. 2022年A题（波浪能最大输出功率设计）
  • 2. 算法讨论
  • • 2.1 基本分析：阻尼问题，考虑用微分方程求解。
    • 2.2 基本问题：常微分方程还是偏微分方程
    • • 2.3 基本问题：一维问题还是二维问题
      • 2.4 基本问题：一阶问题还是二阶问题
      • 2.5 基本问题：无源问题还是有源问题
      • 2.6 能不能不用微分方程求解？
  • 3. 微分方程例程 — 与题目无关
  • • 3.1 例题：求二阶 RLC 振荡电路的数值解
    • 3.2 二阶微分方程问题的编程步骤
    • 3.3 二阶微分方程问题 Python 例程
    • 3.4 二阶方程问题 Python 例程运行结果
  • 4. 参考文献

1. 2022年A题（波浪能最大输出功率设计）

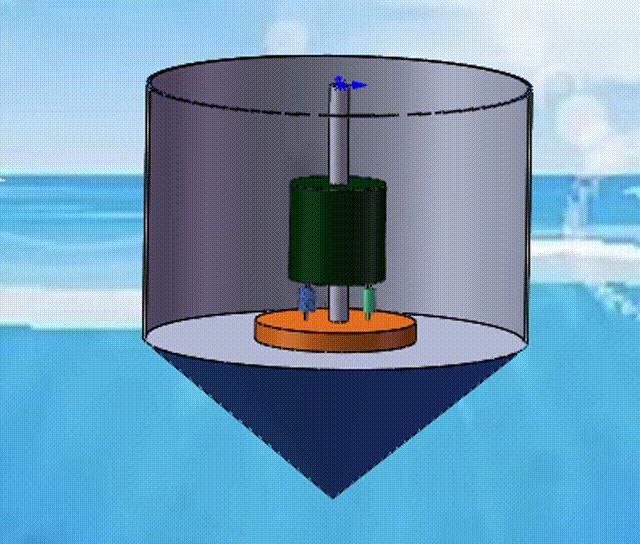
A题 波浪能最大输出功率设计

随着经济和社会的发展，人类面临能源需求环境污染双重挑战，发展可再生产业已成为世界各国的共识。
波浪能作一种重要海洋可再生源，分布广泛储量丰富，具有可观的应用前景。 波浪能装置量转换效率是规模化利关键问题之一。

---

2. 算法讨论

2.1 基本分析：阻尼问题，考虑用微分方程求解。

参考例程：
Python小白的数学建模课-09.微分方程模型09.微分方程模型
Python小白的数学建模课-11.偏微分方程数值解法11.偏微分方程数值解法

2.2 基本问题：常微分方程还是偏微分方程

（1）常微分方程初值问题，可以表达为对 t 或对 x 的导数；
（2）常微分方程边值问题，可以表达为 y 对 x 的导数；
（3）偏微分方程，一般是既包括对 t 的导数，又包括对 x 的导数，当然还有其它特殊形式，就不讨论了。
（4）对于偏微分方程，可以在 t0 或 x0 作为常微分方程讨论，分析和求解。
问题如果涉及 10s, 20s, t 显然是自变量了。
问题如果求某一时刻位移，这当然就是 y(t) 了。
问题如果求某一时刻的速度，可以表示为 y(t) 的一阶导数。

2.3 基本问题：一维问题还是二维问题

（1）中轴，圆柱体，往复运动，垂荡运动，这些都是提示，而且都是必要的。
（2）纵摇，这意味着什么？注意坐标系的选择。推荐参考：
Python小白的数学建模课-11.偏微分方程数值解法11.偏微分方程数值解法

2.4 基本问题：一阶问题还是二阶问题

（1）弹簧-阻尼系统的微分方程，不论串联，并联，串并联，都比较容易列出微分方程。详见“弹簧质量阻尼器的动力学”。
（2）壳体如何处理？取决于坐标系的选择。

2.5 基本问题：无源问题还是有源问题

这个问题很明显，激励力和激励频率都给出了。
有源激励的微分方程，激励函数如何表达与编程，可以参考：
Python小白的数学建模课-09.微分方程模型09.微分方程模型

2.6 能不能不用微分方程求解？

其实是可以的，但难度可能更大，就不讨论了。

---

3. 微分方程例程 — 与题目无关

3.1 例题：求二阶 RLC 振荡电路的数值解

高阶常微分方程，必须做变量替换，化为一阶微分方程组，再用 odeint 求数值解。

零输入响应的 RLC 振荡电路可以由如下的二阶微分方程描述：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{d^{2}u}{d{t}^2}+\frac{R}{L}\ast \frac{du}{dt}+\frac{1}{LC}\ast u=0\\ & u(0)=U_0\\ & u^{\prime }(0)=0\end{array}\end{array}$$

令 $\alpha =R/2L$、${\omega }_0^2=1/LC$，在零输入响应 $u_s=0$ 时上式可以写成：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{d^{2}u}{d{t}^2}+2\alpha \frac{du}{dt}+{\omega }_0^{2}u=0\\ & u(0)=U_0\\ & u^{\prime }(0)=0\end{array}\end{array}$$
对二阶微分方程问题，引入变量 $v=du/dt$，通过变量替换就把原方程化为如下的微分方程组：

$$\{\begin{array}{l}\begin{array}{rl}& \frac{du}{dt}=v\\ & \frac{dv}{dt}=-2\alpha v-{\omega }_0^{2}u\\ & u(0)=U_0\\ & v(0)=0\end{array}\end{array}$$

这样就可以用上节求解微分方程组的方法来求解高阶微分方程问题。

3.2 二阶微分方程问题的编程步骤

以RLC 振荡电路为例讲解 scipy.integrate.odeint() 求解高阶常微分方程初值问题的步骤：

1. 导入 scipy、numpy、matplotlib 包；

2. 定义导数函数 deriv(Y, t, a, w)

   注意 odeint() 函数中定义导数函数的标准形式是 $f(y,t)$ ，本问题中 y 表示向量，记为 $Y=[u,v]$

   导数定义函数 deriv(Y, t, a, w) 编程如下，其中 a, w 分别表示方程中的参数 $\alpha 、\omega$：

# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2*a*v-w*w*u]
    return dY_dt

3. 定义初值 $Y_0=[u_0,v_0]$ 和 $Y$ 的定义区间 $[t_0,t]$；

4. 调用 odeint() 求 $Y=[u,v]$ 在定义区间 $[t_0,t]$ 的数值解。

   例程中通过 args=paras 将参数 (a,w) 传递给导数函数 deriv(Y, t, a, w) 。本例要考察不同参数对结果的影响，这种参数传递方法使用非常方便。

3.3 二阶微分方程问题 Python 例程

# 3. 求解二阶微分方程初值问题(scipy.integrate.odeint)
# Second ODE by scipy.integrate.odeint
from scipy.integrate import odeint  # 导入 scipy.integrate 模块
import numpy as np
import matplotlib.pyplot as plt

# 导数函数，求 Y=[u,v] 点的导数 dY/dt
def deriv(Y, t, a, w):
    u, v = Y  # Y=[u,v]
    dY_dt = [v, -2*a*v-w*w*u]
    return dY_dt

t = np.arange(0, 20, 0.01)  # 创建时间点 (start,stop,step)
# 设置导数函数中的参数 (a, w)
paras1 = (1, 0.6)  # 过阻尼：a^2 - w^2 > 0
paras2 = (1, 1)  # 临界阻尼：a^2 - w^2 = 0
paras3 = (0.3, 1)  # 欠阻尼：a^2 - w^2 < 0

# 调用ode对进行求解, 用两个不同的初始值 W1、W2 分别求解
Y0 = (1.0以上是关于A7.2022年全国数学建模竞赛A题-波浪能最大输出功率设计-赛题分析与讨论的主要内容，如果未能解决你的问题，请参考以下文章
 
 2022年全国大学生数学建模竞赛A题思路
 2022年全国大学生数学建模竞赛A题思路
 2018年数学建模 国赛时间
 Python小白的数学建模课-A4.2021年全国数学建模竞赛 A题分析
 2021全国研究生数学建模竞赛A题思路
 2022年全国大学生数学建模竞赛D题思路