用遗传算法求解配送路线优化问题时，交叉率和变异率怎么设定？

Posted 2023-04-25

如果可以的话，能把遗传算法在这个问题上的思路解释一下吗？论文真心看不懂啊……

以下是问题的详细回答，文字有些长，请你耐心看希望对你有帮助。
传算法可以很好的解决物流配送路径优化问题。但是由于遗传算法交配算子操作可能会使最好解遗失，所以将遗传算法和模拟退火算法结合来解决这一问题。实验结果表明：用这种有记忆功能的遗传模拟退火算法求解物流配送路径优化问题，可以在一定程度上解决上述问题，从而得到较高质量的解。
一 物流系统简介
物流系统是以客户满意为目标，根据顾客的要求条件，从生产地到销售地，在仓储、包装、配送、运输、装卸等环节有机整合所形成的实物、服务以及信息的流通过程所组成的一个复杂的系统。
物流配送是现代化物流管理中的一个重要环节。它是指按用户的定货要求，在配送中心进行分货、配货，并将配好的货物及时送交收货人的活动。本文讨论物流配送中的路径优化问题，并且通过结合模拟退火算法来解决遗传算法在解决此类问题时的不足。
二 系统模型设计
物流配送路径优化问题可以按这样的情况进行描述：从某物流配送中心用多辆配送车辆向多个客户送货。每个客户的位置和货物需求量一定，每辆车的载重量一定，配送时间一定，其一次配送的最大行驶距离一定。要求合理安排车辆配送路线，使目标函数得到最优。并满足以下条件：（1）每条配送路径上各客户需求量之和不超过配送车辆的载重量；（2）每条配送路径的长度不超过配送车辆一次配送的最大行驶距离；（3）每次配送的货物不能超过客 户要求的时间； （4）每个客户的需求必须满足，且只能由一辆配送车送货。设配送中心需要向k个客户送货，每个客户的货物需求量是g （i＝1，2，…..k），每辆配送车的载重量是q，且g 下面建立此问题的数学模型：c 表示点i到点j的运输成本，t 表示从i到s所允许的最大时间。配送中心编号为0，各客户编号为i（i＝1，2，….，k），定义变量如下：
x = 1 或 0（其中，当x 等于1时表示车s由i驶向j；0表示没有该路径。）。
y = 1 或 0（其中，当y 等于1时表示点i的货运任务由s车完成；0表示没有。）。
根据上述变量定义可得到的数学模型如下所示：
min Z ＝ ； （1） ；（2）
＝ 1或 m（其中，当 i = 1，2，……，k时为1，否则为0。）；（3）
＝ y ，j = 1，2，……，k；s = 1，2，……，m； （4）
＝ y ，i = 0，1，……，k；s = 1，2，……，m； （5）
t > 0；且t t ， j = 1，2……，s-1； （6）
上述模型中，式（2）为汽车容量约束；式（3）保证了每个客户的运输任务仅由一辆车完成，而所有运输任务则由m辆车协同完成；式（4）和式（5）限制了到达和离开某一客户的汽车有且仅有一辆。式（6）对配送时间做了约束，即物品到达指定地点的时间不能大于其最大允许时间。
上述模型中还要考虑时间问题，即每个客户对所送物品的时间要求各不相同，故需加入一个时间参数t 。对每个运输路径都加上时间参数t （t 的值可由客户需求中得知，并记录到数据库。），在每个规定的时间内（如一个月），优先配送t 值小的物品，每次在用遗传算法求解前，遍历规定时间内的所有t ，按照t 值由小到大排列染色体，然后再求出最优解，根据最优解制定配送方案。
三 引入退火算法改进求解过程
针对遗传算法的一些不足，将模拟退火算法与之结合，并加入记忆装置，从而构造了物流配送路径优化问题的一种有记忆功能的遗传模拟退火算法。该算法的特点是扩大了原有遗传算法的搜索邻域，在一定概率控制下暂时接受一些恶化解。同时利用记忆装置保证了在一定终止条件下所得的最终解至少是搜索过程中曾得到所有解中的最优解。该算法通过在常规的遗传算法基础上加入模拟退火算子和记忆装置而得到。下面首先介绍此有记忆功能的遗传模拟算法的步骤。根据参考文献[3],给出下面的算法实现步骤：
STEP1 给定群体规模maxpop，将初始群体按照t 所指定的值进行分块， k=0;初始温度t ＝t ，产生初始群体pop(k)，并且初始群体的每个分块中都具有t 满足某一属性的特征值；对初始群体计算目标值f(i), 找出使函数f (t )最小的染色体i和这个函数值f，记i =i，f =f；其中，f (t )为状态i在温度为t 时的目标值。i∈ pop( k)，即当代群体中的一个染色体；
STEP2 若满足结束条件则停止计算，输出最优染色体i 和最优解f ；否则，在群体pop(k)的每一个染色体i∈ pop(k)的邻域中随机选一状态j∈N( i )，且t 满足条件要求, 按模拟退火中的接受概率
接受或拒绝j，其中f (t )， f (t )分别为状态i，j的目标值。这一阶段共需maxpop次迭代以选出新群体newpop1；
STEP3 在newpop1(k+1)中计算适应度函数
其中，f 是newpop1(k+1)中的最小值。由适应度函数决定的概率分布从newpop1中随机选maxpop个染色体形成种群newpop2；
STEP4 按遗传算法的常规方法对newpop2进行交叉得到crosspop，再变异得到mutpop；
STEP5 染色体中的每个元素在满足t 的情况下，且具有较大t 值的元素完成时没有破坏具有较小t 值进行计算所需条件的情况下，不必按照由小到大的顺序进行排列，
STEP6 令pop(k+1)=mutpop,对pop(k+1)计算f (t ),找出使函数f (t )最小的染色体i和这个函数值f，如果f < f ,则令i = i， f =f， t ＝ d(t )，k = k+1, 返回 STEP2。
出于表示简单，计算机处理方便的目的，对于VRP问题的遗传算法编码通常都采用自然数编码。上述数学模型的解向量可编成一条长度为k＋m＋1的染色体（0，i ，i ，…,i ，0，i ,…i ，0，…0，i ,…,i ，0）。在整条染色体中，自然数 i 表示第 j 个客户。0的数目为m＋1个，代表配送中心，并把自然数编码分为m段，形成m个子路径，表示由m辆车完成所有运输任务。这样的染色体编码可以解释为：第一辆车从配送中心出发，经过i ，i ，…,i 客户后回到配送中心，形成了子路径1；第2辆车也从配送中心出发，途径i ,…i 客户后回到配送中心，形成子路径2。m辆车依次出发，完成所有运输任务，构成m条子路径。
如染色体0123045067890表示由三辆车完成9个客户的运输任务的路径安排：
子路径1：配送中心→客户1→客户2→客户3→配送中心
子路径2：配送中心→客户4→客户5→配送中心
子路径3：配送中心→客户6→客户7→客户8→客户9→配送中心。
为了使算法收敛到全局最优，遗传群体应具有一定的规模。但为了保证计算效率，群体规模也不能太大。一般取群体规模取值在10到100之间。
在初始化染色体时，先生成 k 个客户的一个全排列，再将 m＋1 个 0 随机插入排列中，其中所选的 k 个客户所要求的时间必须在某一个特定的时间段内，且完成任何一个客户配送任务时不能破坏完成其他客户配送任务的条件。需要注意的是必须有两个 0 被安排在排列的头和尾，并且在排列中不能有连续的两个0。这样构成一条满足问题需要的染色体。针对此染色体，随机选择两个位置上的元素进行交换，并用算法对其调整，使其成为新的满足要求的染色体。交换若干次，直至生成满足群体规模数的染色体。
在这里，将容量约束式（2）转为运输成本的一部分，运输成本变为：
其中M为一很大的正数，表示当一辆车的货运量超过其最大载重量时的惩罚系数。M应趋向于无穷大。考虑到计算机处理的问题，参考文献[6]，取M为1000000为宜。将此运输成本函数作为我们的目标函数。适应度函数采用一种加速适应度函数：
这种适应度函数加速性能比较好，可以迅速改进适应度的值，缩短算法运行时间。
将每代种群的染色体中适应度最大的染色体直接复制，进入下一代。种群中其他染色体按其适应度的概率分布，采用轮盘赌的方法，产生子代。这样既保证了最优者可生存至下一代，又保证了其余染色体可按生存竞争的方法生成子代，使得算法可收敛到全局最优。选中的染色体按一定的概率—交叉率，产生子代。交叉率在0.6～0.8之间，算法进化效果较好。
四 试验数据与比较
实验数据取自参考文献[6]。
实验1，随机生成1个有8个门店的VRP问题，初始数据如下：
图1八个门店的需求量及其位置
根据各仓库的需求量，计算出需要的汽车数：m=[17.82/(0.85*8)]+1=3。采用传统的遗传算法的各算子，并对其中的交叉算子进行了改造，取群体规模为20，进化代数为50，应用此程序他费时3s得到的结果为：
而我们的算法在上面的算法中加入了一个模拟退火算子，取初始退火温度为10，衰减系数取0.85使用第三节所述算法步骤，在奔腾四的计算机上计算，耗时2s，得结果如下：
实验2，随机生成1个有20个门店的VRP问题，初始数据如下：
图2 20个门店的需求量及其位置
计算得：需6辆车。用参考文献[6]中的算法取群体规模100，进化代数分别设为20，50，100，得到的结果不同：
图3 普通遗传算法的实验结果
而采用本文的算法，初始退火温度取10，衰减系数取0.85，在奔腾四的计算机上计算，则结果如下：
图4 新型算法的实验结果
从以上两个实验可以看出：采用本文中所述的算法，要得到相同的结果可以缩短进化代数，从而节约运算时间。而要增加进化代数必然得到更好的结果。
五 结论
用模拟退火算法与传统的遗传算法相结合来求解物流系统中车辆路径问题，可以使算法所需的进化代数明显减少，问题解可在最短时间内求出。因此在时间特性上有了比较好的改善，耗时较短，获得了较好的结果。根据参考资料所记载的数据表明，此算法在解决诸如车辆路径问题问题确实可行，并有较好的性能。而且随着问题规模的增大，这种对时间性能的改善效果将更加明显。这就非常有助于物流企业根据自己的实际情况科学、有效的指定物流决策，降低风险，降低成本，提高经济效益和自身的竞争力。
参考文献
[1] 郭耀煌 李军著，车辆优化调度，成都：成都科技大学，1994
[2] 邢文训 谢金星编著，现代优化计算方法，北京：清华大学出版社，1999
[3] 郎茂祥，物流配送车辆调度问题的模型和算法研究，北京：北方交通大学，2002
[4] 郎茂祥 胡思继，用混和遗传算法求解物流配送路径优化问题的研究，中国管理科学，2002
[5] 李军 谢秉磊 郭耀煌，非满载车辆调度问题的遗传算法，系统工程理论与实践，2000
[6] 唐坤，车辆路径问题中的遗传算法设计，东北大学学报（自然科学版），2002
[7] 姜大立 杨西龙 杜文等，车辆路径问题的遗传算法研究，系统工程理论与实践，1999
[8] 阎庆 鲍远律，新型遗传模拟退火算法求解物流配送路径问题，计算机科学与发展，2002 参考技术A http://wenku.baidu.com/view/4e848b17b7360b4c2e3f647c.html?st=1
这是我做的ppt，最后自己编了一个简单的遗传算法代码，实现上面的问题
你应该可以看懂吧!

优化求解基于matlab遗传算法结合粒子群算法求解单目标优化问题含Matlab源码 1659期

一、GA-PSO混合优化算法的基本思想

对于遗传算法来讲, 传统的遗传算法中变异算子是对群体中的部分个体实施随机变异, 与历史状态和当前状态无关。而粒子群算法中粒子则能保持历史状态和当前状态。遗传算法的进化初期, 变异有助于局部搜索和增加种群的多样性;在进化后期, 群体已基本趋于稳定, 变异算子反而会破坏这种稳定。变异概率过大会使遗传模式遭到破坏, 过小又会使搜索过程缓慢甚至停滞不前。本文通过在粒子群算法中引入遗传算法的交叉操作, 改进种群分割策略, 且用粒子群算法重构变异算子来进行算法的改进。本文所提的混合算法主要就是从用遗传算法来模拟粒子群算法的角度出发, 利用粒子群算法来重构遗传算法算子和进行种群分割。从宏观上来看, 其行为是粒子群算法;从微观来看, 其行为是遗传算法, 从而构成遗传-粒子群混合算法。下面主要介绍一下引入的交叉和变异算子及变异算子。

1 交叉算子
设GA-PSO混合算法总的进化代数为T, 当算法进化到第t代时, 总的种群设为∏t=x1t, …, xit, …, xnt, (1≤i≤n) , n为种群规模, xit为单个粒子, 且对于任意i, (1≤i≤n) , 都有xit≤xjt成立, 即∏t有序。由于所讨论的混合算法的个体编码采用了实值编码, 且该算法主要针对于数值优化问题故交叉算子采用了算术交叉。
假设在两个个体xit, xjt (i≠j) 之间进行算术交叉, 则交叉运算后所产生的两个新个体是:

式 (2-1) 中, α为一参数, 若α是一个常数, 此时所进行的交叉运算称为均匀算术交叉;也可以是一个由进化代数决定的变量, 此时进行的是非均匀算术交叉。

2 变异算子
在GA-PSO混合算法中利用粒子群算法的进化公式来重构变异算子, 让个体依据自身迄今最优解和子种群内迄今最优解以及个体进化的速度来决定变异方向和幅度, 使个体在进化的过程中可以将其进化的历史作为导向标。具体实现如下:用xit代替粒子群算法中的xid (第i个粒子在D维空间的位置) , 用∏t中第i位历史最优fimax对应的ximax代替粒子群算法中的Pid (个体最优) , 用子种群的历史最优Fjmax (j为该粒子团在子种群中的位置) 对应的Xjmax代替Pgd (全局最优) , 用ximax的累计差的算术平均Δximax来代替vid。其中ximax的累计差由 (2-2) 式求的:

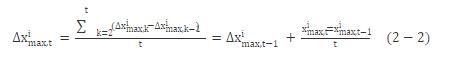
则引入变异算子后的粒子群算法粒子更新公式为

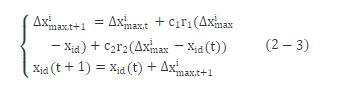
通过上述公式, 我们可以看到在第一部分通过权重因子c1, c2和随机数r1, r2以及信息反馈Ximax预测了变异的幅度和方向;第二部分则具体实施了变异操作。因此, 粒子群算法变异操作具备了自学习能力, 在变异之前的预测, 也使变异操作不再是简单的随机变异, 而是提高单个粒子对进化环境适应能力的变异。

GA-PSO混合优化算法流程图如图2-1,

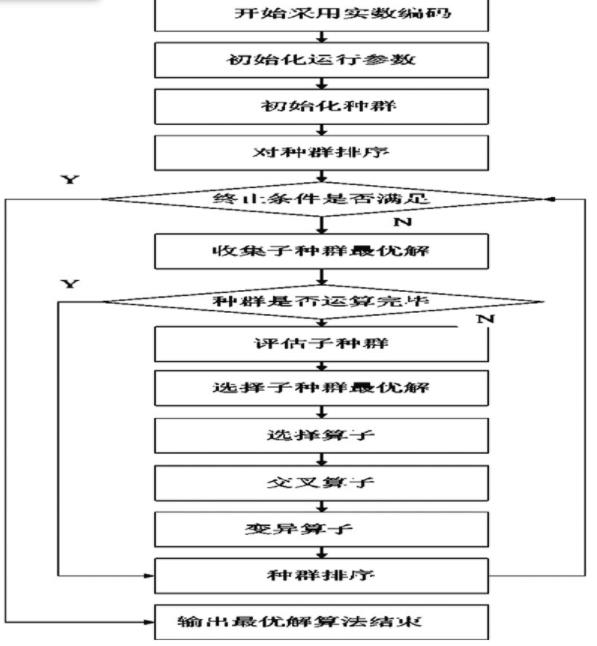
图2-1 GA-PSO流程图

二、部分源代码

%% GA 优化 PSO
%% 清空环境
clc;
clear
close all
%% 参数初始化
lenchrom=7;    %字符串长度（个体长度），染色体编码长度
pc=0.7;        %设置交叉概率，本例中交叉概率是定值，若想设置变化的交叉概率可用表达式表示，或从写一个交叉概率函数，例如用神经网络训练得到的值作为交叉概率
pm=0.3;        %设置变异概率，同理也可设置为变化的

%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=20;   % 进化次数  
popsize=30; %种群规模

%粒子更新速度
Vmax=1;
Vmin=-1;

%种群
popmax=50;
popmin=-50;

% 变量取值范围
bound=[popmin popmax;popmin popmax;popmin popmax;popmin popmax;popmin popmax;popmin popmax;popmin popmax];  %变量范围

% 优化粒子数目
par_num=7;

%% 产生初始粒子和速度
for i=1:popsize
    %随机产生一个种群
    pop(i,:)=popmax*rands(1,par_num);    %初始种群
    V(i,:)=rands(1,par_num);  %初始化速度
    %计算适应度
    fitness(i)=fun(pop(i,:));   %染色体的适应度
end

%找最好的染色体
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    i
    for j=1:popsize
        
        %速度更新 PSO选择更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        
        %种群更新 PSO选择更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)<popmin))=popmin;
        
        % 交叉操作 GA
        GApop=Cross(pc,lenchrom,pop,popsize,bound);
        
        % 变异操作 GA变异
        GApop=Mutation(pm,lenchrom,GApop,popsize,[i maxgen],bound);
        
        pop=GApop; % GA pop --> PSO pop
      
        % 适应度值 --> 约束条件
         if 0.072*pop(j,1)+0.063*pop(j,2)+0.057*pop(j,3)+0.05*pop(j,4)+0.032*pop(j,5)+0.0442*pop(j,6)+0.0675*pop(j,7)<=264.4
            if 128*pop(j,1)+78.1*pop(j,2)+64.1*pop(j,3)+43*pop(j,4)+58.1*pop(j,5)+36.9*pop(j,6)+50.5*pop(j,7)<=69719
                    fitness(j)=fun(pop(j,:));
               end
         end

        %个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j) < fitnesszbest
            zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
        
    end
    
    yy(i)=fitnesszbest;     
end

%% 结果
disp '*************best particle number****************'
zbest

%%
plot(yy,'linewidth',2);
grid on
title(['适应度曲线  ' '终止代数＝' num2str(maxgen)]);
xlabel('进化代数');ylabel('适应度');

三、运行结果

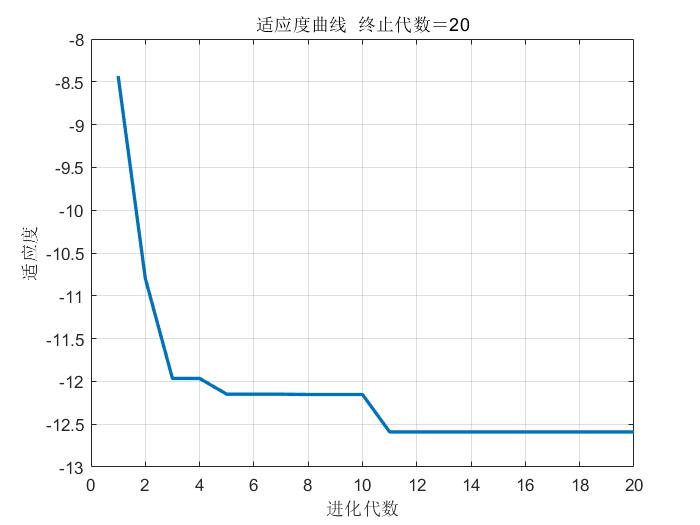
四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]包子阳,余继周,杨杉著.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社
[2]巩永光.粒子群算法与遗传算法的结合研究[J].济宁学院学报. 2008,29(06)