最小生成树之KruskaI算法，用并查集判断是否有环

Posted 2023-01-02 覃会程

最小生成树的概念：

• ➢连通图去一条边就是树
  
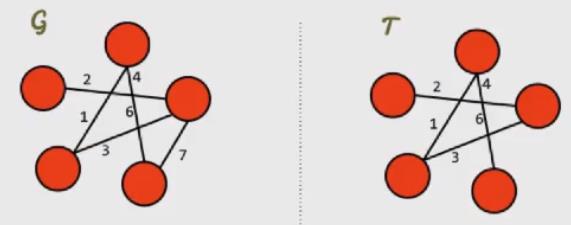
• ➢所有生成树中边的权重和最小的，称之为最小生成树( Minimal Spanning Tree )
  
• ➢常用于网络构建等建设性问题的优化

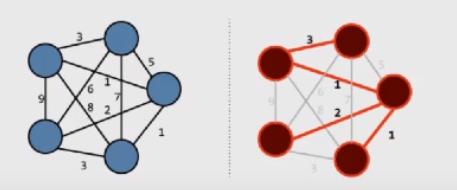
算法实现思路：

1. 先将带权的边进行升序排序。
2. 按照从小到大的顺序取出边，拿的时候判断边所连接的两个节点是否在同一个集合，如果两个节点不在一个集合则放弃这一条边，开始下一条边的判断。（这是为了避免出现环）。
3. 刚开始时，每一个节点都是一个独立的集合，到取出一条边时，将这条边对应的两个顶点对应的两个集合合并成一个集合。加上第二步的判断就可以保证取出的边不会形成环；因为同一个集合的边都在一条线上，如果给一条边上的两个节点增加一条边就会出现环。
4. 当取出的边等于节点数-1时，则结束；这时，取出的所有边都就构成的最小生成树。

并查集

• 上面用是否在同一个集合的方法判断是否出现环；实际上是用的就是并查集算法；可以用一颗树表示一个集合，用树的根节点作为集合的标志。

• 刚开始所有节点都是一颗独立的树，当将两个节点合并时，可以选择其中一个节点作为树的根节点（即让一个节点指向另一个），当合并的是两颗树时，可以将其中一棵树的根节点指向另一棵树。当需要查找某一个节点所在的集合时，可以通过该节点一直向上找根节点，然后将根节点返回即可确定节点所在的集合。

• 并查集最主要就是将集合合并的函数和查找节点所在集合的函数。

并查集可以用一个一维数组实现，算法的步骤如下：

1. 创建一个大小为n的一维数组，n是节点的个数，数组下标的表示第几个节点，数组元素表示对应节点的父节点。
2. 将数组初始化为-1，-1表示该节点没有父节点，即该节点是一个根节点。
3. 将两个节点对应的集合进行合并，即将两颗树进行合并，先找出两颗子树根节点，然后将其中一个根节点指向另一个根节点。

代码如下：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.HashSet;
import java.util.List;
import java.util.Set;

public class 最小生成树 
	
	static int[] parent = new int[5];//存储每一个节点的父节点
	
	public static void main(String[] args) 
		//初始化图
		List<Edge> l = new ArrayList<Edge>();
		l.add(new Edge('C','D',1));
		l.add(new Edge('C','A',1));
		l.add(new Edge('C','E',8));
		l.add(new Edge('A','B',3));
		l.add(new Edge('D','E',3));
		l.add(new Edge('B','C',5));
		l.add(new Edge('B','E',6));
		l.add(new Edge('B','D',7));
		l.add(new Edge('A','D',2));
		l.add(new Edge('A','E',9));
		Collections.sort(l);  //对边进行排序
		
		Arrays.fill(parent, -1);  //将数组初始化为-1
		
		Set<String> s = new HashSet<String>(); //用于存储选中的边
		int count = 0;  //用于统计取出边的数量
		
		//依次添加四条边
		for(int i=0; count<5-1; i++)
			Edge temp = l.get(i);
			if(!union(temp.start,temp.end))
				continue;
			
			String str = (char)(temp.start+'A') + "--" +(char)(temp.end+'A'); 
			s.add(str);
			count++;
		
		
		//打印结果
		for(String str:s)
			System.out.println(str);
		
		
	
	//查找节点所在的集合（查找根节点）
	private static int findRoot(int t)
		int res = t;
		while(parent[res]!=-1)
			res = parent[res];
		
		return res;
	
	
	//将两个节点所在的树（集合）进行合并; 合并失败返回false，成功返回true
	//同时也可以检查两个节点是否在同一个集合
	private static boolean union(int x, int y)
		int xroot = findRoot(x);
		int yroot = findRoot(y);
		if(xroot == yroot)   //两个节点在同一颗树
 			return false;
		
		parent[xroot] = yroot; //将x的根节点指向y的根节点
		return true;
	


class Edge implements Comparable<Edge>
	int start;  //边的起点
	int end;    //边的终点
	int distance; //边的权值
	
	public Edge(char start, char end, int distance) 
		super();
		this.start = (int)(start-'A');  //将字符转换为int类型
		this.end = (int)(end-'A');
		this.distance = distance;
	

	@Override
	public int compareTo(Edge o)   //返回正数表示this会排在后面
		if(this.distance>o.distance)
			return 1;
		
		if(this.distance<o.distance)
			return -1;
		
		return 0;