如何求解一个矩阵的特征向量?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何求解一个矩阵的特征向量?相关的知识,希望对你有一定的参考价值。
参考技术A 把特征值代入特征方程,运用初等行变换法,将矩阵化到最简,然后可得到基础解系。求矩阵的全部特征值和特征向量的方法如下:第一步:计算的特征多项式;
第二步:求出特征方程的全部根,即为的全部特征值;
第三步:对于的每一个特征值,求出齐次线性方程组:的一个基础解系,则可求出属于特征值的全部特征向量。
扩展资料
求特征向量:
设A为n阶矩阵,根据关系式Ax=λx,可写出(λE-A)x=0,继而写出特征多项式|λE-A|=0,可求出矩阵A有n个特征值(包括重特征值)。将求出的特征值λi代入原特征多项式,求解方程(λiE-A)x=0,所求解向量x就是对应的特征值λi的特征向量。
判断矩阵可对角化的充要条件:
矩阵可对角化有两个充要条件:
1、矩阵有n个不同的特征向量;
2、特征向量重根的重数等于基础解系的个数。对于第二个充要条件,则需要出现二重以上的重特征值可验证(一重相当于没有重根)。
若矩阵A可对角化,则其对角矩阵Λ的主对角线元素全部为A的特征值,其余元素全部为0。(一个矩阵的对角阵不唯一,其特征值可以换序,但都存在由对应特征向量顺序组成的可逆矩阵P使P⁻¹AP=Λ)。
求矩阵特征值的方法如下:
任意一个矩阵A可以分解成如下两个矩阵表达的形式:
其中矩阵Q为正交矩阵,矩阵R为上三角矩阵,至于QR分解到底是怎么回事,矩阵Q和矩阵R是怎么得到的,你们还是看矩阵论吧,如果我把这些都介绍了,感觉这篇文章要写崩,或者你可以先认可我是正确的,然后往下看。
由式(22)可知,A1和A2相似,相似矩阵具有相同的特征值,说明A1和A2的特征值相同,我们就可以通过求取A2的特征值来间接求取A1的特征值。
numpy求解特征值和特征向量
特征值和特征向量
特征值就是方程Ax=ax的根, 是一个标量
特征向量是关于特征值的向量
Key_Function
np.linalg.eigvals函数, 计算矩阵的特征值
np.linalg.eig函数, 返回包含特征值和对应的特征向量的元组
Code
import numpy as np A = np.mat("1 -2 1; 0 2 -8; -4 5 9") print(A) ‘‘‘ [[ 1 -2 1] [ 0 2 -8] [-4 5 9]] ‘‘‘ b = np.array([0, 8, -9]) print(b) ‘‘‘ [ 0 8 -9] ‘‘‘ x = np.linalg.solve(A, b) print(x) # [ 29. 16. 3.] print(np.dot(A, x)) # [[ 0. 8. -9.]]
数学概念
对于给定矩阵A,寻找一个常数λ(可以为复数)和非零向量x,使得向量x被矩阵A作用后所得的向量Ax与原向量x平行,并且满足Ax=λx。
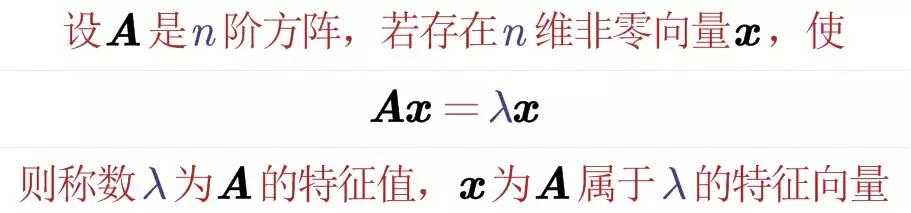
以上是关于如何求解一个矩阵的特征向量?的主要内容,如果未能解决你的问题,请参考以下文章