Keras深度学习实战（42）——强化学习基础

Posted 2022-12-28 盼小辉丶

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Keras深度学习实战（42）——强化学习基础相关的知识，希望对你有一定的参考价值。

Keras深度学习实战（42）——强化学习基础

0. 前言

强化学习是当前人工智能领域的研究热点问题，强化学习主要通过考察智能体与环境的相互作用，得到策略模型、优化策略并最大化累积回报的过程。强化学习具有巨大的研究价值和应用潜力，是实现通用人工智能的关键技术。本文首先介绍强化学习的基本原理，包括马尔可夫决策过程、价值函数、探索-利用问题等，然后介绍经典的强化学习算法，最后使用 Keras 实现在游戏中模拟强化学习算法。

1. 强化学习基础

1.1 基本概念

强化学习的核心思想在于最大化智能体在相应环境中得到的累计奖励，从而学习能够令智能体完成目标任务的最佳策略。智能体 (agent) 在每个时刻可以与环境 (environment) 交互，交互过程如下所示：

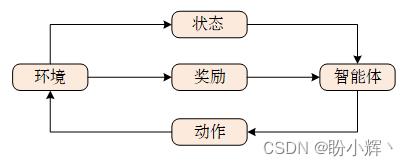
每次交互，都可以得到一个具有多维特征的观察 (observation)，根据观察可以得到状态 (state)，智能体根据状态选择相应的动作 (action)，环境会对 agent 的不同动作给予不同奖励 (reward)，从状态到动作的映射函数称为策略 (policy)。通过重复执行此过程，就可以得到令累计奖励最大化的最佳策略。

1.2 马尔科夫决策过程

智能体从环境初始状态开始，根据策略模型采样某一动作，环境在动作的影响下，会从原状态改变为新状态，同时给予智能体奖励。以上过程不断重复直到达到游戏的终止状态，这个过程也称为轨迹 (trajectory)，一个过程称为一个回合 (episode)。环境的当前状态通常取决于多个历史状态，计算非常复杂，为了简化计算流程，我们通常假设当前时间戳上的状态仅仅受上一状态的影响，这种性质称为马尔科夫性 (Markov Property)，具有马尔科夫性的序列称为马尔科夫过程 (Markov Process)。
如果我们将执行的动作也考虑进状态转移概率，同样应用马尔科夫假设，当前状态只与上一状态和上一状态上执行的动作相关，则我们把状态和动作的有序序列叫做马尔科夫决策过程 (Markov Decision Process, MDP)。当智能体只能观察到环境的部分状态时，称为部分可观察马尔可夫决策过程 (Partially Observable Markov Decision Process , POMDP)

1.3 目标函数

智能体每次在与环境进行交互时，都会得到一个奖励，一次交互轨迹的累计奖励称为总回报 (return)，但在某些环境中的奖励是十分稀疏的，例如在棋牌类游戏中，前面的动作奖励均为 0，只有游戏结束时才有表示输赢的奖励。为了权衡近期奖励与长期奖励，引入折扣率来令奖励随时间衰减。
由于环境状态转移和策略具有一定的随机性，即使使用同样的策略模型作用域同一环境，也可能产生截然不同的轨迹序列，因此强化学习的目标是最大化期望回报。

2. 在具有非负奖励的模拟游戏中获取最佳动作

在本节中，我们将了解如何在模拟游戏中采取正确动作，主要目的是进一步介绍强化学习的工作原理。

2.1 问题设定

我们首先定义环境，用于之后运行模拟。假设，有三个格子，两个玩家在上面玩游戏，初始时空白格子如下：

玩家 1 用 1 标记一个方格，而玩家 2 用 2 标记一个方格，能够标记两个连续方格的玩家获胜，对于此问题，只有玩家 1 有机会赢得比赛。玩家 1 获胜的可能情况如下：

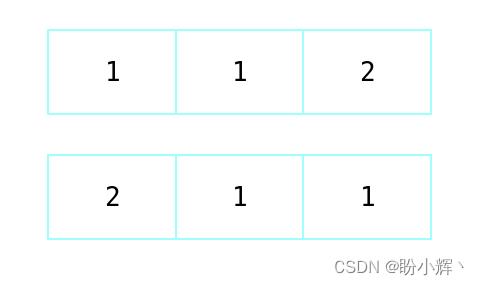
从问题定义中可以看出，玩家 1 获胜的方式是选择标记中间的格子。这样，不管玩家 2 选择哪个格子，玩家 1 都将在其后续操作时获胜。

2.2 模型分析

尽管玩家 1 取得胜利的动作显而易见，但对于计算机而言却并非如此。接下来，我们将了解智能体如何自动找出最佳动作。我们将采用以下策略来解决此问题：

初始时空白格子
玩家 1 随机选择一个盒子
玩家 2 从剩余的 2 个盒子中随机选择一个盒子
根据玩家 1 留下的盒子，我们更新玩家 1 的奖励：
- 如果玩家 1 能够在两个连续的盒子中放置 1，则他是获胜者，将获得奖励 1
- 否则，玩家 1 将获得奖励 0
重复以上过程 100 次，在其中进行游戏，并存储每次的奖励
计算所采取的不同策略中第一步的平均奖励
第一步中选择的，在 100 次迭代中具有最高平均奖励的格子是玩家 1 第一步的最佳动作。

2.3 模型构建与训练

(1) 定义游戏环境和进行游戏的函数，在函数中，初始化一个全为 0 值的空白格子。在迭代过程中，每次生成一个名为 samp 的随机动作，玩家 1 采取第一个动作，然后玩家 2 采取第二个动作，最后一个步骤是玩家 1 采取动作，我们按此步骤填充空白格子：

import random

def play_game():
    empty_board = [0,0,0]
    move = []
    for step in range(3):
        index_to_choose = [i for i,j in enumerate(empty_board) if j==0]
        samp = random.sample(range(len(index_to_choose)), 1)[0] 
        if(step%2==0):
            empty_board[index_to_choose[samp]]=1
            move.append(index_to_choose[samp])
        else:
            empty_board[index_to_choose[samp]]=2 
    return(reward(empty_board), move[0])

(2) 定义函数 reward 以在游戏结束时计算奖励：

def reward(empty_board):
    reward = 0
    if((empty_board[0]==1 & empty_board[1]==1)|(empty_board[1]==1 & empty_board[2]==1)):
        reward = 1
    else:
        reward = 0
    return reward

(3) 进行 100 回合游戏：

rew = []
step = []
for i in range(100):
    r, move = play_game()
    rew.append(r)
    step.append(move)

(4) 计算在第一步中选择不同动作的奖励，可以看到在第一步中占据第二个格子时平均奖励最高：

sub_list = [i for i,j in enumerate(step) if j==1]
final_reward = 0
count = 0
for i in sub_list:
    final_reward += rew[i]
    count+=1
print(final_reward/count)

3. 在模拟游戏中获取最佳动作

在上一节中，我们使用了一个简单问题，即在达到目标时会得到奖励。我们可以定义一个稍微复杂的游戏，在环境中既有正奖励又有负奖励，但目标相同是最大化奖励。

3.1 问题定义

我们使用以下环境，从包含 S 的单元格开始，目标是到达奖励为 +1 的单元格：

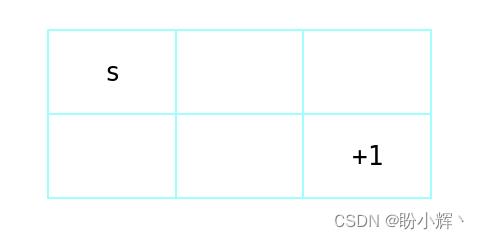
为了最大化获得奖励的概率，使用 Bellman 方程，该方程可以计算网格中每个单元的值：

当前单元格的值 = 从当前单元格移动到下一个单元格的奖励 + 折扣因子 * 下一个单元格的值

在此问题中，移动到奖励为 +1 的单元格以外的单元格的奖励为 0，与其他单元格相比，远离目标单元格的单元格具有较低的值。一旦计算了每个单元格的值，智能体就可以移动到的所有单元格中具有最高值的单元格。

3.2 模型分析

我们用于计算每个单元格值的策略如下：

初始化一个空白网格
定义智能体可以在单元格中执行的动作
定义智能体在当前单元格中执行的动作后将进入的下一状态
计算当前状态的值，该值取决于移动到下一个状态的奖励以及下一个状态的值
根据以上计算更新当前状态的单元格值
存储在当前状态下执行的动作以移至下一个状态
在迭代起始阶段，远离最终目标单元格的值为零，而与最终状态相邻的单元格的值则逐渐增加
多次迭代更新单元格值，从而能够确定智能体遵循的最佳路线

3.3 模型构建与训练

(1) 初始化一个空网格，并定义可以在不同状态下执行的操作，其中 D 表示向下移动，R 表示向右移动，L 表示向左移动，U 表示向上移动：

empty_board = [[0,0,0]
             ,[0,0,1]]

state_actions = (0,0):('D','R')
                 ,(0,1):('D','R','L')
                 ,(0,2):('D','L')
                 ,(1,0):('U','R')
                 ,(1,1):('L','U','R')

(2) 定义函数，用于返回在给定当前状态下采取动作后的将进入的下一状态：

def get_next_state(curr_state, action):
    i,j = curr_state
    if action=='D':
        i = i+1
    elif action=='U':
        i = i-1
    elif action=='R':
        j = j+1
    elif action=='L':
        j = j-1
    else:
        print('unk')
    return((i,j))

(3) 初始化用于存储状态、动作和奖励的列表：

def print_values():
    print(empty_board[:][0])
    print(empty_board[:][1])
curr_state = (0,0)
state_action_reward = []
state = []
state_action = []

(4) 在一个回合中最多执行 100 个动作，在一个单元格(状态)中采取随机动作，并根据移动到下一个状态的奖励以及下一状态值计算当前状态的值。重复迭代以上步骤 100 次(回合)，在一个状态中采取随机动作，然后进入下一个状态，并计算每个单元格的值：

for m in range(100):
    curr_state = (0,0)
    for k in range(100):
        reward = 0
        action = state_actions[curr_state][random.sample(range(len(state_actions[curr_state])),1)[0]]
        next_state = get_next_state(curr_state, action)
        state.append(curr_state)

        empty_board[curr_state[0]][curr_state[1]] = reward + \\
                    empty_board[next_state[0]][next_state[1]]*0.9 
        
        curr_state = next_state
        state_action.append(action)

        if(next_state==(1,2)):
            reward+=1
        break
    if(m%10==0):
        print('==========')
        print_values()

运行代码后，得到的每个单元格的最终值如下所示：

[0.7290000000000001, 0.0523347633027361, 0.38742048900000015]
[0.5314410000000002, 0.9, 1]

从输出结果来看，智能体可以在游戏开始时最好采取向下的动作，因为下方单元格的值高于右侧单元格的值。

(5) 进一步，我们可以考虑使用以下环境：

empty_board = [[0,0,-1]
             ,[0,0,1]]

(6) 在不同状态可以采取的动作如下：

state_actions = (0,0):('D','R')
                 ,(0,1):('D','R')
                 ,(1,0):('R')
                 ,(1,1):('R')

(7) 多次迭代后，计算各个单元格中的单元格状态值：

curr_state = (0,0)
state_action_reward = []
state = []
state_action = []

for m in range(100):
    curr_state = (0,0)
    for k in range(100):
        reward = 0
        action = state_actions[curr_state][random.sample(range(len(state_actions[curr_state])),1)[0]]
        next_state = get_next_state(curr_state, action)
        state.append(curr_state)
            
        empty_board[curr_state[0]][curr_state[1]] = reward + empty_board[next_state[0]][next_state[1]]*0.9 
        
        curr_state = next_state
        state_action.append(action)
        
        if(next_state==(0,2)):
            break
        if(next_state==(1,2)):
            break
    if(m%10==0):
        print('==========')
        print_values()

结果值如下所示：

[-0.81, -0.9, -1]
[0.81, 0.9, 1]

从以上结果可以看出，智能体从左上角执行向下的动作比向右要好，因为下方单元格的状态值更高。

小结

在未知环境中，研究智能体的学习行为是一个既充满挑战又有趣的问题，强化学习通过试探与环境交互获得策略的改进，是机器学习研究中的一个重要分支。本文首先讲解了强化学习的基本概念与重要背景知识，然后利用 Keras 模拟了两个简单的游戏环境，从而加深对强化学习原理的理解。

系列链接

以上是关于Keras深度学习实战（42）——强化学习基础的主要内容，如果未能解决你的问题，请参考以下文章

Keras深度学习实战（13）——目标检测基础详解

Keras深度学习实战——神经网络基础与模型训练过程详解

PyTorch强化学习实战——强化学习环境配置与PyTorch基础

Keras深度学习实战——使用Keras构建神经网络

学习Keras:《Keras快速上手基于Python的深度学习实战》PDF代码+mobi

深度学习框架Keras介绍及实战