深度学习中的卷积操作

Posted 2022-12-16 zyw2002

本文从信号处理中的互相关运算引入深度学习中的卷积。
然后介绍了不同的卷积类型，以及如何在pytorch中使用这些卷积层。

（在看pytorch文档中的Conv1D/2D/3D的时候感到比较困惑，又很好奇深度学习中各种各样的卷积操作。于是结合整理几乎包含深度学习中所有的卷积操作，主要参考的有《Dive into Deep learning》, cs231, pytorch的官网文档，stackoverflow以及csdn和知乎上的介绍…简单记录一下）

文章目录

• • 本文从信号处理中的`互相关运算`引入`深度学习中的卷积`。 然后介绍了`不同的卷积类型`，以及如何在`pytorch`中使用这些卷积层。
• 一、前言
• • 1.1 数学中的卷积操作
  • 1.2 信号处理中的互相关运算
• 二、深度学习中的卷积
• • 2.1 卷积操作
  • 2.2. 填充和步幅
  • • Padding
    • Stride
  • 2.3 多输入通道和多输出通道
  • • 多输入通道
    • 多输出通道
• 三、卷积类型
• • 3.1 1D/2D/3D 卷积
  • • 1D 卷积
    • 2D卷积
    • 3D卷积
  • 3.2 1x1卷积
  • 3.3 转置卷积 （反卷积）
  • • 1D反卷积
    • 2D反卷积
    • 3D反卷积
  • 3.4 扩张卷积（空洞卷积）
  • 3.5 可分离卷积
  • • 空间可分离卷积
    • 深度可分离卷积
  • 3.6 扁平卷积
  • 3.7 分组卷积
• 参考

一、前言

1.1 数学中的卷积操作

图像中的卷积操作由数学中卷积的演化而来，所以我们先了解下数学中的卷积操作

---

直观理解：
在信号/图像处理中，卷积定义为
两个函数在反转和移位后的乘积的积分，以下可视化展示了这一过程：

---

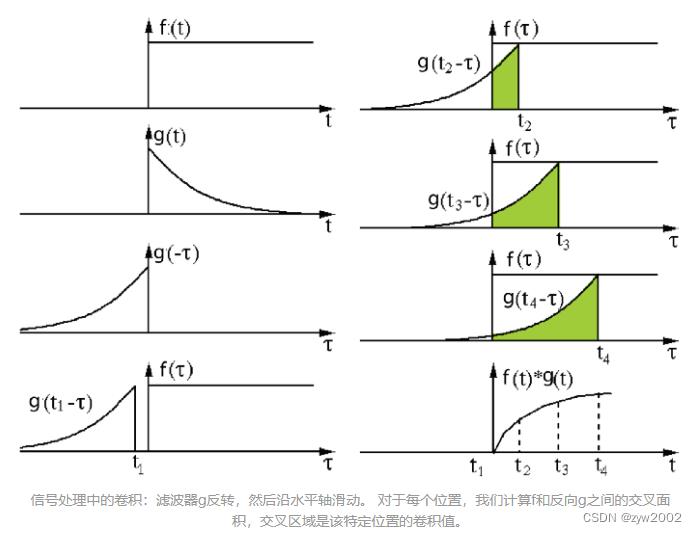
数值理解：

• 连续函数的卷积
  在数学中, 两个函数（比如 $f,g$ : ${\mathbb{R}}^d\to \mathbb{R}$ ）之间的 “卷积”被定义为
  $$(f\ast g)(\mathbf{x})=\int f(\mathbf{z})g(\mathbf{x}-\mathbf{z})d\mathbf{z}.$$
  也就是说, 卷积是当把函数g “翻转” 并移位$\mathbf{x}$时, 测量$f$和$g$之间的乘积。
• 离散函数的卷积
  当为离散对象时, 积分就变成求 和。例如：对于由索引为$\mathbb{Z}$的、平方可和的、无限维向量集合中抽取的向量，我们得到以下定义：

$$(f\ast g)(i)=\sum _{a}f(a)g(i-a).$$

• 二维函数的卷积
  对于二维张量, 则为$f$的索引$(a,b)$和$g$的索引$(i-a,j-b)$上的对应加和:
  $(f\ast g)(i,j)={\sum }_a{\sum }_{b}f(a,b)g(i-a,j-b).$

1.2 信号处理中的互相关运算

严格来说，卷积层是个错误的叫法，因为它所表达的运算其实是互相关运算（cross-correlation），⽽不是卷积运算。在卷积层中，输⼊张量和核张量通过互相关运算产⽣输出张量。

---

直观理解：
互相关被称为滑动点积或两个函数的滑动内积。互相关的filters不需要反转，它直接在函数f中滑动。f和g之间的交叉区域是互相关，下图显示了相关性和互相关之间的差异：

---

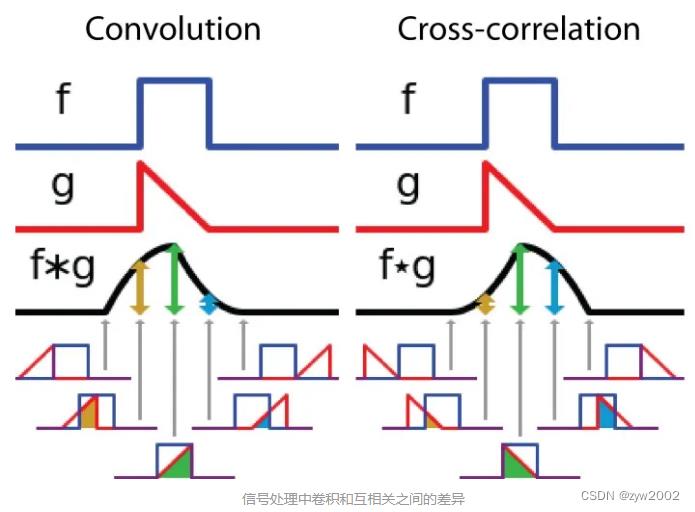
数值理解:
在深度学习中，卷积中的filters是不需要反转的。严格来说，它们是互相关的，本质上是执行逐元素的乘法和加法，在深度学习中我们称之为卷积。

二、深度学习中的卷积

2.1 卷积操作

我们先以最简单的单通道的卷积为例，来讲解深度学习中的卷积操作~

---

单通道的卷积操作：
首先，我们使用3x3滤波器进行二维卷积运算：
左边是卷积层的输入，例如输入图像。右边是卷积滤波器(Filter)，也叫核(Kernel)。由于滤波器的形状是3x3，这被称为3x3卷积。

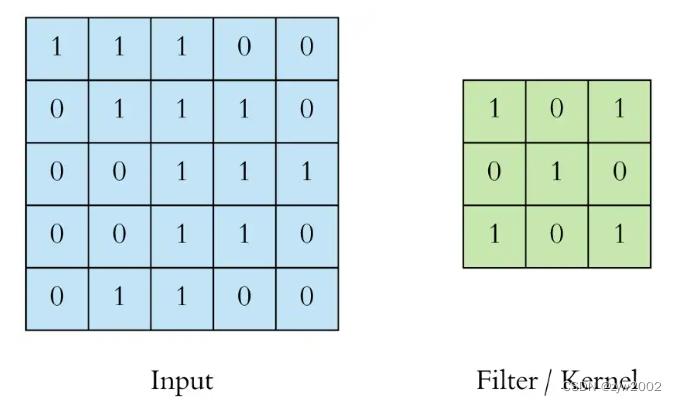
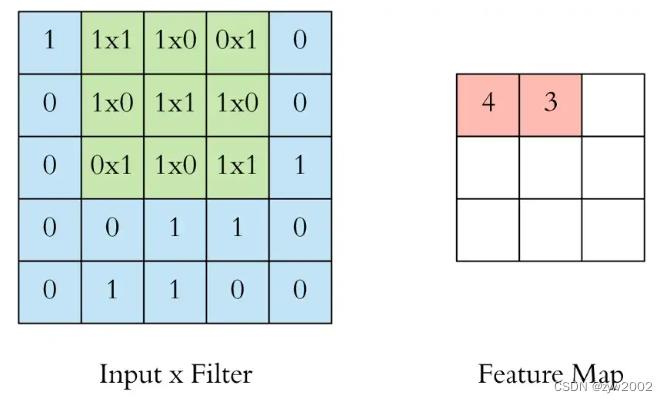
我们通过在输入上滑动这个滤波器来执行卷积运算。在每个位置，我们都进行逐元素矩阵乘法并对结果求和。这个总和进入特征图（feature map）。卷积运算发生的绿色区域被称为感受野(receptive field)。由于滤波器的大小，感受野也是3x3。

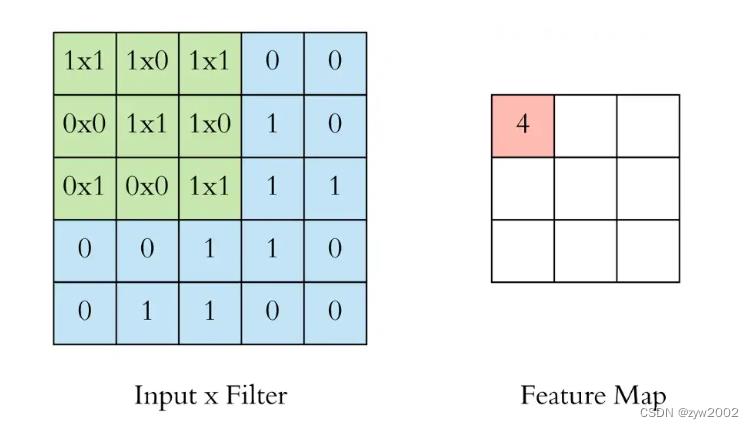
这里的卷积核在左上角，卷积运算“4”的输出显示在结果的特征图中。
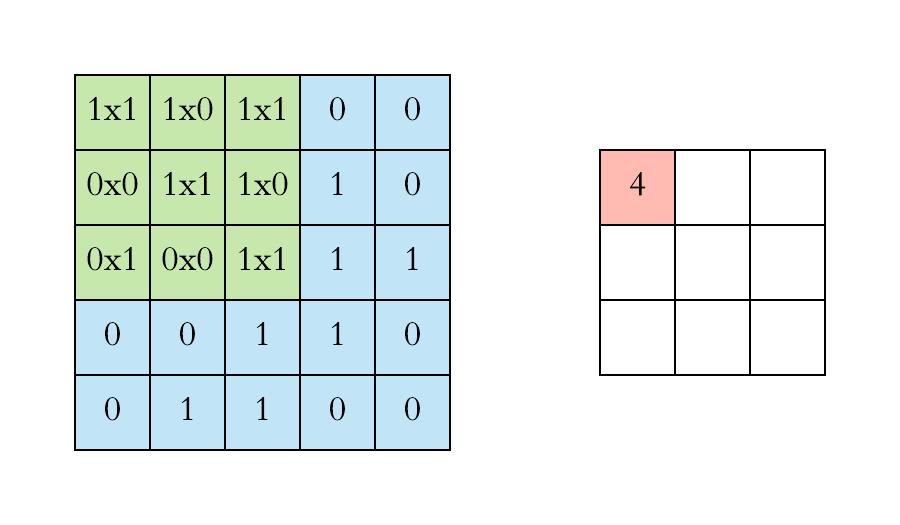
然后我们将滤波器向右滑动并执行相同的操作，将结果也添加到特征映射中。

我们继续这样做，并在特征图中聚合卷积结果。下面的动画展示了整个卷积运算。

2.2. 填充和步幅

Padding

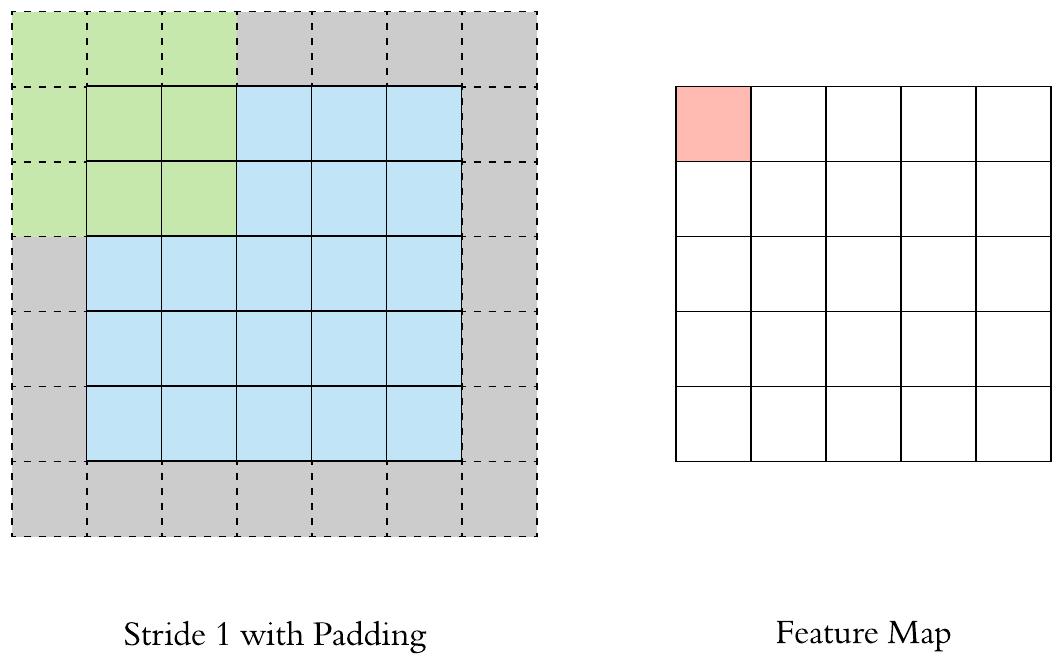
在应用多层卷积时，我们常常丢失边缘像素。 由于我们通常使用小卷积核，因此对于任何单个卷积，我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层，累积丢失的像素数就多了。 解决这个问题的简单方法即为填充（padding）

在输入图像的边界填充元素（通常填充元素是0）的方法叫做填充。

---

先看个动画直观感受下~ 灰色的区域是填充的地方

---

再来看看带填充的二维互相关运算~

通常, 如果我们添加$p_h$行填充 (大约一半在顶部, 一半在底部）和$p_w$列填充（左侧大约 一半, 右侧一半）, 则输出形状将为

$$\left(n_h-k_h+p_h+1\right)\times \left(n_w-k_w+p_w+1\right)。$$
这意味着输出的高度和宽度将分别增加 $p_h$ 和$p_w$ 在许多情况下, 我们需要设置$p_h=k_h-1$ 和$p_w=k_w-1$, 使输入和输出具有相同的高 度和宽度。这样可以在构建网络时更容易地预测每个图层的输出形状。假设$k_h$是奇数, 我们将在高度的两侧填充$p_h/2$行。如果$k_h$是偶数, 则一种可能性是在输入顶部填充$\lceil p_h/2\rceil$行, 在底部填充$\lfloor p_h/2\rfloor$行。同理, 我们填充宽度的两侧。

卷积神经网络中卷积核的高度和宽度通常为奇数，例如1、3、5或7。 选择奇数的好处是，保持空间维度的同时，我们可以在顶部和底部填充相同数量的行，在左侧和右侧填充相同数量的列。

此外，对于任何二维张量X，当满足： 1. 卷积核的大小是奇数； 2. 所有边的填充行数和列数相同； 3. 输出与输入具有相同高度和宽度 则可以得出：输出Y[i, j]是通过以输X[i, j]为中心，与卷积核进行互相关计算得到的。

Stride

在计算互相关时，卷积窗口从输入张量的左上角开始，向下、向右滑动。 在前面的例子中，我们默认每次滑动一个元素。 但是，有时候为了高效计算或是缩减采样次数，卷积窗口可以跳过中间位置，每次滑动多个元素。

我们将每次滑动元素的数量称为步幅（stride）。

---

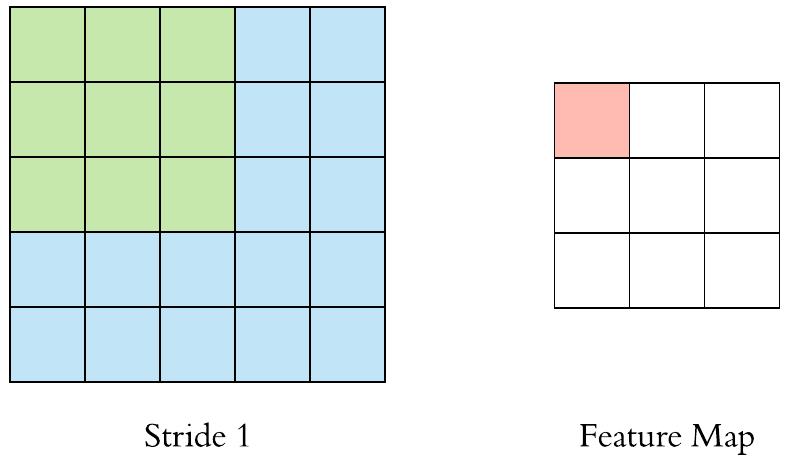
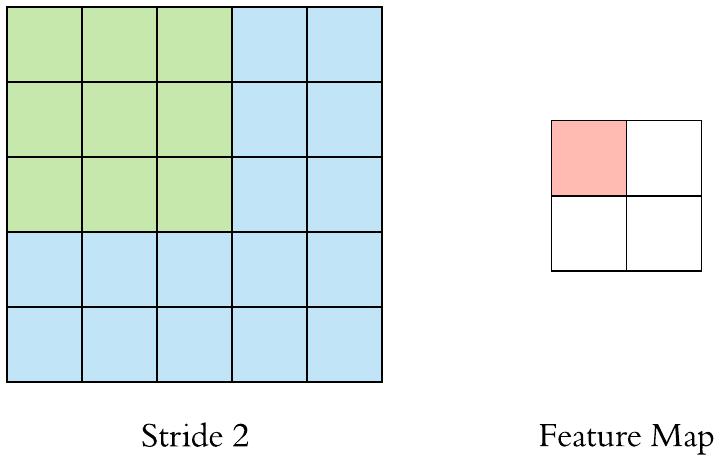
先看个动画直观感受下~ 注意观察stride变大时，输出的特征图变小

• stride =1
  
• stride=2
  

---

再来看看不同步幅的二维互相关运算~
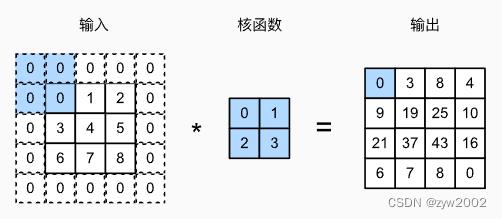
下图是垂直步幅为3，水平步幅为2的二维互相关运算。
着色部分是输出元素以及用于输出计算的输入和内核张量元素：0×0+0×1+1×2+2×3=8、0×0+6×1+0×2+0×3=6。

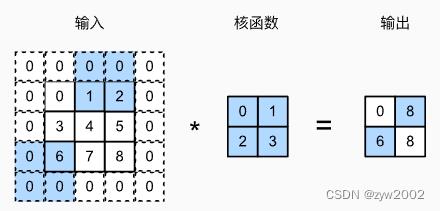
可以看到，为了计算输出中第一列的第二个元素和第一行的第二个元素，卷积窗口分别向下滑动三行和向右滑动两列。但是，当卷积窗口继续向右滑动两列时，没有输出，因为输入元素无法填充窗口（除非我们添加另一列填充）
通常, 当垂直步幅为$s_h$ 、水平步幅为$s_w$时, 输出形状为

$$\lfloor \left(n_h-k_h+p_h+s_h\right)/s_h\rfloor \times \lfloor \left(n_w-k_w+p_w+s_w\right)/s_w\rfloor .$$

如果我们设置了$p_h=k_h-1$和$p_w=$

读书报告--04神经网络基础学习

深度学习笔记-VGG

深度学习笔记-VGG（池化）

深度学习：基于python：第7章 卷积神经网络

深度学习中CNN的窗口大小如何选择？

深度学习中的卷积操作