《异常检测——从经典算法到深度学习》20 HotSpot：多维特征 Additive KPI 的异常定位

Posted 2022-12-15 smile-yan

《异常检测——从经典算法到深度学习》

• 0 概论

• 1 基于隔离森林的异常检测算法

• 2 基于LOF的异常检测算法

• 3 基于One-Class SVM的异常检测算法

• 4 基于高斯概率密度异常检测算法

• 5 Opprentice——异常检测经典算法最终篇

• 6 基于重构概率的 VAE 异常检测

• 7 基于条件VAE异常检测

• 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测

• 9 异常检测资料汇总（持续更新&抛砖引玉）

• 10 Bagel: 基于条件 VAE 的鲁棒无监督KPI异常检测

• 11 ADS: 针对大量出现的KPI流快速部署异常检测模型

• 12 Buzz: 对复杂 KPI 基于VAE对抗训练的非监督异常检测

• 13 MAD: 基于GANs的时间序列数据多元异常检测

• 14 对于流数据基于 RRCF 的异常检测

• 15 通过无监督和主动学习进行实用的白盒异常检测

• 16 基于VAE和LOF的无监督KPI异常检测算法

• 17 基于 VAE-LSTM 混合模型的时间异常检测

• 18 USAD：多元时间序列的无监督异常检测

• 19 OmniAnomaly：基于随机循环网络的多元时间序列鲁棒异常检测

• 20 HotSpot：多维特征 Additive KPI 的异常定位
  相关：

• VAE 模型基本原理简单介绍

• GAN 数学原理简单介绍以及代码实践

• 单指标时间序列异常检测——基于重构概率的变分自编码（VAE）代码实现（详细解释）

20. HotSpot：多维特征 Additive KPI 的异常定位

论文下载：netman | ieee.org 下载后排版有一定偏差，但内容相同。
论文发表于 IEEE Access 2018
源码地址：暂时没有找到源码

20.1 论文概述

首先必须说明的是，该论文提出的算法与本系列其他算法有很大的不同，包括：

• 相对与异常检测 工作，更加注重的是 异常定位；
• 数据对象为 Additive多维特征 KPI 数据 （什么事 Additive KPI 在后面介绍）

20.1.1 论文提出算法的动机是什么？应用于什么场景？（Motivation）

当异常发生后，我们需要找到异常发生的根因（root cause），也就是定位到具体哪个KPI表现出异常，即找出根本原因。

这里举个例子，对于某一个特定业务，需要用到的中间件包括 mysql, redis, es，对应的微服务包括 service1, service2，我们对提供服务的各个阶段都采集 KPI 数据，当异常发生时，我们需要快速找到究竟是谁出了问题。这里需要强调 root cause 的含义，当我们发现某个服务模块有问题而这个服务模块包括 redis 与 mysql 以及服务提供逻辑代码，我们需要进一步确定到底哪块出问题，而不是笼统地回答。

因此，算法的应用场景也比较清楚，该场景满足以下三个条件:

• 场景具有多个流程。类似于我们求的是多项式计算入 (1+2*4 - 7) / 3，而不是只有一个流程，如 1 + 3。
• 场景中每个流程都可以量化，即使用 KPI 表示健康情况。
• 场景中各个流程中具有一定的相关性。如果每个流程都相互独立，那就不存在寻找 root cause 的需求了。比如三个相互独立的房间中有三个人，哪个房间的灯亮了一定就是那个房间的人干的事情，不需要一个一个步骤调查分析了。

20.1.2 论文提出了什么算法，是如何找到 root cause ?

论文用到的最核心的算法应当包括：

• 蒙特卡罗搜索树 Monte Carlo tree search (MCTS)，用来搜索定位异常发生地。
• Potential Score (ps) 用来评估每个元素的潜在风险程度的方法。

关于这两个方法如何应用在论文中在后面做详细介绍，目前给一个粗略的答复。

1. 论文通过 Potential Score 评估每个结点的异常程度；
2. 论文通过 Monte Carlo Tree Search 定位异常根因。

20.1.3 总体概述论文内容

论文提出了采用 MCTS 方法 的 HotSpot 框架（在异常定位文献中首次出现），可以捕捉异常是如何从根本原因在整个聚合层次结构中传播的（确定异常根因），并且论文提出了一种分层剪枝的方法来进一步缩小搜索空间以节省搜索时间，提高算法速率。

20.2 相关技术背景介绍

20.2.1 additive KPI

比如 page view, revenue, traffic volume，大概可以理解为数值类型的。事实上后来的很多KPI异常检测论文默认数据对象就是数值类型的。

20.2.2 多特征 additive KPI 数据的异常定位

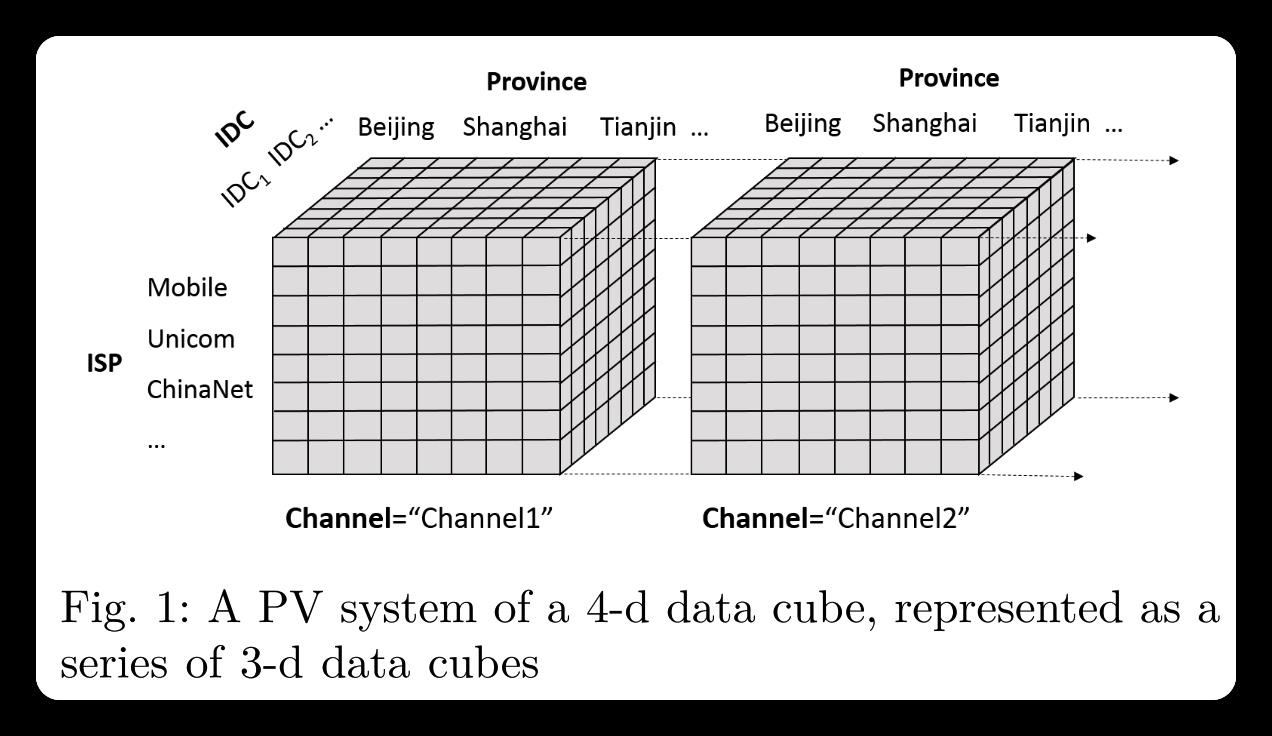
多特征additive KPI 异常定位问题是识别最有可能导致总 KPI 值异常变化的模块及其元素。论文原文使用的是长方体（cuboid）来表示模块的概念，如图一所示：

20.2.3 Monte Carlo Tree Search（MCTS）蒙特卡罗搜索

蒙特卡洛树搜索（MCTS）是一种启发式搜索算法，适用于某些类型的决策过程，尤其是游戏中使用的决策过程（例如AlphaGo）。

这部分的资料比较多，感兴趣的可以自行搜索，可以参考一下 https://blog.csdn.net/qq_24178985/article/details/121803376。

不过也可以不急着深入理解这个方法，继续看其他部分。

20.3 论文阅读

这里跳几个比较重要的部分进行介绍

20.3.1 Contribution

• 为了处理根源的巨大搜索空间，HotSpot 采用了 MCTS 方法（文献中首次应用在异常定位）。
• 在采用 MCTS 中的动作值是我们基于“涟漪效应（ripple effect）”的新颖的潜在得分（potential score），其捕获了对于多维 additive KPI，一个属性组合的KPI值的改变（作为原因）如何能够引起其他属性组合的KPI值改变（作为结果）。
• 我们提出了一种分层剪枝方法（在精神上类似于 Apriori 原理）来进一步减少搜索空间。
• 我们使用一个顶级全球搜索引擎的真实世界数据，表明 HotSpot 在有效性和鲁棒性方面都比现有的两种方法有了很大的改进，HotSpot对所有类型的案例的95%实现了超过90%的F-score，而对于现有方法，所有类型的案例中只有不到15%具有超过90%的F-score。
• 我们的实践经验表明，HotSpot 可以将手动工作的本地化时间从 1 小时以上缩短到 20秒以内。

20.3.2 问题定义

此部分描述了论文解决的是一个什么样的问题，先从定义出发：

这里是指接下来的论文、实验中可能用到的条目（term）的介绍说明，在公式中也会用到，这里我们详细介绍一下：

条目	定义	标识	举例
属性	每条PV记录的信息类别	-	$\text{Province (P), ISP(I), DC(D), Channel(C)}$
属性值	每个属性的候选值	-	$\text{Beijing, Shanghai, Guangdong for Province(P)}$
元素	每个属性的不同值的组合向量	$e=(p,i,d,c)$	$\text{(Beijing,*,*,*), (*,Mobile,*,*), (Beijing, Mobile,*,*)}$
PV值	根据元素的访问日志数	$v(e_i)$	$v(\text{Beijing,*,*,*})$
数据立方体	多维数据的数据结构	$n-dcube$	维度为P，I，D，C的四维数据立方体
长方体Cuboids	长方体是一个数据立方体，其维度在所有给定维度的子集中	$B_i$	$B_P,B_{P,I},B_{P,I,D},...$ for the 4-d data cube with the dimensions $\text{P, I, D, C}$
潜在得分Potential Score	衡量一组元素成为根本原因的潜力的概念	$ps$	$ps(S)$，$S=\text{(Beijing, *, *, *), (*, Mobile, *, *)}$

下面的两个表用来表示 PV 例子，网站上的PV记录可以有几个属性。 例如，“10:00:01（时间戳）； 北京、移动、DC1、Channel1“为记录，北京、移动、DC1、Channel1分别根据地区§、ISP(I)、数据中心(D)和频道©四个属性为候选值，其中$P=p$、$I=i$、$D=d$、$C=c$ 分别为地区、ISP、数据中心和 ADS 频道的36、10、6、10个不同值的集合。 $P$ 和 $I$ 的值基于客户端 IP，并分别使用 IP 到地理定位数据库和 BGP 表进行解析。 每个地区的 ISP 都是一个独立的公司，因此相同的 ISP 名称在不同的地区往往表现不同。 渠道是不同广告市场的标签，如医疗或教育。 表2 显示了PV记录的一些示例。

不同属性值组合的向量在本文中称为元素（element），表示为 $e=(p,i,d,c)$，其中 $p\in P$ 或者 $p=\ast$, $i\in I$ 或者 $i=\ast$, $d\in D$ 或者 $d=\ast$, $c\in C$ 或者 $c=\ast$, 这里的 $\ast$ 是通配符，当$e=(p,i,d,c)$在每一个时间尺度（如本文中的尺度为每分钟）中，我们根据一个元素 $e$ 来计算 PV 记录的数目，并将这个数字称为该元素的 PV 值，用 $v(e)$ 表示，即 $v(e)=$ 在特定时间尺度上的#个记录。 表3 显示了与表2中的PV记录相对应的PV值。

所有这些最细粒度元素的集合，如表3 中的元素，用叶子表示： $\text{LEAF}=e|e=(p,i,d,c),p\ne \ast ,i\ne \ast ,d\ne \ast ,c\ne \ast$。当一个或多个属性值为 * 时，其他元素都可以基于 Leaf 中的元素求和。例如，对于表 3 中 10:00（从10:00:00到10:00:59) 的三个元素，我们可以获得更粗粒度元素的值，例如：

$$\begin{array}{c}v\left(\text{ Beijing, Mobile, }D{C}_1,\ast \right)=2+1=3,\\ v(\text{ Bei jing },\ast ,\ast ,\ast )=2+1+3=6.\end{array}$$

根据聚集程度的不同，我们将元素划分为不同的集合，每个集合对应一个长方体。 长方体是数据立方体的子立方体，数据立方体是一种数据结构，允许在多维度上建模和查看数据[3]，例如，叶的元素构成一个4-D数据立方体，如图所示 1. 长方体表示为 $B_i$（ $i$ 可以是 $P$、$I$、$D$ 和 $C$ 中的任意组合），例如，$B_P$ 是一维长方体，$B_{P,I,D}$ 是三维长方体。 长方体的元素集 $B_i$ 用 $E(B_i)$ 来表示，比如， E ( B P ) = e ∣ e = ( p , ∗ , ∗ , ∗ ) , p ≠ ∗ E\\left(B_P\\right)=\\e \\mid e=(p, *, *, *), p \\neq *\\ E(B以上是关于《异常检测——从经典算法到深度学习》20 HotSpot：多维特征 Additive KPI 的异常定位的主要内容，如果未能解决你的问题，请参考以下文章

《异常检测——从经典算法到深度学习》20 HotSpot：多维特征 Additive KPI 的异常定位

异常检测——从经典算法到深度学习》14 对于流数据基于 RRCF 的异常检测

《异常检测——从经典算法到深度学习》16 基于VAE和LOF的无监督KPI异常检测算法

异常检测——从经典算法到深度学习》14 对于流数据基于 RRCF 的异常检测

异常检测——从经典算法到深度学习》14 对于流数据基于 RRCF 的异常检测

《异常检测——从经典算法到深度学习》15 通过无监督和主动学习进行实用的白盒异常检测