记录一些有点难（指我不会写的）的dp

Posted 2022-12-14 KaaaterinaX

HDU3236 Gift Hunting
好神奇，一开始以为是标记两个背包的状态，结果发现根本没法处理某个物品放在了哪个背包里。。

还没写完，稍微想一下思路大概就是先处理必须选择的物品，然后标记选完所有必选物品能达到的所有状态，再根据这些状态对非必选的物品进行状态转移。
给出状态分析思路： 代码t掉了，找个爹来帮我改改😅？

const int maxn=350;
const int maxm=505;

int p1[maxn],h1[maxn];
int p0[maxn],h0[maxn];
//记录所有必须买的物品买完了之后能到达的状态，然后可买可不买的物品从这些状态开始转移
int now[maxm][maxm][2];//滚动数组dp[v1][v2][0/1]=最大价值，记录当前用了v1/v2中的体积，以及是否使用免费的卷
int last[maxm][maxm][2];
bool vis[maxn][maxn][2];//记录把必须买的物品全买了之后达到的所有状态

———————————————————————————————————
CF688E The Values You Can Make
相当于两个维度的01背包（个人抽象理解），状态分析很巧妙。

const int maxn=507;
bool dp[maxn][maxn];//dp[i][j]=0/1，表示当前硬币总价值为i，这些硬币能否凑成j
int a[maxn];
int main()
    int n,K;
    cin>>n>>K;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    
    dp[0][0]=1;
    for(int k=1;k<=n;k++)
        for(int i=K;i>=0;i--)
            for(int j=K;j>=0;j--)
                if(dp[i][j]==1)
                    if(i+a[k]<=K)
                        dp[i+a[k]][j]=1;
                        dp[i+a[k]][j+a[k]]=1;
                    
                
            
        
    
    int ans=0;
    for(int i=0;i<=K;i++)
        if(dp[K][i]==1)
            ans++;
        
    
    cout<<ans<<endl;
    for(int i=0;i<=K;i++)
        if(dp[K][i]==1)
            cout<<i<<' ';
        
    
    cout<<endl;

———————————————————————————————————

CF82D Two out of Three

如何选择状态，才能让操作不具有后效性？

通过观察得出，在第$i$次收银的时候，可以选择的人只有$k，i\ast 2，i\ast 2+1，k$为上一次选择剩下的那个人。
那么每次选择只需要记录剩下了谁，因为只有这个会对后续选择产生影响。

这样一来状态转移方程就很好设了！

PS:这个题记忆化搜索部分我不会写。。把第一个答案写出来我已经尽力了TT。
（我晚点回来补上qaq）

//好了。。爷写了能算出第一个答案的代码了，接下来要进行记忆化搜索，记录状态是如何转移的。。。


const int maxn=1e3+100;//允许往后越界？

int a[maxn];//每个人的权值

int dp[maxn][maxn];//dp[i][j]=选了i次，剩下j号人的最小花费

int pr[maxn][maxn][3];//记忆化数组

int main()
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>a[i];
    
    memset(dp,INF,sizeof(dp));
    
    dp[1][3]=max(a[1],a[2]);
    dp[1][2]=max(a[1],a[3]);
    dp[1][1]=max(a[2],a[3]);
    
    for(int i=2;i<=(n>>1)+1;i++)
        //第i次选择
        //对每个可选择剩下的元素进行枚举
        for(int j=1;j<=i*2+1;j++)
            if(j==i*2+1)
                //这种情况可以由上一次所有的状态转移而来
                int minn=INF;
                for(int k=1;k<=(i-1)*2+1;k++)
                    minn=min(minn,dp[i-1][k]+max(a[k],a[i*2]));
                
                dp[i][j]=minn;
            
            else if(j==i*2)
                int minn=INF;
                for(int k=1;k<=(i-1)*2+1;k++)
                    minn=min(minn,dp[i-1][k]+max(a[k],a[i*2+1]));
                
                dp[i][j]=minn;
            
            else
                dp[i][j]=dp[i-1][j]+max(a[i*2],a[i*2+1]);
            
        
    
//    for(int i=1;i<=n/2+1;i++)
//        cout<<"i="<<i<<endl;
//        for(int j=1;j<=i*2+1;j++)
//            cout<<"j="<<j<<endl;
//            cout<<"dp="<<dp[i][j]<<endl;
//        
//        cout<<endl;
//    
    cout<<dp[(n>>1)+1][n+1]<<endl;

———————————————————————————————————
Max Sum Plus Plus
牛马题目，看了好久好久好久好久好久好久。。hatui

n的范围非常大，所以必须压缩时间以及空间。用到了dp优化的常用手段：记录最大值避免重复遍历、滚动数组优化。

const int maxn=1e6+7;

ll a[maxn];

ll dp[maxn];//记录当前组选到i时的最大值
ll Max[maxn];//记录上一组的最大值，有效位置仅到j-1

int main()
    int m,n;
    while(scanf("%d%d",&m,&n)!=EOF)
        for(int i=1;i<=n;i++)
            scanf("%lld",&a[i]);
            dp[i]=0;
            Max[i]=0;
        
        
        ll x=0;
        //对于每一个数，可以选择留在当前区间（如果它的前一个数选了的话），或到下一个区间
        for(int i=1;i<=m;i++)
            //选到第m组
            x=-LINF;//找这个组当前的最大值
            for(int j=i;j<=n;j++)
                dp[j]=max(dp[j-1]+a[j],Max[j-1]+a[j]);//可以选择接上一个或者重新开一组
                //边界问题：如果当前j=i，那么dp[j-1]和Max[j-1]记录的都是上一组选到j-1的最大值
                Max[j-1]=x;//选这一组的时候不会再用到这个值了，所以更新为第i组选到j-1的最大值，而不再是i-1组了
                x=max(x,dp[j]);
            
        
        printf("%lld\\n",x);
    

———————————————————————————————————
凸多边形的划分（acwing1069非免费题库）

是个很巧妙的区间dp。如果看出结果呈区间分布，思路就豁然开朗了。

首先这个数据的范围很大，long long都存不下，所以要用快读/快写来输入/输出int_128。

举个例子，对于一个八边形，如图：

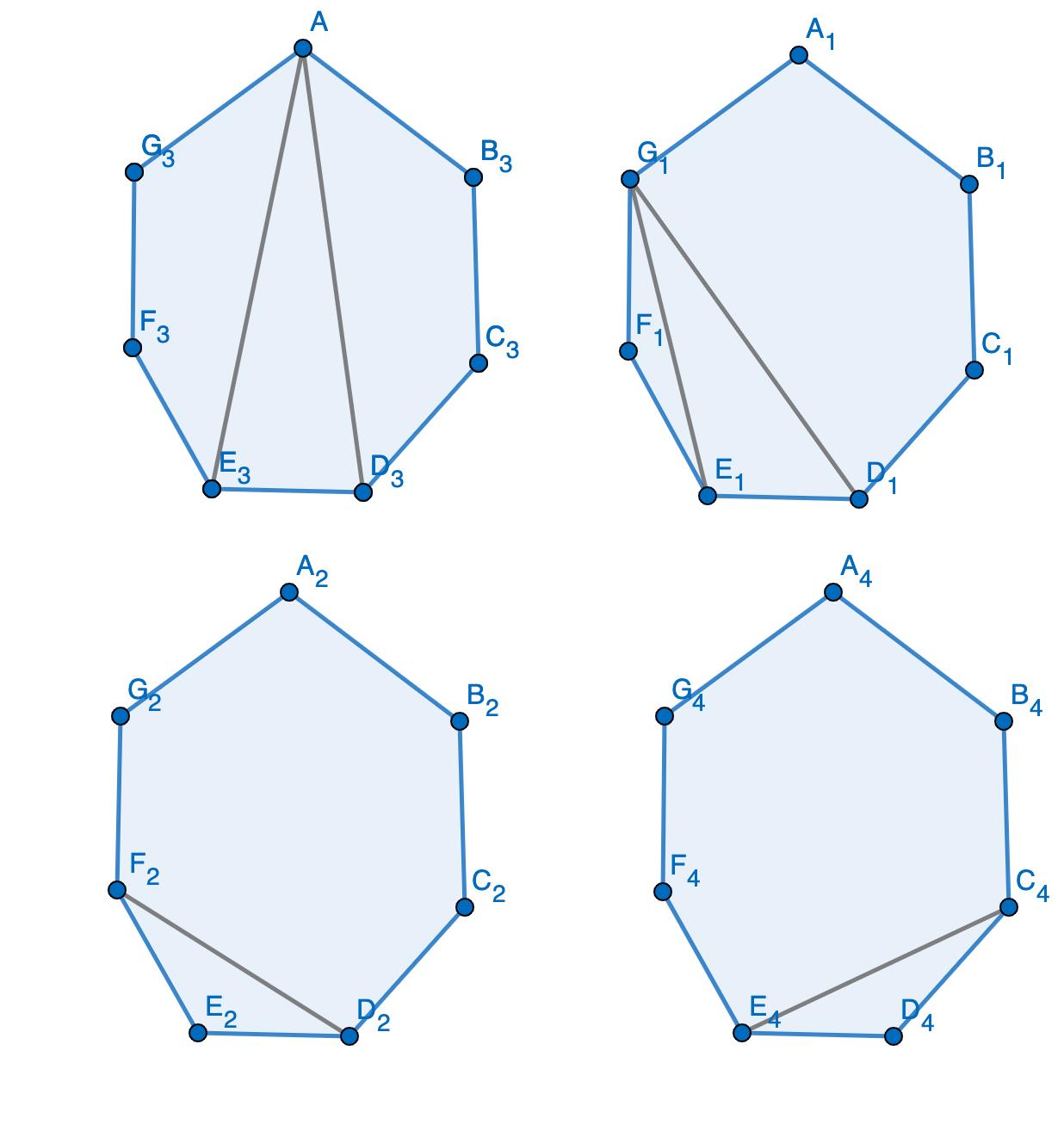
整个图形的划分可以由三段连续的区间合并而来，各区间的划分互不干扰。

从边界开始分析，可以得出状态转移方程。

__int128 a[105];

__int128 dp[105][105];

//环形区间dp？
//单起点枚举？
int main()
    int n;
    read(n);
    for(int i=1;i<=n;i++)
        read(a[i]);
        //a[i+n]=a[i];
    
    //最少都是三个节点一个区间
    //两个节点一个区间的可以直接默认为0
    for(int len=3;len<=n;len++)
        //枚举起点
        for(int i=1;i<=n-len+1;i++)
            int j=i+len-1;
            //枚举从哪转移
            dp[i][j]=1e30;
            for(int k=i+1;k<j;k++)
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[j]*a[k]);
            
        
    
    write(dp[1][n]);
    cout<<endl;

———————————————————————————————————
D. Coloring Brackets

前俩天这题过了，确实很有意思的一个题目。

有点水。。过几天重构一下。】】】】

const int maxn=710;
const int R=1;
const int B=2;
const int mod=1000000007;

string x;

ll dp[maxn][maxn][4][4];

int a[maxn];//记录匹配的括号

void match()
    //括号匹配
    stack<int> s;
    for(int i=0;i<x.size();i++)
        if(x[i]=='(')
            s.push(i);
        
        else
            a[s.top()]=i;
            a[i]=s.top();
            s.pop();
        
    


//这是一个神奇的区间dp，运用的是记忆化搜索的方法状态转移（）

ll DP(int l,int r,int lc,int rc)
    //lc和rc是传入外层的颜色
    ll res=0;
    if(l>=r) return 1;
    if(dp[l][r][lc][rc]!=-1) return dp[l][r][lc][rc];
    if(a[l]==r)
        //如果这个l r是匹配的
        if(lc!=B) res+=DP(l+1,r-1,B,0)%mod;
        if(lc!=R) res+=DP(l+1,r-1,R,0)%mod;
        if(rc!=B) res+=DP(l+1,r-1,0,B)%mod;
        if(rc!=R) res+=DP(l+1,r-1,0,R)%mod;
    else
        //如果不是匹配的，那么就继续分成更小的区间
        int m=a[l];
        if(lc!=R) res+=DP(l+1,m-1,R,0)*DP(m+1,r,0,rc)%mod;
        if(lc!=B) res+=DP(l+1,m-1,B,0)*DP(m+1,r,0,rc)%mod;
        res += (DP(l+1, m-1, 0, R) * DP(m+1, r, R, rc)) % mod;
        res += (DP(l+1, m-1, 0, B) * DP(m+1, r, B, rc)) % mod;
    
    dp[l][r][lc][rc]=res%mod;
    return res%mod;
    

int main()
    cin>>x;
    //跑一遍括号匹配,只需要记录每个字符匹配的字符在什么位置
    match();
    
    int n=(int)x.size();
    
    memset(dp,-1,sizeof dp);
    
    cout<<DP(0,n-1,0,0)<<endl;