算法设计一:分而治之
Posted Icedzzz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法设计一:分而治之相关的知识,希望对你有一定的参考价值。
分而治之解决问题思路:
- 分解原问题 :原问题分解成多个子问题
- 解决子问题 :递归地求解各个子问题
- 合并问题解 :将结果合并为原问题解
1. 归并排序
思路
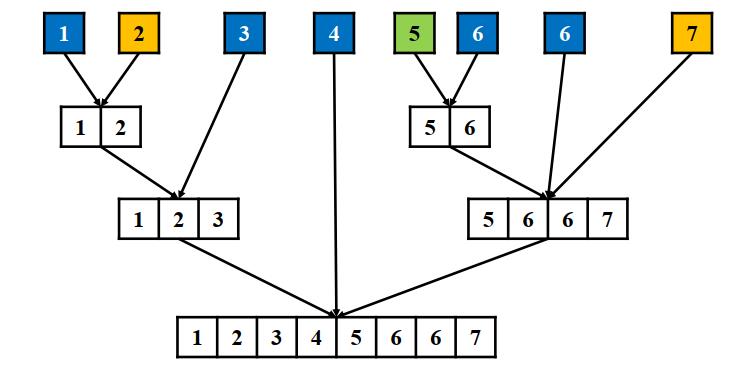
归并排序: 分解数组,递归求解,合并排序
-
分解原问题: 将数组A[1,n]分解成A[1,n/2]和A[n/2+1,n]子数组排序问题
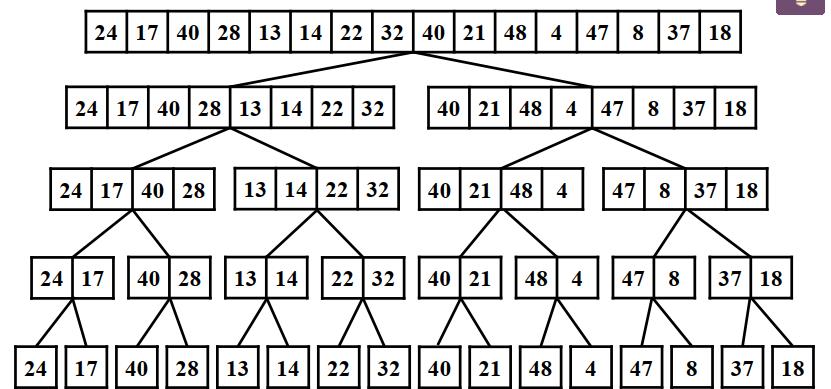
-
**解决子问题:**递归解决子问题得到有序的子数组
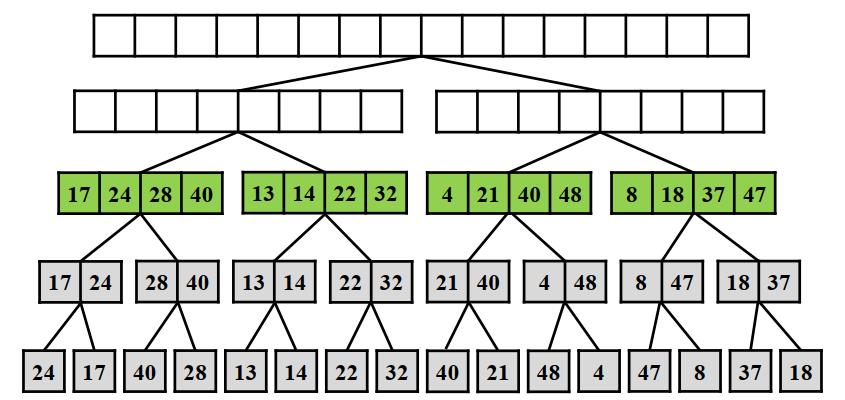
-
合并问题解:最后合并成有序的数组
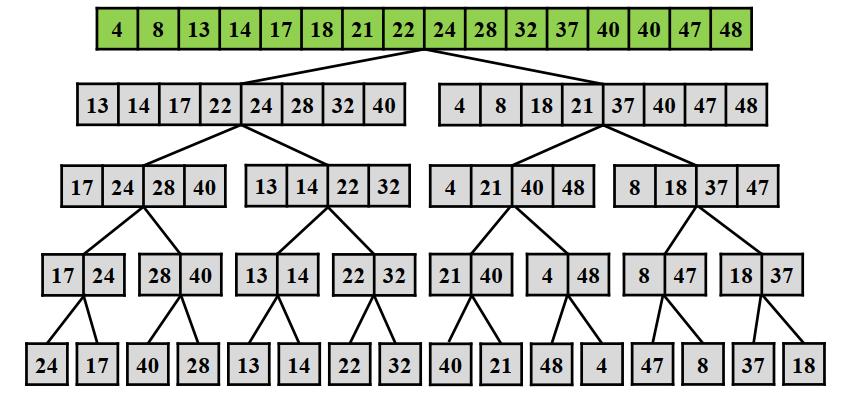
实现 伪代码+Java
伪代码:
 Java代码实现:
Java代码实现:
时间复杂度为𝑶(𝒏 𝐥𝐨𝐠 𝒏)
public static void MergeSort(int[] arr,int start, int end)
int middle=(end+start)>>2;
if (start<end)
MergeSort(arr,start,middle);
MergeSort(arr,middle+1,end);
Merge(arr,start,middle,end);
public static void Merge(int[] arr, int start, int middle, int end)
//创建临时数组存放排序好的数据
int[] temp = new int[end - start + 1];
int i=0;
int index1=0;
int index2=middle;
while (index1<middle&&index2<end)
if (arr[index1]>arr[index2])
temp[i]=arr[index2];
index2++;
else
temp[i]=arr[index1];
index1++;
i++;
//如果middle前数组已经遍历完
while (index2<end)
temp[i]=arr[index2];
index2++;
i++;
//如果middle后数组已经遍历完
while (index1<middle)
temp[i]=arr[index1];
index1++;
i++;
for (int j = 0; j < temp.length; j++)
arr[start+j]=temp[j];
2. 快速排序
归并排序特点是:简化分解,而侧重合并;而快速排序则相反:侧重分解,简化合并
快速排序基本思路:
- 选取固定位置主元x
- 维护两个部分(小于x和大于x两部分)的右端点i,j

- 考察数组元素arr[j],只与主元比较
- 如果arr[j]<=x,则交换arr[j]和arr[i+1]的位置,i和j右移
- 如果arr[j]>x,则j右移
- 把主元放在中间作为分界线(i+1)
- 左右数组按此方式递归划分数组
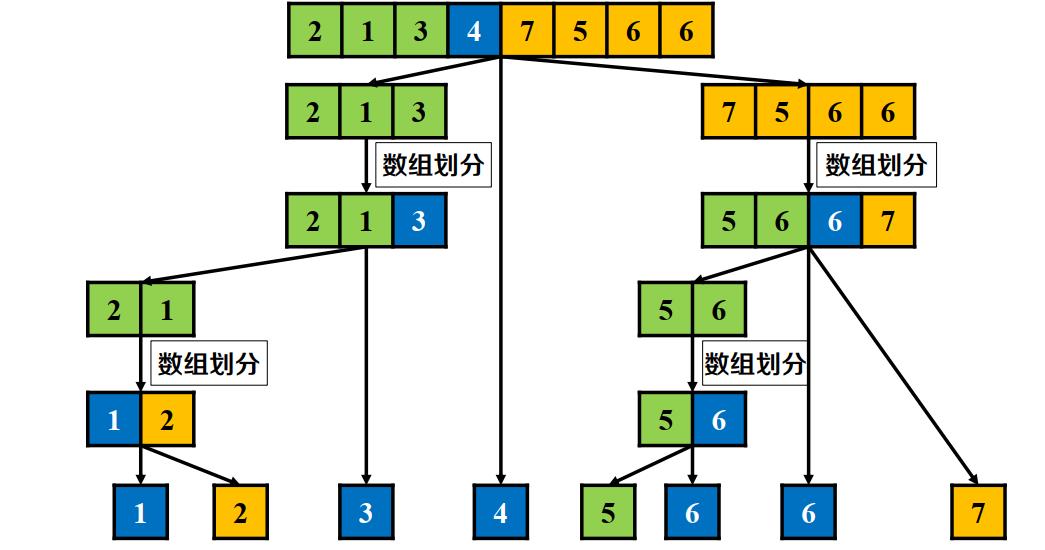
public static void QuickSortIndex(int[] arr,int start,int end)
if (start>end) return;
//选取主元,随机选取主元
Random random = new Random();
int X=arr[ random.nextInt(end-start)+start];
int temp;
temp=arr[end];
arr[end]=X;
arr[ random.nextInt(end-start)+start]=temp;
int i=start-1;
//如果arr[j]<=x 交换arr[j]和arr[i+1],j,i右移
//如果arr[j]>x,j右移
for (int j=start;j<=end-1;j++)
if (arr[j]<=X)
temp = arr[i + 1];
arr[i+1]=arr[j];
arr[j]=temp;
i++;
//最后将主元放在i+1位置上
temp=arr[i+1];
arr[i+1]=X;
arr[end]=temp;
QuickSort(arr,start,i);
QuickSort(arr,i+2,end);
注意点:
数组划分时如果选取固定位置主元,可以针对性构造最差情况,即每次分解主元均在数组中间时间复杂度为𝑶(𝒏 𝐥𝐨𝐠 𝒏),而每次分解后主元在数组两端时间复杂度为𝑶(𝒏𝟐)
解决方法:数组划分时选取随机位置主元,无法针对性构造最差情况,期望时间复杂度为𝑶(𝒏 𝐥𝐨𝐠 𝒏)
3. 最大子数组问题
方法一:暴力遍历,时间复杂度为𝑶(𝒏2)
/**
* 方法一:暴力求解
*/
public static int Method01(int[] arr)
int TempSum;
int MaxSum=0;
for (int i = 0; i < arr.length; i++)
TempSum=0;
for (int j=i;j<arr.length;j++)
TempSum+=arr[j];
if (TempSum>MaxSum)
MaxSum=TempSum;
return MaxSum;
方法二:优化暴力遍历中求和部分
第i到j数组的和等于第j个元素加上第i到j-1子数组和,减少重复计算 :S[i,j]=a[j]+S[i,j-1]
/**
* 优化求和的部分
* S[i,j]=a[j]+S[i,j-1]
*/
public static int Method02(int[] arr)
int TempSum;
int MaxSum=0;
for (int i = 0; i < arr.length; i++)
TempSum=0;
for (int j=i;j<arr.length;j++)
TempSum=TempSum+arr[j];
if (TempSum>MaxSum)
MaxSum=TempSum;
return MaxSum;
方法三:分治法
-
分解原问题: 最大子数组和问题可以拆分为三个部分:最大子数组位于左半数组、最大子数组位于右半数组和最大子数组横跨中点。
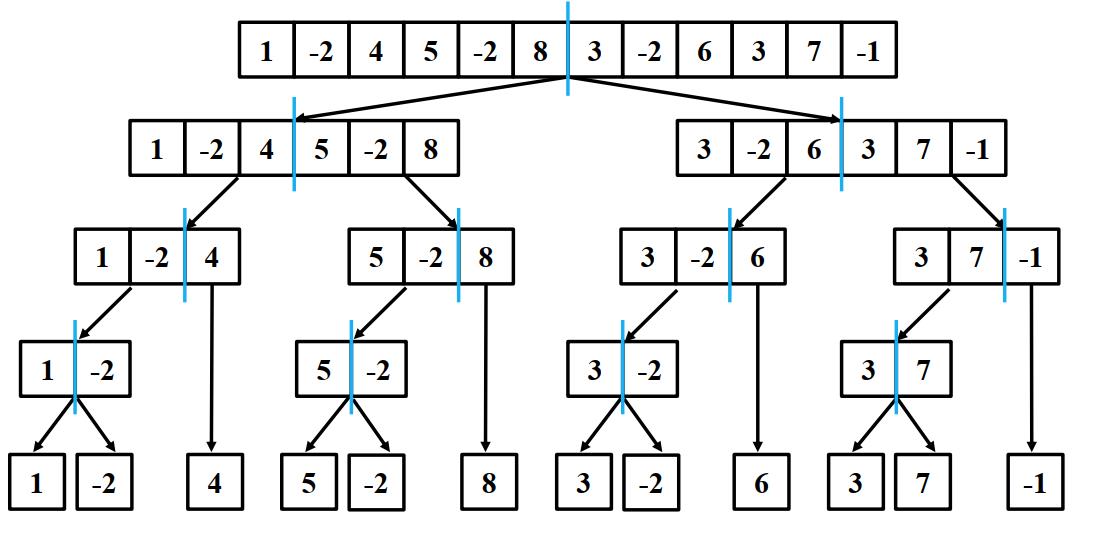
-
解决子问题: 分别求三个部分最大子数组
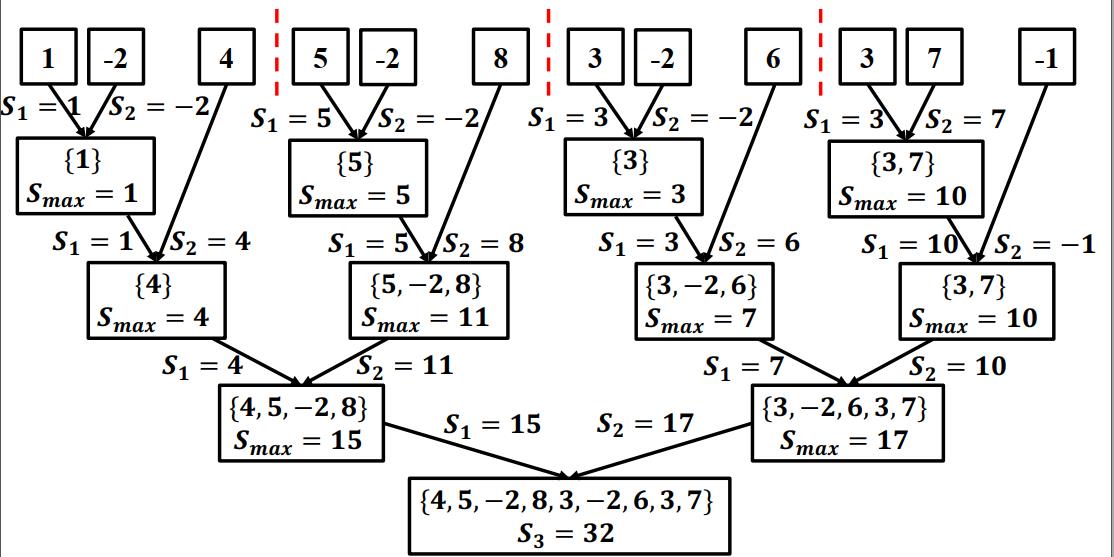
-
合并问题解: 三个部分最大子数组比较,取最大子数组
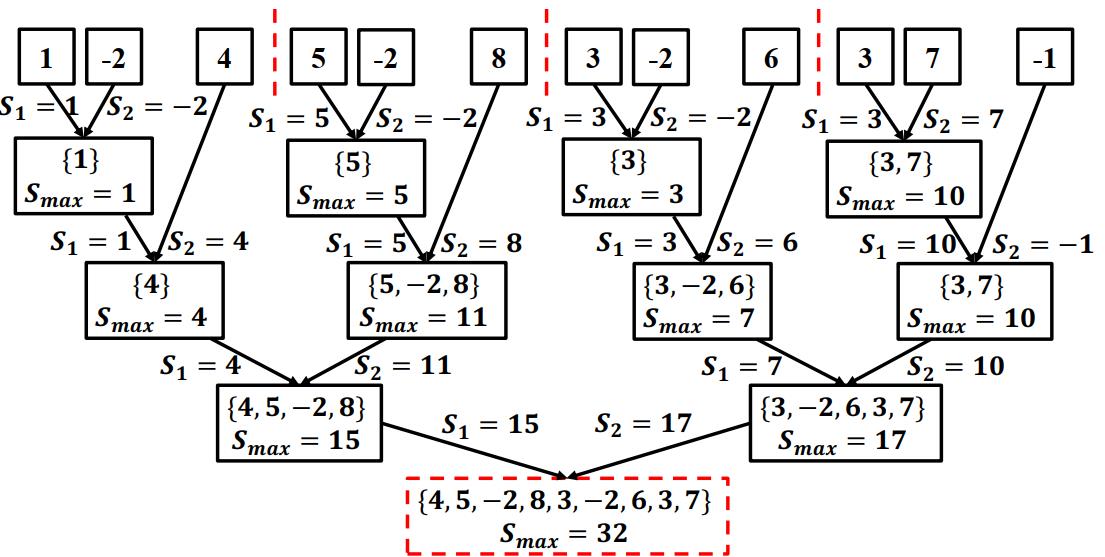
伪代码:
 Java实现: 时间复杂度:𝑶(𝒏𝐥𝐨𝐠 𝒏)
Java实现: 时间复杂度:𝑶(𝒏𝐥𝐨𝐠 𝒏)
/**
* 求左右两边最大子序列
* 再求从中间开始的最大子序列和
*/
public static int MaxSubArray(int[] arr,int low,int high)
if (low==high)
return arr[low];
else
int mid=(low+high)>>1;
int S1 = MaxSubArray(arr, low, mid);
int S2 = MaxSubArray(arr, mid + 1, high);
int S3 = CrossingSubArray(arr, low, mid, high);
return Math.max(Math.max(S1,S2),Math.max(S2,S3));
private static int CrossingSubArray(int[] arr, int low, int mid, int high)
int maxLeft=0;
int maxRight=0;
int SumL=0;
int SumR=0;
for (int i=mid;i>=low;i--)
SumL=SumL+arr[i];
if (SumL>maxLeft)
maxLeft=SumL;
for (int i=mid+1;i<=high;i++)
SumR=SumR+arr[i];
if (SumR>maxRight)
maxRight=SumR;
return maxLeft+maxRight;
4. 逆序对计数问题
求解数组中逆序对的个数,当𝒊 < 𝒋时𝑨 𝒊 > 𝑨 𝒋 的二元组(𝑨 𝒊 , 𝑨 𝒋 )
**方法一:**暴力求解𝑶(𝒏𝟐) 排除
方法二: 分而治之再直接计算𝑶(𝒏𝟐),排除
**方法三:**分而治之再排序求解𝑶(𝒏 𝒍𝒐𝒈𝟐𝒏)
**方法四:**分而治之:在归并排序的同时对逆序对进行计数𝑶(𝒏 𝒍𝒐𝒈 𝒏)
/**
* 分治法,利用归并排序,在每次排序时计算逆序数组个数
* 时间复杂度 O(n log N)
* @param arr
* @return
*/
public int InversePairMethod2(int[] arr)
if (arr == null || arr.length == 0)
return -1;
MegerSort(arr,0,arr.length-1);
return count;
int count=0;
/**
* 归并排序
*/
public int[] MegerSort(int[] arr, int start, int end)
if (start<end)
int middle=(end+start)/2;
MegerSort(arr,start,middle);
MegerSort(arr,middle+1,end);
Meger(arr,start,middle,end);
return arr;
private void Meger(int[] arr, int start, int middle, int end)
int[] temp=new int[end-start+1];
int index1=start;
int index2=middle+1;
int i=0;
while (index1<=middle&&index2<=end)
if (arr[index1]>arr[index2])
temp[i]=arr[index2];
count+=middle-index1+1;
index2++;
else
temp[i]=arr[index1];
index1++;
i++;
while (index1<=middle)
temp[i]=arr[index1];
i++;
index1++;
while(index2<=end)
temp[i]=arr[index2];
i++;
index2++;
for (int i1 = 0; i1 < temp.length; i1++)
arr[start+i1]=temp[i1];
5. 次序选择问题
给定数组𝑨 寻找其中第K小值
**方法一:**对数组先排序,再求第k小的元素𝑶(𝒏 𝐥𝐨𝐠 𝒏)
**方法二:**在快速排序过程中,查早第K小的元素
步骤:
-
选取固定位置主元,按快速排序方法进行切分数组,左边均小于主元,元素个数为𝒒 − 𝒑
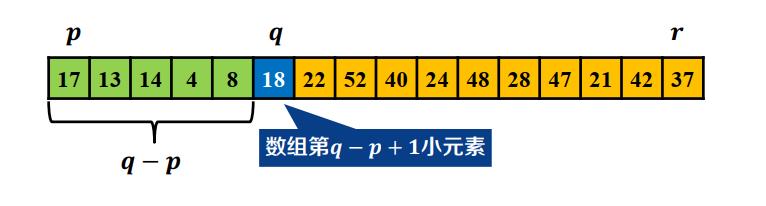
-
此时有三种情况:
- 𝒌 = 𝒒 − 𝒑 + 𝟏, 𝑨[𝒒]为数组第𝒌小元素
- 𝒌 < 𝒒 − 𝒑 + 𝟏, 数组第𝒌小元素在左边数组中
- 𝒌 > 𝒒 − 𝒑 + 𝟏, 在右边中寻找第𝒌 − (𝒒 − 𝒑 + 𝟏)小元素
-
如果是第二或者第三种情况,继续对左边或者右边进行快速排序
/**
* 次序选择
* @param arr
* @param start
* @param end
* @param k 元素次序
* @return
*/
public static int SelectionKMin(int[] arr,int start,int end,int k)
if (end<start) return start;
int x = 0;
//快速排序分区,返回主元位置
int q = QuickPartition(arr, start, end);
if (k==q-start+1)
x=arr[q];
else if (k<q-start+1)
x=SelectionKMin(arr,start,q,k);
else if (k>q-start+1)
x=SelectionKMin(arr,q+1,end,(k-(q-start+1)));
return x;
private static int QuickPartition(int[] arr, int start, int end)
int random = new Random().nextInt(end - start);
//随机定义主元,与最后一个值交换位置
int X=arr[random+start];
int temp;
arr[random+start]=arr[end];
arr[end]=X;
int i=start-1;
for (int j=start;j<=end-1;j++)
if (arr[j]<X)
temp = arr[j];
arr[j]=arr[i+1];
arr[i+1]=temp;
i++;
temp = arr[i + 1];
arr[i+1]=X;
arr[end]=temp;
return i+1;
注意: 与快速排序一样,次序选择过程中也有主元选择问题,最好情况复杂度为𝑶(𝒏),即第一次就选中了第k小的值,最坏情况𝑶(𝒏𝟐),每次均要选择最右边的主元,因此采用随机选取主元方法,期望时间复杂度为𝑶(𝒏)
以上是关于算法设计一:分而治之的主要内容,如果未能解决你的问题,请参考以下文章