python深度学习入门-感知机
Posted 诗雨时
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了python深度学习入门-感知机相关的知识,希望对你有一定的参考价值。
深度学习入门—感知机
博主微信公众号(左)、Python+智能大数据+AI学习交流群(右):欢迎关注和加群,大家一起学习交流,共同进步!


目录
摘要
- 感知机是具有输入和输出的算法。给定一个输入后,将输出一个既定的值。
- 感知机将权重和偏置设定为参数。
- 使用感知机可以表示与门和或门等逻辑电路。
- 异或门无法通过单层感知机来表示。
- 使用 2 层感知机可以表示异或门。
- 单层感知机只能表示线性空间,而多层感知机可以表示非线性空间。
- 多层感知机(在理论上)可以表示计算机。
1、感知机是什么
感知机(Perceptron):集语音、文字、手语、人脸、表情、唇读、头势、体势等多通道为一体的,并对这些通道的信息进行编码、压缩、集成、融合的计算机智能接口系统。
严格地讲,这里所说的感知机应该称为 “人工神经元” 或 “朴素感知机”,但是因为很多基本的处理是共通的,所以这里就简单地称为 “感知机”。
感知机接收多个输入信号,输出一个信号。
这里所说的 “信号” 可以想象成电流或河流那样具备 “流动性” 的东西。
像电流流过导线,向前方输送电子一样,感知机的信号也会形成流,向前方输送信息。
但是,和实际的电流不同的是,感知机的信号只有 “流 / 不流”(1/0)两种取值。
下图是一个接收两个输入信号的感知机的例子:
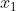 、
、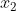 是输入信号,
是输入信号,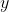 是输出信号,
是输出信号,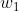 、
、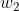 是权重(
是权重(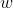 是 weight 的首字母)。
是 weight 的首字母)。
图中的 O 称为 “神经元” 或者 “节点”。
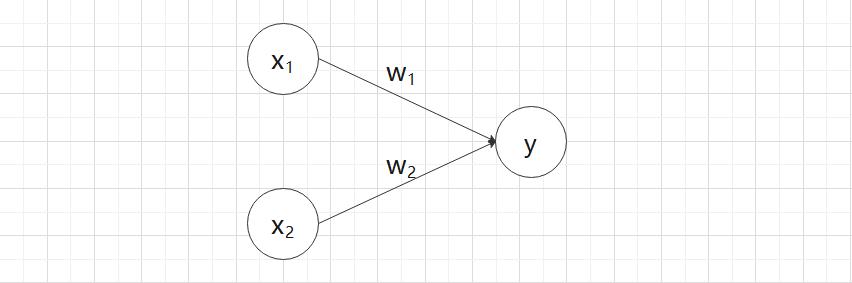
输入信号被送往神经元时,会被分别乘以固定的权重(

神经元会计算传送过来的信息的总和,只有当这个总和超过了某个界限值时,就会输出 1。这也称为 “神经元被激活”。这里将这个界限值称为阈值,用符号 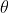 表示。
表示。
把上述内容用公式表示:
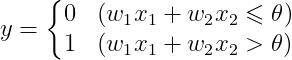
感知机的多个输入信号都有各自固有的权重,这些权重发挥着控制各个信号的重要性的作用。也就是说,权重越大,对应权重的信号的重要性就越高。
注:权重—指某一因素或指标相对于某一事物的重要程度,其不同于一般的比重,体现的不仅仅是某一因素或指标所占的百分比,强调的是因素或指标的相对重要程度,倾向于贡献度或重要性。
2、简单逻辑电路
2.1 与门(AND gate)
与门是有两个输入和一个输出的门电路。
与门真值表(输入信号和输出信号的对应表):与门仅在两个输入 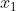 和
和 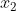 均为 1 时输出 1,其他时候则输出 0。
均为 1 时输出 1,其他时候则输出 0。

使用感知机来表示与门:我们需要做的就是确定能满足上图与门真值表的 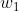 、
、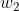 、
、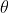 的值。
的值。
实际上满足上图与门真值表条件的参数选择方法有无数多个,以下都是满足上图与门真值表的条件参数:
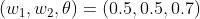
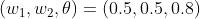
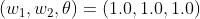
设定这样的参数后,仅当 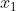 和
和 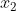 同时为 1 时,信号的加权总和才会超过给定的阈值
同时为 1 时,信号的加权总和才会超过给定的阈值 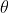 。
。
2.2 与非门(NAND gate)
NAND 是 Not AND 的意思,与非门就是颠倒了与门的输出。
与非门真值表(输入信号和输出信号的对应表):与非门仅在两个输入 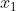 和
和 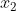 均为 1 时输出 0,其他时候则输出 1。
均为 1 时输出 0,其他时候则输出 1。

要表示与非门,可以用
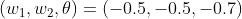
这样的组合(其他的组合也是无限存在的)。
实际上,只要把实现与门的参数值符号取反,就可以实现与非门。
2.3 或门(OR gate)
或门是 “只要有一个输入信号是 1,输出就为 1” 的逻辑电路。
或门真值表(输入信号和输出信号的对应表):或门在两个输入 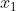 和
和 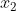 只要其中一个值为 1 时输出1,其他时候则输出 0。
只要其中一个值为 1 时输出1,其他时候则输出 0。
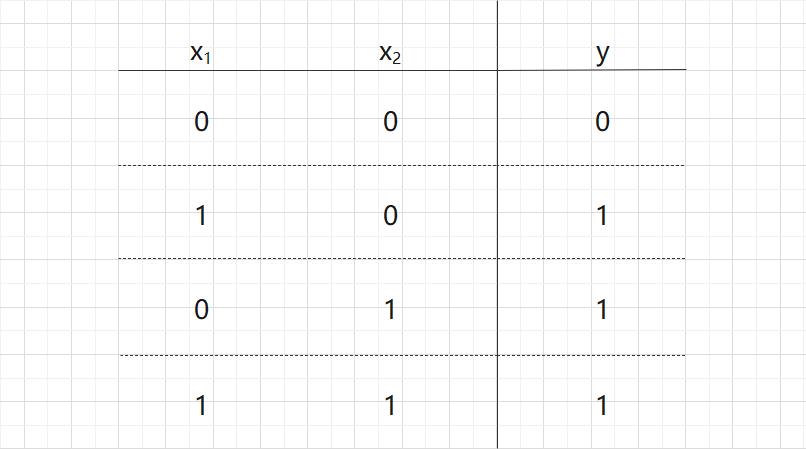
注:与门、与非门、或门 的感知机构造是一样的。实际上,3 个门电路只有参数的值(权重和阈值)不同。也就是说,相同构造的感知机,只需要通过适当地调整参数的值,就可以像 “变色龙演员” 表演不同的角色一样,变身为与门、与非门、或门。
3、感知机的实现
3.1 简单的实现(比较直接、容易理解)
(1)与门
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1(2)与非门
def NAND(x1, x2):
w1, w2, theta = -0.5, -0.5, -0.7
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
NAND(0, 0) # 输出1
NAND(1, 0) # 输出1
NAND(0, 1) # 输出1
NAND(1, 1) # 输出0(3)或门
def OR(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.2
tmp = x1 * w1 + x2 * w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
OR(0, 0) # 输出0
OR(1, 0) # 输出1
OR(0, 1) # 输出1
OR(1, 1) # 输出13.2 导入权重和偏置
将
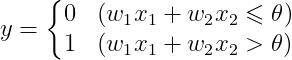
中的 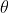 换成
换成 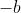 ,于是得到下面的公式来表示感知机行为:
,于是得到下面的公式来表示感知机行为:
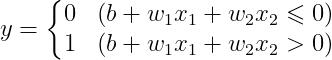
两个公式虽然有一个符号不同,但表达的内容是完全相同的。
此处,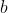 称为偏置,
称为偏置,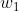 和
和 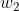 称为权重。
称为权重。
计算过程:计算输入信号和权重的乘积,然后加上偏置,如果这个值大于 0 则输出 1,否则输出 0。
3.3 使用权重和偏置的实现
权重 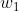 和
和 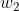 的作用:控制输入信号的重要性;
的作用:控制输入信号的重要性;
偏置 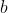 的作用:调整神经元被激活的容易程度(输出信号为 1 的程度)。
的作用:调整神经元被激活的容易程度(输出信号为 1 的程度)。
比如,若 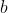 为 -0.1,则只要输入信号的加权总和超过 0.1,神经元就会被激活。但是如果
为 -0.1,则只要输入信号的加权总和超过 0.1,神经元就会被激活。但是如果 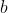 为 -20.0,则输入信号的加权总和必须超过20.0,神经元才会被激活。像这样,偏置的值决定了神经元被激活的容易程度。
为 -20.0,则输入信号的加权总和必须超过20.0,神经元才会被激活。像这样,偏置的值决定了神经元被激活的容易程度。
(1)与门
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2]) # 输入
w = np.array([0.5, 0.5]) # 权重
b = -0.7 # 偏置
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1(2)与非门
import numpy as np
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
NAND(0, 0) # 输出1
NAND(1, 0) # 输出1
NAND(0, 1) # 输出1
NAND(1, 1) # 输出0(3)或门
import numpy as np
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
OR(0, 0) # 输出0
OR(1, 0) # 输出1
OR(0, 1) # 输出1
OR(1, 1) # 输出14、感知机的局限性
4.1 异或门(XOR gate)
异或门也被称为逻辑异或电路。
异或门真值表(输入信号和输出信号的对应表):异或门仅在两个输入 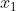 和
和 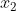 中的一方值为 1 时输出 1,其他时候则输出 0。
中的一方值为 1 时输出 1,其他时候则输出 0。
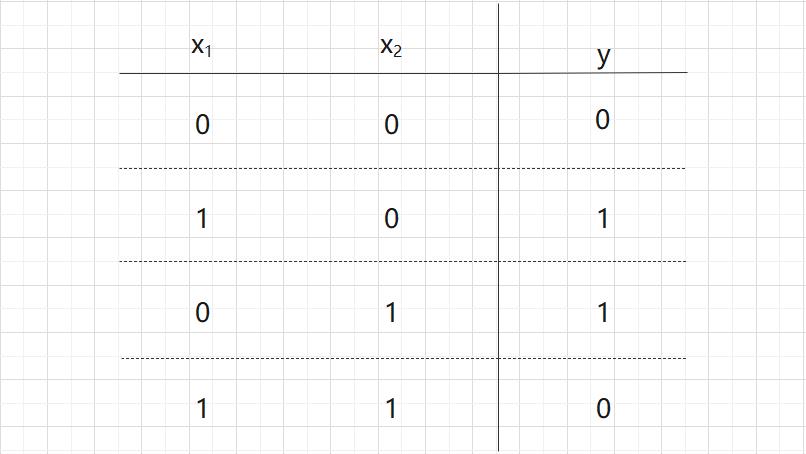
实际上,用前面介绍的感知机是无法实现这个异或门的。为什么用感知机可以实现与门、与非门、或门,却无法实现异或门呢?下面我们尝试通过画图来思考其中的原因。
首先,我们尝试着将或门的动作形象化。或门的情况下,当权重参数
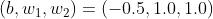
时,可满足上图的异或门真值表条件。此时,感知机可用下面的公式表示:
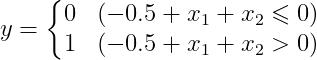
该公式表示的感知机会生成由直线 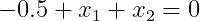 分隔开的两个空间,其中一个空间输出 1,另一个空间输出 0。
分隔开的两个空间,其中一个空间输出 1,另一个空间输出 0。
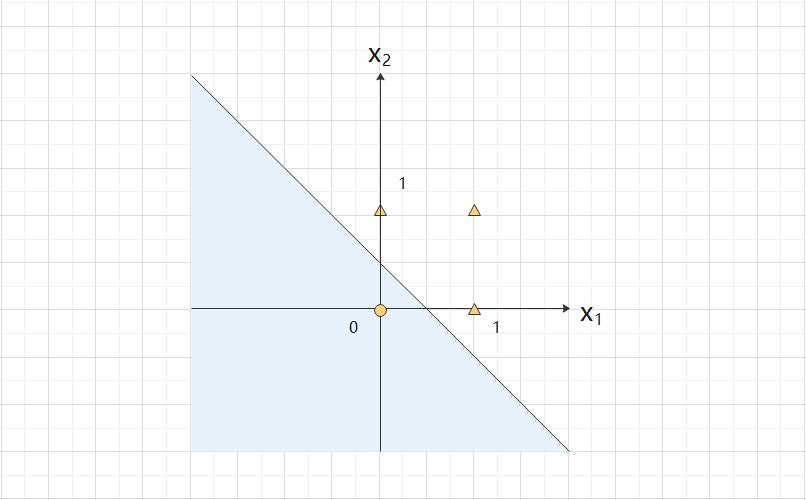
或门在 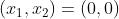 时输出 0,在
时输出 0,在 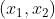 为 (0, 1)、(1, 0)、(1, 1) 时输出 1。
为 (0, 1)、(1, 0)、(1, 1) 时输出 1。
在上图中, 表示 0,
表示 0,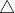 表示 1。如果想要制作或门,需要用直线将上图中的
表示 1。如果想要制作或门,需要用直线将上图中的  和
和  区分开。实际上,刚才的那条直线就将这 4 个点正确地分开了。
区分开。实际上,刚才的那条直线就将这 4 个点正确地分开了。
那么,换成异或门的话会如何呢?能否像或门那样,用一条直线做出分隔下图的  和
和  的空间呢?
的空间呢?
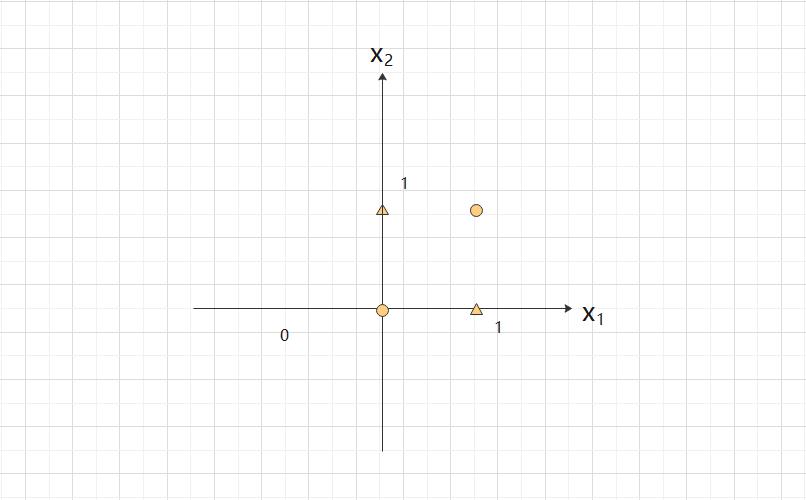
想要用一条直线将上图中的  和
和  分开,无论如何都做不到。事实上,用一条直线是无法将
分开,无论如何都做不到。事实上,用一条直线是无法将  和
和 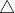 分开的。
分开的。
4.2 线性和非线性
上图中的  和
和  无法用一条直线分开,但是如果将 “直线” 这个限制条件去掉,就可以实现了。比如,我们可以想下图那样,作出分开
无法用一条直线分开,但是如果将 “直线” 这个限制条件去掉,就可以实现了。比如,我们可以想下图那样,作出分开  和
和  的空间。
的空间。
感知机的局限性就在于它只能表示由一条直线分隔的空间(单层感知机无法表示异或门 / 单层感知机无法分离非线性空间)。上图这样弯曲的曲线无法用感知机表示。
由上图这样的曲线分割而成的空间称为非线性空间,由直线分隔而成的空间称为线性空间。
线性、非线性这两个术语在机器学习领域很常见,可以将其想象成图 1-6 和 图 1-8 所示的直线和曲线。
5、多层感知机
感知机不能表示异或门让人们很遗憾,但也无需悲观。实际上,感知机的绝妙之处在于它可以 “层叠加”(通过层叠加来表示异或门)。
5.1 已有门电路的组合
异或门的制作方法有很多,其中之一就是组合我们前面做好的与门、与非门、或门 进行配置。这里,与门、与非门、或门用图 1-9 的符号表示。另外,图 1-9 中与非门前端的 O 表示反转输出的意思。
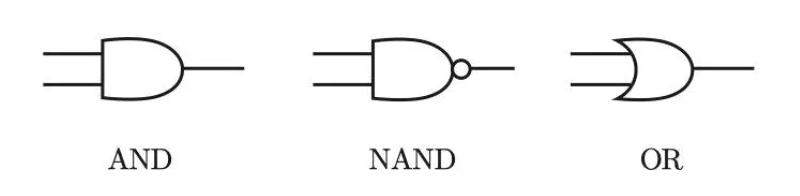
通过组合与门、与非门、或门实现异或门:
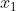 和
和 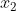 表示输入信号,
表示输入信号,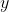 表示输出信号。
表示输出信号。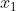 和
和 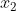 是与非门和或门的输入,而与非门和或门的输出则是与门的输入。
是与非门和或门的输入,而与非门和或门的输出则是与门的输入。
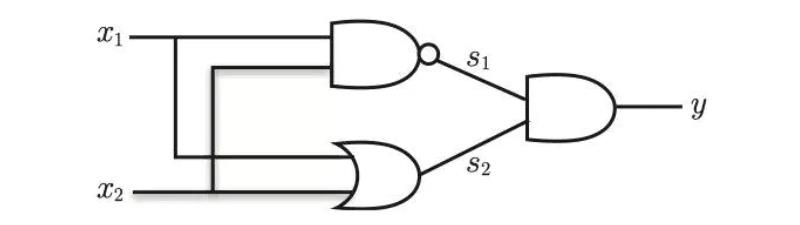
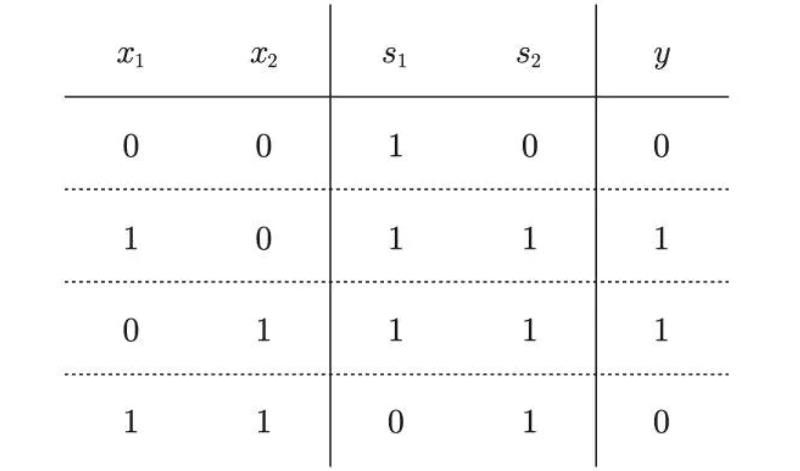
将 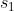 作为与非门的输出,将
作为与非门的输出,将 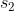 作为或门的输出,填入真值表中。结果如图 1-11 所示,观察
作为或门的输出,填入真值表中。结果如图 1-11 所示,观察 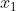 、
、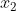 、
、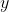 ,可以发现确实符合异或门的输出。
,可以发现确实符合异或门的输出。
5.2 异或门的实现
使用之前定义的 ADD 函数、NAND 函数、OR 函数,实现异或门:
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w * x) + b
if tmp <= 0:
return 0
else:
return 1
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
if __name__ == "__main__":
XOR(0, 0) # 输出0
XOR(1, 0) # 输出1
XOR(0, 1) # 输出1
XOR(1, 1) # 输出0使用感知机的表示方法(明确地显示神经元)来表示异或门:
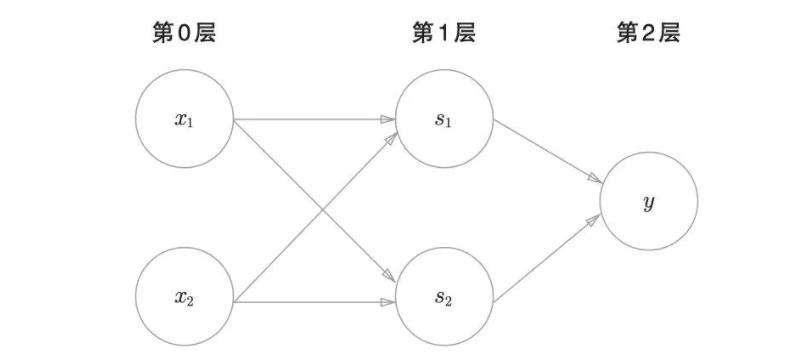
如图 2-12 所示,异或门是一种多层结构的神经网络。这里将最左边的一列称为第 0 层,中间的一列称为第 1 层,最右边的一列称为第 2 层。
与门、与非门、或门是单层感知机,而异或门是 2 层感知机。叠加了多层的感知机也称为多层感知机(nulti-layered perceptron)。
信号传递过程:
(1)第 0 层的两个神经元接收输入信号,并将信号发送至第 1 层的神经元;
(2)第 1 层的神经元将信号发送至第 2 层的神经元,第 2 层的神经元输出 y。
以上是关于python深度学习入门-感知机的主要内容,如果未能解决你的问题,请参考以下文章