java二叉树的实现

Posted 2022-12-11 加冰雪碧

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了java二叉树的实现相关的知识，希望对你有一定的参考价值。

java二叉树的实现

树在编程问题中有着很广泛的应用，而二叉树又是其中出现频次较高的一种（可以很方便的将普通的树转化为二叉树）。本文从无到有的实现了二叉树，如果对树的基础概念不太了解可以先看一下概念。

接口的抽取

公共树接口 TreeInterface

package com.fsc.mytree;

/**
 * 所有树共有的公共接口
 * @author fsc
 *
 * @param <T>
 */
public interface TreeInterface<T> 
	/**
	 * 返回根节点中的数据域
	 * @return
	 */
	public T getRootData();
	
	/**
	 * 返回数的高度
	 * @return
	 */
	public int getHeight();
	
	/**
	 * 返回节点的数目
	 * @return
	 */
	public int getNumberOfNodes();
	
	/**
	 * 判断树是否为空
	 * @return
	 */
	public boolean isEmpty();
	
	/**
	 * 清空树
	 */
	public void clear();

插入和删除的操作因为和具体的树相关，所以在基本的接口中并没有声明他们。而对树的各种顺序遍历又不是每个树的应用都会用到（很可能只是用数据结构来进行存储而不需要展示），所以下面将抽取出一个专门的接口用于声明各种顺序遍历。

树的遍历接口 TreeIteratorInterface

package com.fsc.mytree;

import java.util.Iterator;

/**
 * 树遍历器的接口，根据需要返回遍历器实例
 * 
 * @author fsc
 * 
 * @param <T>
 */
public interface TreeIteratorInterface<T> 
	/**
	 * 得到前序遍历的遍历器
	 * @return
	 */
	public Iterator<T> getPreorderIterator();
	/**
	 * 得到后序遍历的遍历器
	 * @return
	 */
	public Iterator<T> getPostorderIterator();
	/**
	 * 得到中序遍历的遍历器
	 * @return
	 */
	public Iterator<T> getInorderIterator();
	/**
	 * 得到层序遍历的遍历器
	 * @return
	 */
	public Iterator<T> getLevelorderIterator();

二叉树接口 BinaryTreeInterface

package com.fsc.mytree;

public interface BinaryTreeInterface<T> extends TreeInterface<T>, TreeIteratorInterface<T> 
	/**
	 * 创建出一个以rootData为根节点的树（没有左右子树）
	 * @param rootData
	 */
	public void setTree(T rootData);
	/**
	 * 创建一个以rootData为根节点的树
	 * @param rootData
	 * @param leftTree 左子树
	 * @param rightTree 右子树
	 */
	public void setTree(T rootData, BinaryTreeInterface<T> leftTree, BinaryTreeInterface<T> rightTree);

因为很大一部分的使用中没有用到获得左右子树的功能，所以这里没有定义获取子树的方法，如果对此方法有需要可自行定义。

代码实现

二叉树节点 BinaryNode

在之前写过的链表的实现中提到了内部节点Node，用来存储节点的内部数据和维护下一节点的引用。在对树进行实现的过程中同样需要引入节点Node。与链表的实现不同，TreeNode的实现相对来说复杂一些，所以没有将其作为二叉树实现类的内部类，避免在一个类中代码过多。

package com.fsc.mytree;

class BinaryNode<T> 
	/*** 节点内部数据域*/
	private T data;
	/*** 左孩子的引用*/
	private BinaryNode<T> left;
	/*** 右孩子的引用*/
	private BinaryNode<T> right;

	public BinaryNode(T data) 
		this(data, null, null);
	

	public BinaryNode(T data, BinaryNode<T> left, BinaryNode<T> right) 
		this.data = data;
		this.left = left;
		this.right = right;
	

	public T getData() 
		return data;
	

	public BinaryNode<T> getLeftChild() 
		return left;
	

	public BinaryNode<T> getRightChild() 
		return right;
	

	public boolean hasLeftChild() 
		return left != null;
	

	public boolean hasRightChild() 
		return right != null;
	
        <pre name="code" class="java">        /*** 当前节点是否为叶子节点*/
	public boolean isLeaf() 
		return (left == null) && (right == null);
	

	public void setData(T newData) 
		data = newData;
	

	public void setLeftChild(BinaryNode<T> leftChild) 
		left = leftChild;
	

	public void setRightChild(BinaryNode<T> rightChild) 
		right = rightChild;
	

	/**
	 * 将以当前节点为根的二叉树进行赋值，并将复制后的根节点返回
	 * @return
	 */
	public BinaryNode<T> copy() 
		BinaryNode<T> newRoot = new BinaryNode<T>(data);
		if(left != null)
			newRoot.setLeftChild(left.copy());
		
		if(right != null)
			newRoot.setRightChild(right.copy());
		
		return newRoot;
	

	/**
	 * 以当前节点为根的树的高度
	 * @return
	 */
	public int getHeight() 
		return getHeight(this);
	
	
	private int getHeight(BinaryNode<T> node)
		int height = 0;
		if(node != null)
			height = 1 +Math.max(getHeight(node.left), getHeight(node.right));
		
		return height;
	

	/**
	 * 以当前节点为根的树的节点数
	 * @return
	 */
	public int getNumberOfNode() 
		return getNumberOfNode(this);
	
	
	private int getNumberOfNode(BinaryNode<T> node)
		int leftNum = 0;
		int rightNum= 0;
		
		if(node.left != null)
			leftNum = getNumberOfNode(node.left);
		
		if(node.right != null)
			rightNum = getNumberOfNode(node.right);
		
		return leftNum + rightNum + 1;

二叉树除了初始化和遍历外基本上所有的操作都是委托给节点类来进行处理，所以在节点类里也就相应的实现了对树的复制，求树高以及求树的所有节点数等方法。

上述代码没有很难理解的地方，需要注意的是在复制树时copy()方法对节点进行了递归的调用。在求树高和节点数时同样进行了递归的调用，不过都将具体实现方法设为私有，屏蔽了外界的访问。

二叉树实现 BinaryTree

package com.fsc.mytree;

import java.util.Iterator;

public class BinaryTree<T> implements BinaryTreeInterface<T> 
	/*** 持有树根节点*/
	public BinaryNode<T> root;

	public BinaryTree() 
		root = null;
	

	public BinaryTree(T rootData) 
		root = new BinaryNode<T>(rootData);
	

	public BinaryTree(T rootData, BinaryTree<T> leftTree,
			BinaryTree<T> rightTree) 
		//调用私有方法对树进行构建
		privateSetTree(rootData, leftTree, rightTree);
	

	@Override
	public void setTree(T rootData) 
		root = new BinaryNode<T>(rootData);
	

	@SuppressWarnings("unchecked")
	@Override
	public void setTree(T rootData, BinaryTreeInterface<T> leftTree,
			BinaryTreeInterface<T> rightTree) 
		privateSetTree(rootData, (BinaryTree<T>)leftTree, (BinaryTree<T>)rightTree);
	
	
	private void privateSetTree(T rootData, BinaryTree<T> leftTree,
			BinaryTree<T> rightTree) 
		// TODO Auto-generated method stub
	

	@Override
	public void clear() 
		root = null;
	

	@Override
	public int getHeight() 
		return root.getHeight();
	

	@Override
	public int getNumberOfNodes() 
		return root.getNumberOfNode();
	

	@Override
	public T getRootData() 
		if(root != null)
			return root.getData();
		
		return null;
	

	@Override
	public boolean isEmpty() 
		return root == null;
	
	

	public void setRootData(T rootData)
		root.setData(rootData);
	
	public void setRootNode(BinaryNode<T> rootNode)
		root = rootNode;
	
	public BinaryNode<T> getRootNode()
		return root;
	
	

	/**
	 * 简单的前序遍历（仅打印）
	 */
	public void preorderTraverse()
		preorderTraverse(root);
	
	private void preorderTraverse(BinaryNode<T> node)
		if(node != null)
			System.out.println(node.getData());
			preorderTraverse(node.getLeftChild());
			preorderTraverse(node.getRightChild());
		
	
	
	
	/**
	 * 简单的中序遍历（仅打印）
	 */
	public void inorderTraverse()
		inorderTraverse(root);
	
	private void inorderTraverse(BinaryNode<T> node)
		if(node != null)
			inorderTraverse(node.getLeftChild());
			System.out.println(node.getData());
			inorderTraverse(node.getRightChild());
		
	
	
	/**
	 * 简单的后序遍历（仅打印）
	 */
	public void postorderTraverse()
		postorderTraverse(root);
	
	private void postorderTraverse(BinaryNode<T> node)
		if(node != null)
			postorderTraverse(node.getLeftChild());
			postorderTraverse(node.getRightChild());
			System.out.println(node.getData());
		
	
	
	
	@Override
	public Iterator<T> getInorderIterator() 
		// TODO Auto-generated method stub
		return null;
	

	@Override
	public Iterator<T> getLevelorderIterator() 
		// TODO Auto-generated method stub
		return null;
	

	@Override
	public Iterator<T> getPostorderIterator() 
		// TODO Auto-generated method stub
		return null;
	

	@Override
	public Iterator<T> getPreorderIterator() 
		// TODO Auto-generated method stub
		return null;

上述代码相对比较简单，方法注释大部分在接口中已经声明，但是如果仔细去读还是能发现一些问题。

1.通过左右子树来构建一个完整二叉树又两种方法实现，通过构造方法和调用setTree方法，但是二者都调用了私有的方法privateSetTree，再看privateSetTree并没有给出实现。其实原因是这样的，根据不同的情景下可能有多种构建树的方法，这样说比较抽象，下面给出几种privateSetTree的代码以及解释。

private void privateSetTree1(T rootData, BinaryTree<T> leftTree,
			BinaryTree<T> rightTree) 
		root = new BinaryNode<T>(rootData);
		if(leftTree != null && !leftTree.isEmpty())
			root.setLeftChild(leftTree.root);
		
		
		if(rightTree != null && !rightTree.isEmpty())
			root.setRightChild(rightTree.root);

方法非常的简单，在传入参数不为空的情况下new出根节点，并由根节点通过连接左右孩子的方式来完成树的构建。考虑这种情况，我用如下代码完成一个二叉树的构建和中序的输出：

                BinaryTreeInterface<String> eTree = new BinaryTree<String>();
		eTree.setTree("E");
		BinaryTreeInterface<String> fTree = new BinaryTree<String>();
		fTree.setTree("F");
		BinaryTreeInterface<String> gTree = new BinaryTree<String>();
		gTree.setTree("G");
		BinaryTreeInterface<String> hTree = new BinaryTree<String>();
		hTree.setTree("H");
		
		BinaryTreeInterface<String> bTree = new BinaryTree<String>();
		bTree.setTree("B", eTree, fTree);
		
		BinaryTreeInterface<String> cTree = new BinaryTree<String>();
		cTree.setTree("C", gTree, hTree);
		
		BinaryTreeInterface<String> aTree = new BinaryTree<String>();
		aTree.setTree("A", bTree, cTree);
		
		((BinaryTree<String>)aTree).inorderTraverse();

输出的结果如下：

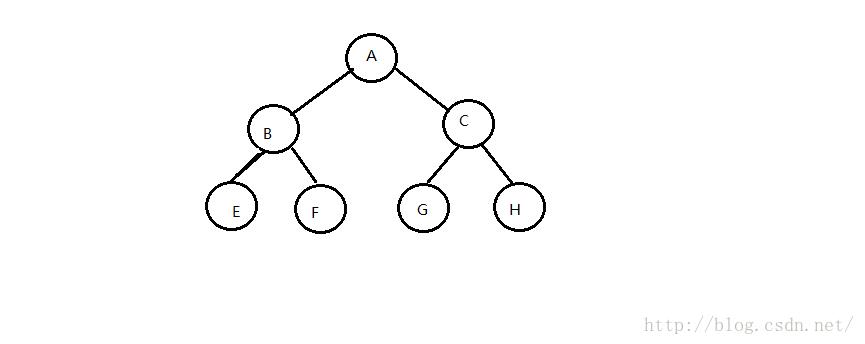
E B F A G C H

中序遍历正确，也验证了我们代码的正确性。但是仔细阅读发现aTree左节点中的root和bTree的root指向了同一地址（因为仅仅传递了指向同一地址的引用），所以如果对bTree的root进行修改的话aTree也会被改变，验证代码：

                BinaryTreeInterface<String> eTree = new BinaryTree<String>();
		eTree.setTree("E");
		BinaryTreeInterface<String> fTree = new BinaryTree<String>();
		fTree.setTree("F");
		BinaryTreeInterface<String> gTree = new BinaryTree<String>();
		gTree.setTree("G");
		BinaryTreeInterface<String> hTree = new BinaryTree<String>();
		hTree.setTree("H");
		
		BinaryTreeInterface<String> bTree = new BinaryTree<String>();
		bTree.setTree("B", eTree, fTree);
		
		BinaryTreeInterface<String> cTree = new BinaryTree<String>();
		cTree.setTree("C", gTree, hTree);
		
		BinaryTreeInterface<String> aTree = new BinaryTree<String>();
		aTree.setTree("A", bTree, cTree);
		
		((BinaryTree<String>)aTree).inorderTraverse();
		System.out.println("-------------------------");
		((BinaryTree<String>) bTree).setRootData("哈哈");
		((BinaryTree<String>)bTree).inorderTraverse();
		System.out.println("-------------------------");
		((BinaryTree<String>)aTree).inorderTraverse();

输出的结果如下：

E B F A G C H
----------------------
E 哈哈 F
----------------------
E 哈哈 F A G C H

可以看出对bTree的修改影响到了aTree。若客户端需要留有之前构造树所用到的子树在今后进行修改重用的话，privateSetTree1方法不可行。

下面给出第二个版本的privateSetTree：

private void privateSetTree2(T rootData, BinaryTree<T> leftTree,
			BinaryTree<T> rightTree) 
		root = new BinaryNode<T>(rootData);
		if(leftTree != null && !leftTree.isEmpty())
			root.setLeftChild(leftTree.root.copy());
		
		
		if(rightTree != null && !rightTree.isEmpty())
			root.setRightChild(rightTree.root.copy());

再次运行之前的测试代码发现一切都正常了，不会因为客户端修改子树而导致构建出来的树发生改变。但是考虑这种方法的效率问题，在大规模构建树时，复制节点的花销会非常巨大。

第三个版本的privateSetTree：

可以把客户端构建树时所用到的子树在构建成功后将其引用置为null，这样就无法操作子树了。

aTree.setTree(a, bTree, cTree);

bTree = null;

cTree = null;

以上代码可以解决可以解决问题，但是会引发新的问题。如果aTree用自己构建自己怎么办？

aTree.setTree(a, aTree, cTree);

aTree = null;

cTree = null;

很显然这样做会破坏新生成的树，不可取！还有一个问题，如果用来构建aTree的两个子树一样怎么办？

aTree.setTree(a, cTree, cTree);

cTree = null;

这样做会使aTree的左右子树指向同一个地址，不可取！

综上，应该按如下的原则来构建树：

左子树的根节点作为新构建树根节点的左孩子连接上，如果右子树与左子树不同，直接作为右孩子连接到根节点，若与左子树相同，则使用副本连接到根节点。若左右子树与新建的树不同，则将左右子树的根节点设置为null。

private void privateSetTree(T rootData, BinaryTree<T> leftTree,
			BinaryTree<T> rightTree) 
		// TODO Auto-generated method stub
		root = new BinaryNode<T>(rootData);
		if(leftTree != null && !leftTree.isEmpty())
			root.setLeftChild(leftTree.root);
		
		
		if(rightTree != null && !rightTree.isEmpty())
			if(rightTree != leftTree)
				root.setRightChild(rightTree.root);
			else
				root.setRightChild(rightTree.root.copy());
			
		
		
		if(leftTree != null && leftTree != this)
			leftTree.clear();
		
		
		if(rightTree != null && rightTree != this)
			rightTree.clear();

对构建树操作的总结：每种方法都有自己的有点与缺点，具体要使用哪种要看在实际工程中的场景，若构建树以后子树没有其他用了，那么直接设为null也就是最好的选择了。若还有其他用途，我们也可以通过复制副本来解决。同样，也可以通过root节点获得某一树的左右子树，如果有兴趣可以自己实现。

上述代码中的setRootData、setRootNode、getRootNode方法之所以没在接口中抽取出来是因为不是所有的实现都会允许客户端做这种修改。

以上对树的各种顺序遍历只采用了最基本的输出，同时也使以递归的形式进行调用，在下一篇文章中将会使用非递归方式对树进行顺序遍历，以及对遍历情况做分析~

以上是关于java二叉树的实现的主要内容，如果未能解决你的问题，请参考以下文章

用java实现二叉树的遍历算法

基于Java的二叉树的三种遍历方式的递归与非递归实现

Java 剑指offer(55-2) 平衡二叉树

二叉树相关知识总结

二叉树的镜像(反转二叉树)

Java实现二叉树地遍历求深度和叶子结点的个数