决策树——ID3算法

Posted 2022-12-10 joker-yan

前言

我们在使用数据挖掘的时候，完成数据的“清洗”等一系列繁琐的步骤，就可以对数据进一步地进行“挖掘”——对数据进行分类的建立、预测、聚类分析等等的操作。在分类和预测的过程中，有一系列的算法得以脱颖而出——“回归分析”、“决策树”、“人工神经网络”等等

---

那么今天我就来介绍一下”决策树“——ID3算法

一、ID3算法

ID3作为一种经典的决策树算法，是基于信息熵来选择最佳的测试属性，其选择了当前样本集中具有最大信息增益值的属性作为测试属性。
样本集的划分则依据了测试属性的取值进行，测试属性有多少种取值就能划分出多少的子样本集；同时决策树上与该样本集相应的节点长出新的叶子节点。
ID3算法根据信息论理论，采用划分后样本集的不确定性作为衡量划分样本子集的好坏程度，用“信息增益值”度量不确定性——信息增益值越大，不确定性就更小，这就促使我们找到一个好的非叶子节点来进行划分。

二、ID3算法的基本原理以及实例分析

1.我们假设一个这样的数据样本集S，其中数据样本集S包含了s个数据样本，假设类别属性具有m个不同的值（判断指标）：C_i(i=1,2,3,…,m)

S_i是C_i中的样本数，对于一个样本集
总的信息熵为：

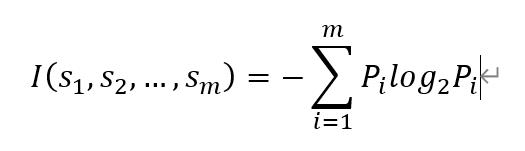
其中，P_i表示任意样本属于C_i的概率，也可以用s_i/s 进行估计。
我们假设一个属性A具有k个不同的值 a₁,a₂,…,a_k, 利用属性A将数据样本S划分为k个子集S₁，S₂，…， S_k，其中S_j包含了集合S中属性A取a_j值的样本。若是选择了属性A为测试属性，则这些子集就是从集合S的节点生长出来的新的叶子节点。
设S_ij是子集S_j中类别为C_i的样本数，则根据属性A划分样本的信息熵值为：

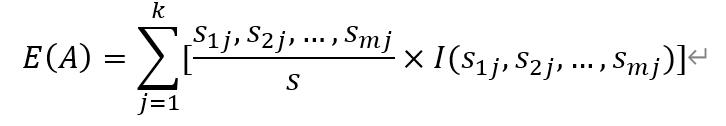
最后，我们利用属性A划分样本集S后得到的信息熵增益为：

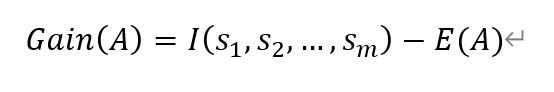
2.实例分析

我们假设有这么一个案例，小学校门口总是会出现一些零食小贩，判断某一天这些零食小贩的收入是否良好可以依据很多因素，如：天气、学生是否放假、保安是否打压、是否进行活动促销等等多个属性来衡量。
对于天气属性，我们将是否下雨作为一个天气好坏的叛别，则天气具有“好”与“不好”两种属性值；
学生是否放假也有两种属性值“是”与“否”；
保安是否打压也分为“好”与“不好”；
活动促销的两种属性值为“是”与“否”
而对于小贩的收入，我们假设取全年的平均收入为平均值，高于平均值为“高”，否则为“低”。
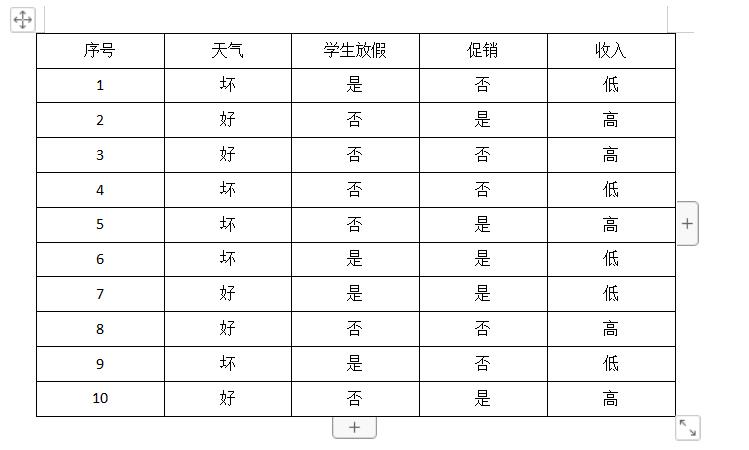
由此，我们得到了这样的一个表格：

计算过程：
首先，我们先计算总的信息熵，其中共有10条记录，收入为“高”有5条，收入为“低”也有5条
步骤1 总信息熵:

下面计算各个属性的信息熵:
步骤2 天气属性：
天气好的情况下，收入为“高”的记录为4条，收入为“低”的记录为1条，可以表示为(4,1)；天气不好的情况下，收入为“高”的记录为1条，收入为“低”的记录为4条,可以表示为(1,4).
则天气属性的信息熵的计算过程如下：



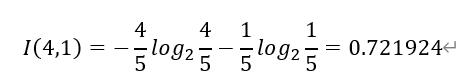
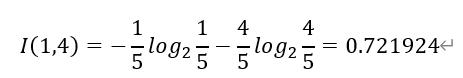
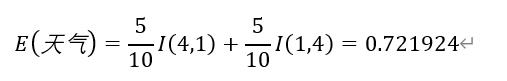
步骤3 学生放假属性：
学生放假时，收入为“高”有0条，收入为“低”有4条。记为（0,4）；
学生不放假时，收入为“高”有5条，收入为“低”有1条。记为（5,1）；

学生放假属性的计算过程为：

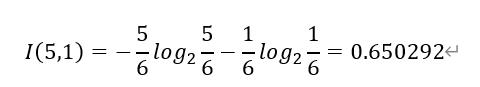
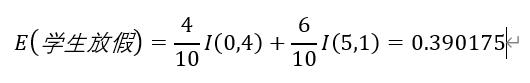
步骤4 促销属性：
当小贩进行促销时，收入为“高”有3条，收入为“低”有2条。记为（3,2）；
当小贩不进行促销时，收入为“高”有2条，收入为“低”有3条。记为（2,3）；
促销属性的计算过程为：

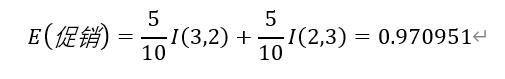
步骤5 计算信息增益值



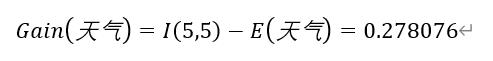
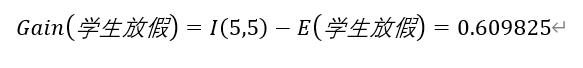
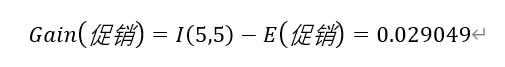
由步骤4可以知道“学生放假”的信息增益值最大，所以以“学生放假“为节点进行划分，划分为两个分支分别为“是”、“否”（指学生是否放假），然后再循环进行步骤1 ~步骤5的过程（排除已经进行划分的节点步骤），对剩下的2个节点分支进行划分，再进行信息增益的计算。

直至无法形成新的节点，从而生成一棵“决策树”。

ID3算法参考了《python数据分析与挖掘实战》中关于ID3算法的解释，感兴趣的可以前往观看。

总结

ID3算法是经典的决策树算法，但是随着时间的发展，出现的C4.5算法弥补了许多ID3算法在使用信息增益率来选择节点属性的不足之处。
感谢各位的观看，望斧正。