数据结构与算法:树赫夫曼树

Posted 2022-12-10 史大拿

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构与算法:树赫夫曼树相关的知识，希望对你有一定的参考价值。

Tips: 采用java语言,关注博主,底部附有完整代码

工具:IDEA

本系列介绍的是数据结构: 树

这是第5篇目前计划一共有11篇:

敬请期待吧~~

高光时刻

基本了解

构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树/赫夫曼树 (Huffman Tree)。赫夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

赫夫曼树

权

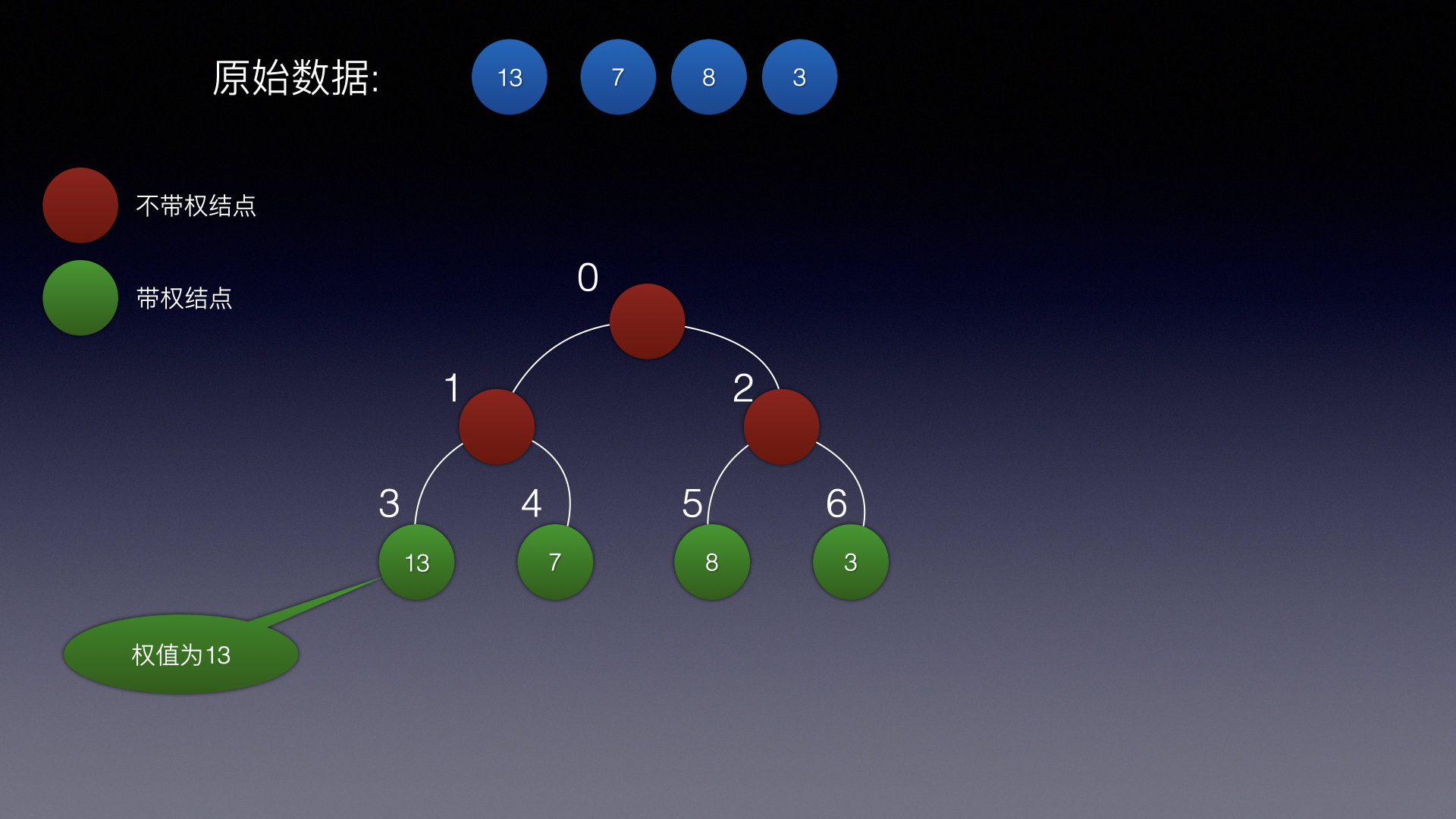
**权 **就是通过一个特殊的变量来标识,如果这个变量存在,那么就是带权结点,反之是不带权结点

图中绿色的就都是带权结点,红色则是不带权结点

路径

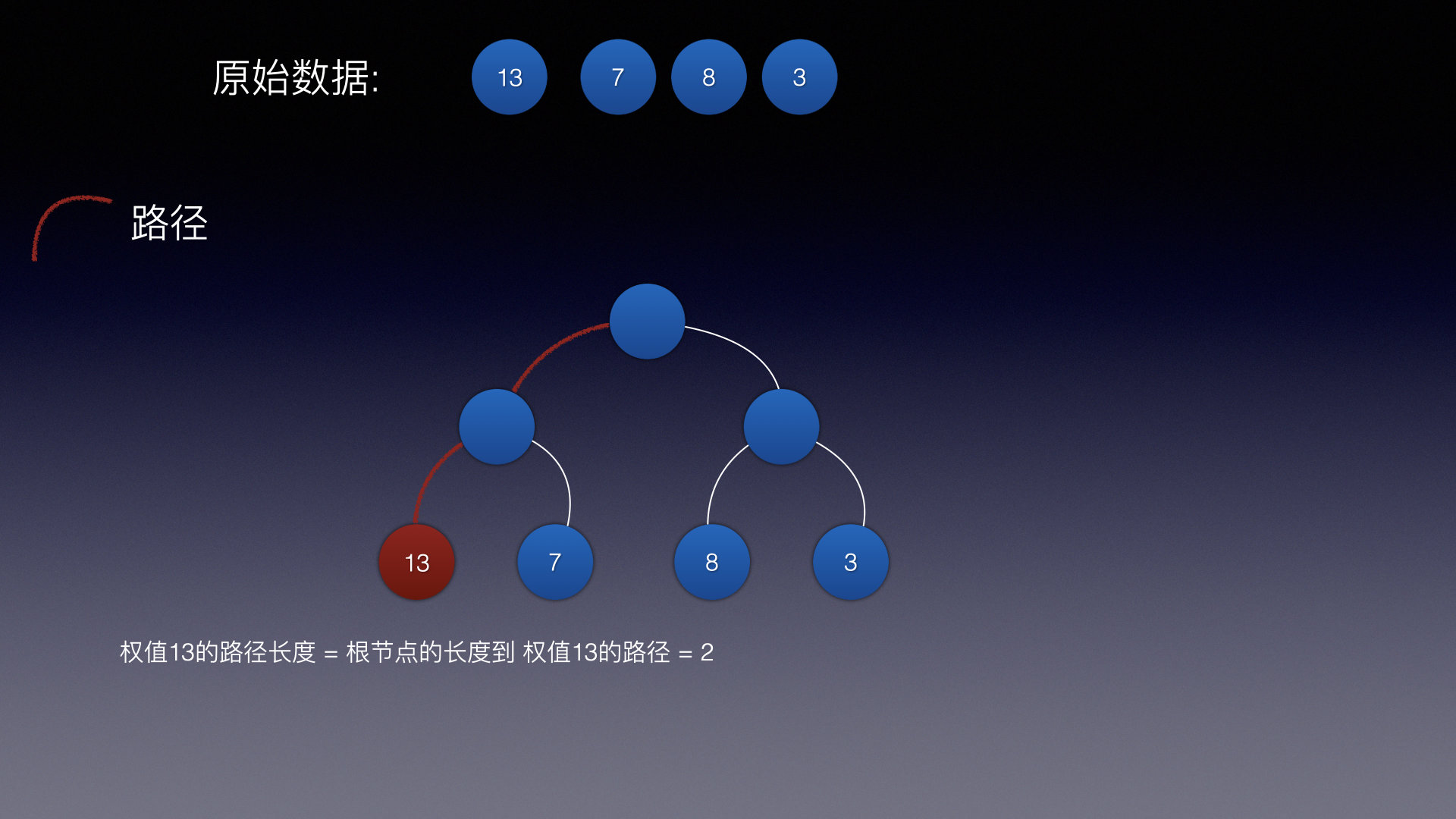
路径就是根节点到权的距离

例如13的路径长度就是2

WPL(weighted path length):

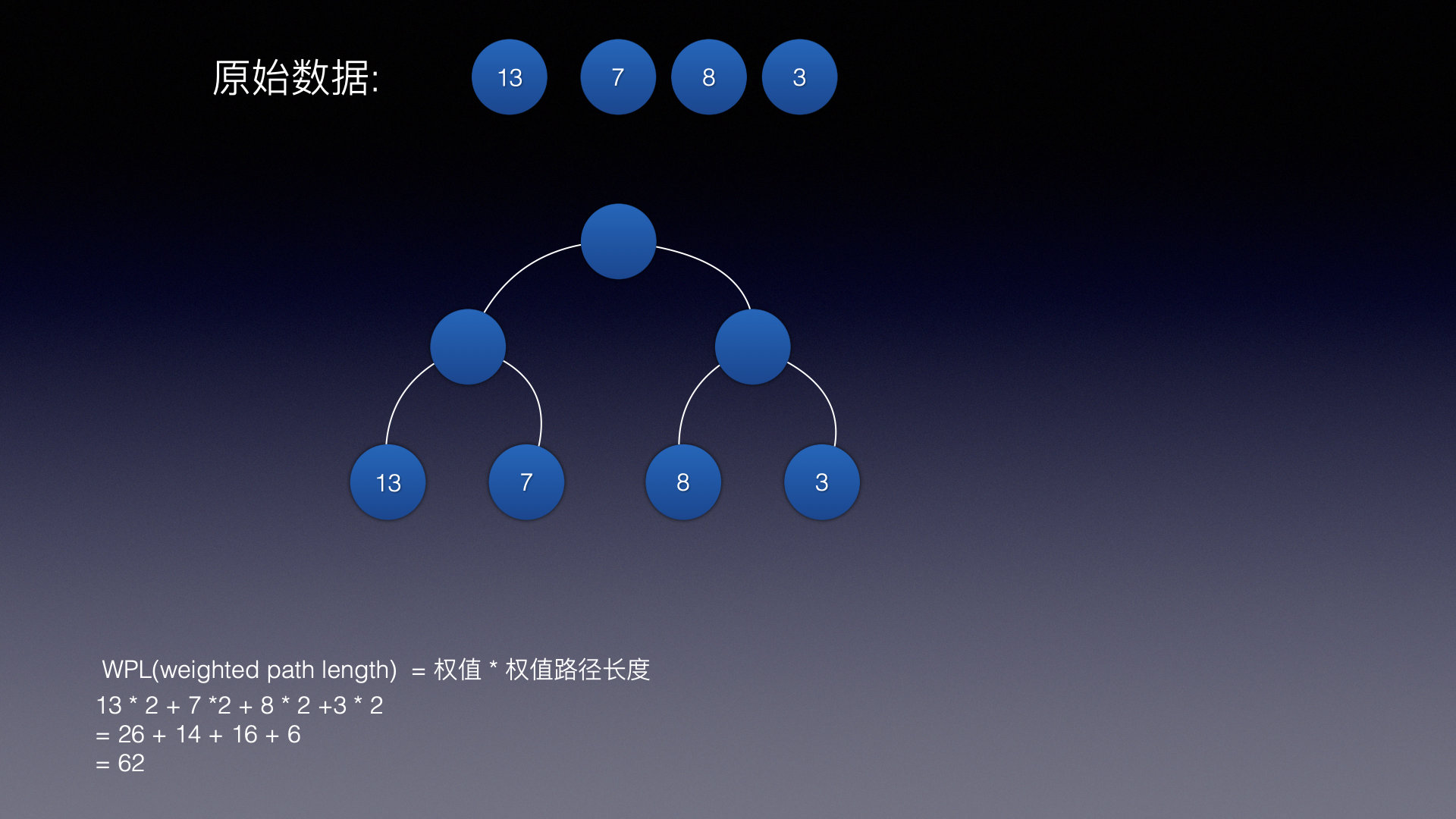
WPL 是所有权 * 所有路径长度相加之和

例如这张图中WPL 就是62

赫夫曼树是WPL最小的树

普通的赫夫曼树

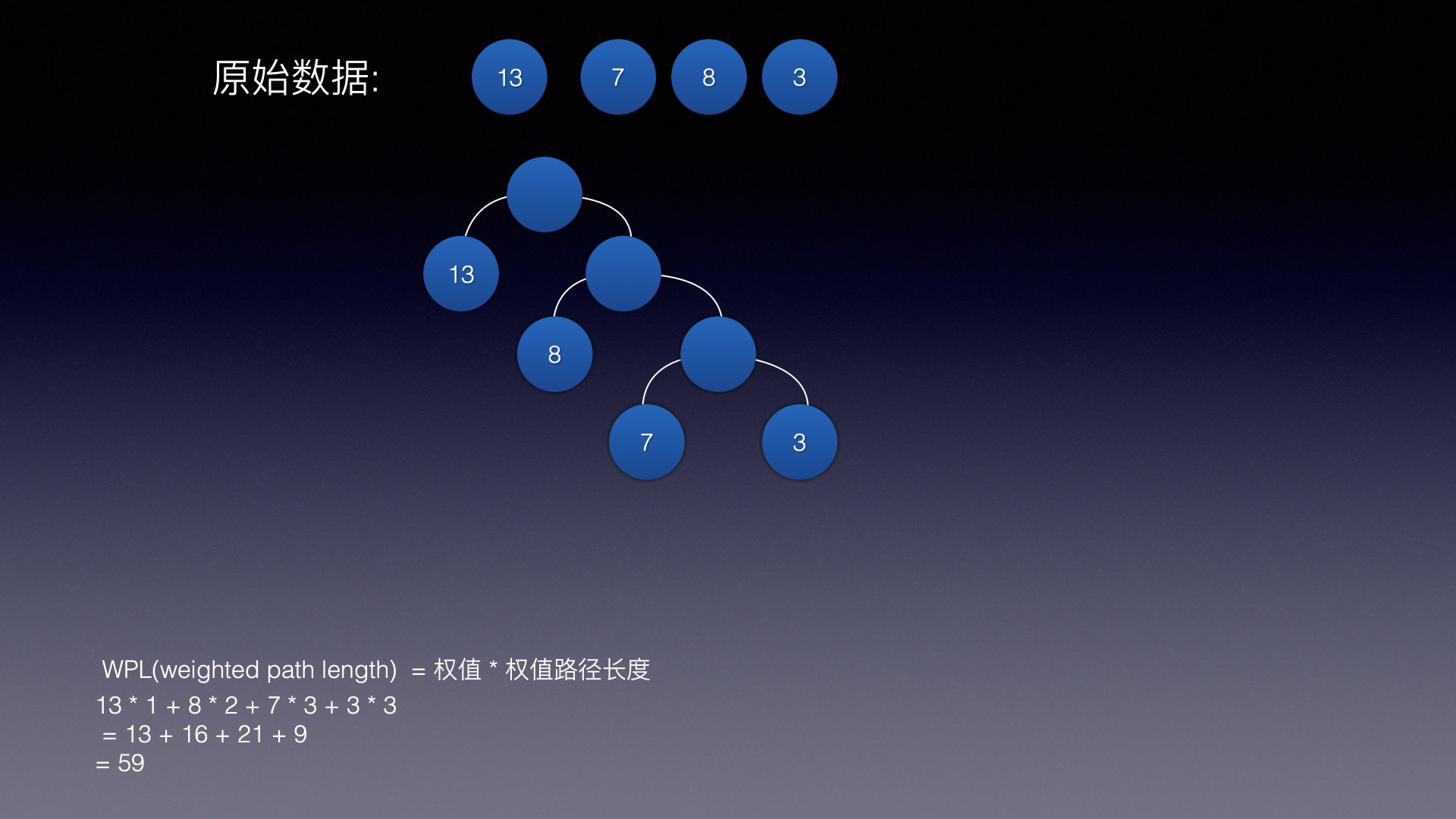
这就是一颗很常见的赫夫曼树,可以看出,权值越大的结点,离根节点越近

构建赫夫曼结点

创建赫夫曼结点:

class HuffmanNode implements Comparable<HuffmanNode> 
    // 权值
    public int value;
    // 左子结点
    public HuffmanNode leftNode;
    // 右子结点
    public HuffmanNode rightNode;

    public HuffmanNode(int value) 
        this.value = value;
    

	  // 前序遍历
    public void show() 
        System.out.println(this);
        if (leftNode != null) 
            leftNode.show();
        
        if (rightNode != null) 
            rightNode.show();
        
    

    @Override
    public String toString() 
        return String.valueOf(value);
    

    @Override
    public int compareTo(HuffmanNode o) 
        // 正序
        return value - o.value;

这里用到了Comparable,用来排序,这是java基础,很久不用记忆模糊的同学可以自行百度一下~

假设当前需要将 13, 7, 8, 3, 29, 6, 1 转变成赫夫曼树

先来看看完整流程:

可以看出,如果是纯数组的话,一定都是带权结点

分析

根据上面的流程图可以看出

如果想要吧数组转变成赫夫曼树,

那么需要将数组排序

依次取出前两个生成一个新的结点,

然后再排序,在生成新的结点

最终留下一个结点,就是根节点

思路很简单,来看一眼完整代码

完整代码

public class Client 
    public static void main(String[] args) 
        int[] ints = 13, 7, 8, 3, 29, 6, 1;

        HuffmanNode root = createHuffmanTree(ints);
        System.out.println("获取到的跟节点为:" + root);
        root.show();
    

    /*
     * @author: android 超级兵
     * @create: 2022/6/10 20:01
     * TODO 创建huffman树
     */
    public static HuffmanNode createHuffmanTree(int[] ints) 
        // 将数组转变成Huffman结点
        ArrayList<HuffmanNode> huffmanNodes = toOrderlyList(ints);

        System.out.println("赫夫曼树结点为:" + huffmanNodes);

        while (huffmanNodes.size() > 1) 
            // 排序
            Collections.sort(huffmanNodes);

          	// 取出2个即结点
            HuffmanNode leftNode = huffmanNodes.get(0);
            HuffmanNode rightNode = huffmanNodes.get(1);

            // 生成跟节点
            HuffmanNode parentNode = new HuffmanNode(leftNode.value + rightNode.value);
          
            // 设置结点
            parentNode.leftNode = leftNode;
            parentNode.rightNode = rightNode;

            // 删除已经使用的结点 为了获取最终的root结点
//            huffmanNodes.remove(leftNode);
//            huffmanNodes.remove(rightNode);

            // 删除已经使用的结点
            huffmanNodes.remove(0);
            huffmanNodes.remove(0);

            // 添加结点到集合中
            huffmanNodes.add(parentNode);

            System.out.println("当前结点为:" + huffmanNodes);
        

        return huffmanNodes.get(0);
    

    /*
     * @author: android 超级兵
     * @create: 2022/6/10 19:56
     * TODO int[] 转 List<HuffmanNode>
     */
    public static ArrayList<HuffmanNode> toOrderlyList(int[] ints) 
        ArrayList<HuffmanNode> list = new ArrayList<>();

        for (int element : ints) 
            list.add(new HuffmanNode(element));
        

        return list;