Shader笔记——3D数学基础

Posted 2023-04-17

参考技术A

在3D世界中，为了确定不同顶点所在的位置，需要使用坐标表示，二坐标的数值是基于一个固定的参照点进行定位的，这个点就是坐标原点。

通常情况下，原点的坐标一般都是（0，0）。

如果把所有的坐标汇集在一起管理，那就构成了一个坐标系。一个完整的坐标系会包含原点，方向和坐标。

3D中涉及各种坐标系，从维度进行区分，所有坐标系可以分为平面直角坐标系和空间直角坐标系。

在空间坐标系中，根据坐标方向的不同又可以分为左手坐标系和右手坐标系。

若将大拇指设定为x轴，食指设定为y轴，中指设定为z轴，左右手坐标系如图：

在数学中，坐标属于标量，只表示大小，不表示方向。
而同时表示长度和方向信息的，称之为向量（Vector），或者叫“矢量”。顶点的法线向量，切线向量等都是向量。

假设二维向量 a 的起点A，终点为B，使用B的坐标减去A的坐标，即可计算出个向量 a 。
二维向量 a 的计算公式如下：

若将公式推广到三维空间，假设三维向量 a 的起点A，终点B，则三维向量 a 的计算公式如下：

如果俩个向量的长度相等但方向相反，则这俩个向量互为相反向量。

零向量的相反向量是它本身。

从几何的角度来讲，将一个向量的起点作为终点，而原本的终点作为起点，最终得到的向量就是原向量的相反向量。

假设向量 a 的起点A，终点B， a 的相反向量 b ，表示如下：

向量包含长度和方向，向量的长度被称为向量的模。如向量 a 的模表示为| a |。

如图通过勾股定理，求得

二维向量 a 的模长计算公式为：

如图通过俩次勾股定理，求得

“单位向量”是指模长为1的向量。
在很多情况下向量的方向比向量的长度更值得关注，如灯光的照射方向，摄像机的查看方向等。为了计算方便，可将这种向量转变为单位向量，这个转变的过程称为向量的标准化（Normalize）。

从代数的角度来讲，一个非零向量除以自身的长度，既可以将自身长度缩放为1。零向量的长度为0，在数学中0作为被除数没有意义。
因此非零向量 a 的标准化向量为：

单位向量与原向量相比，只是长度发生了改变，方向保持不变。

从几何的角度来讲，向量的加法运算满足三角形法则。

向量的加法运算可以推广到多个数量相加，最终结果是从第一个向量的起点指向最后一个向量的终点，长度为起点与终点之间的距离。

从代数的角度来讲，向量的加法就是将相同的分量进行相加。

向量的减法运算可以理解为一向量与另一向量的相反向量做加法运算，同样满足三角形法则。
向量 a 和 b 的减法运算转变为与相反向量的加法运算：

相同起点的俩个向量相减，得到的向量为第二个向量的终点指向第一个向量的终点，长度为俩终点之间的距离。

从代数的角度来讲，向量的减法运算就是将相同的分量相减。计算公式如下：

将向量乘以一个标量，可产生向量缩放的效果。如图：

假设向量 a =(x,y,z),向量缩放k倍公式为：

向量 a 和 b 的点积写作 a . b 。
在代数中，点积又叫做内积，俩个向量点积的结果就是对应所有分量相乘之后的和。点积的结果是数值。
点积计算公式为：

在几何中，俩个向量点积的结果就是一个向量在另外一个向量上的投影长度与这个向量长度的积。
点积的计算公式为：

向量的叉积又称为外积，叉积的结果是向量。向量 a 和 b 的叉积写作 a × b 。
叉积的计算公式为：

在几何中，叉积得到的向量与 a 和 b 所在平面垂直，长度等于向量 a 和 b 组成的平行四边形的面积，该向量被称为法向量。如图：

假设将叉乘的俩个向量颠倒顺序， b 与 a 叉乘所得向量的方向将会朝下。

常用的向量运算法则如下所示：

向量可以使用横向排列的数组表示，假设纵向上继续排列相同维度的数组，最后组成的数组就是——矩阵(Matrix)。

向量的维度表示表示该向量所包含数的个数，同样的，矩阵的维度表示了该矩阵所包含的行和列的数量。通常使用r(raw的首字母缩写)表示行数，使用c(column的首字母缩写)表示列数，而矩阵本身则使用黑斜体大写字母表示，如 M 。
一个3×3的矩阵 M 以及所对应的所有分量可以如下表示：

行数和列数相等的矩阵称为方阵。
方阵中行号和列号相等的分量称为对角元素，其他分量称为非对角元素。非对角元素全为0的矩阵称为对角矩阵。

在对角矩阵中，对角元素全为1的矩阵叫作单位矩阵。

任何矩阵乘以单位矩阵，最终得到的结果与原矩阵相同。单位矩阵对于矩阵的作用就像1对于标量的作用一样。

假设将一个r×c的矩阵 M 沿着对角线翻转，得到的新矩阵称为矩阵 M 的转置矩阵（Transpose Matrix）。

转置矩阵的重要法则：将一个矩阵转置之后再进行转置，得到的矩阵与原矩阵相同，公式如下：

跟向量类似，矩阵也可以与标量相乘，中间不需要写运算符号，相乘之后的结果与原矩阵维数相同，然后将每个分量乘上这个标量。公式如下：

当第一个矩阵的列数等于第二个矩阵的行数，这俩个矩阵才可以相乘，得到矩阵的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。

在Shader中，向量也可以与矩阵相乘，相乘的时候可以把向量看作行数为1或列数为1的矩阵。

向量(x,y,z)可以横向写成1×3的矩阵，被称为行向量：

也可以写成3×1的矩阵，被称为列向量：

向量与矩阵相乘的几何意义是实现向量的空间变换。

在3D中，所有的变换都是通过矩阵完成的，包括常用的平移，旋转，缩放，除此之外，还有坐标空间之间的变换也是通过矩阵完成的。

假设向量 v = (x,y,z)，可以表示为

假设平面坐标系的俩个坐标向量分别为 p = (1,0), q =(0,1),绕原点逆时针旋转角度之后如图：

左右手坐标系中的旋转方向完全不同，俩种坐标系中的旋转方向的判断方法：先伸出与坐标系对应的那只手，握住旋转轴并且保持大拇指的朝向与旋转轴的正方向一致，其余四指的朝向即为旋转的正方向。如图，弧线箭头所示的方向即为右手坐标系的旋转正方向。

左右俩种坐标系对应的旋转方向归纳如下：

这里只讲解绕坐标轴旋转的情况。
将空间坐标系绕x轴旋转，空间坐标系中的旋转方向如图：

x轴上的所有坐标都不会发生改变，从x轴正方向朝负方向观察坐标系，y轴和z轴的旋转情况完全跟平面坐标系的旋转情况一样，如图：

最终绕x轴旋转角度的变换矩阵为：

空间坐标系绕y轴的旋转方向如图：

从y轴正方向朝负方向观察坐标系，x轴和z轴的旋转情况如图：

空间坐标系绕z轴的旋转方向如图：

从z轴正方向朝负方向观察坐标系，x轴和y轴的旋转情况如图：

UE5 Shader基础学习笔记——01-12 图形管线/创建shader/数学节点/贴图压缩/LerpDotUV/常用向量/坐标空间/MinMaxClampSaturate/法线贴图混合

UE5 Shader基础学习笔记——01-12 图形管线/创建shader/数学节点/贴图压缩/LerpDotUV/常用向量/坐标空间/MinMaxClampSaturate/法线贴图混合

• Lec01-02 The Graphics Pipeline 图形管线
• Lec03 First Shader 第一个shader
• Lec04 Basic Shader Math 基础数学节点
• Lec05 Understanding Texture Maps 贴图压缩设置
• Lec06 Lerp 线性插值
• Lec07 Dot 点乘 (etc.菲涅尔/灰度)
• Lec08 UV 纹理坐标
• Lec09 Input Vector 视线法线光线 (etc.远近mask)
• Lec10 View, World, Object, & Tangent Space 坐标空间 (etc.matcap,法线混合)
• Lec11 Min Max Clamp Saturate 最大最小钳制饱和
• Lec12 Blending Normal Maps 法线贴图混合方法

本系列学习资料来源，Ben Cloward的油管空间，本笔记主要对其中UE的部分进行记录

Lec01-02 The Graphics Pipeline 图形管线

Lec01 主要介绍一下这个系列的内容，该系列会从基础的单个节点的功能，到组合使用，由浅入深讲解Shader的技巧，同时对UE5和Unity一起讲解

Lec02 简要介绍了下渲染管线

• 我们在使用UE Unity maya等3D软件时，在CPU中产生3D数据， 通过Directx/Opengl 传递vertex data到图形驱动程序，驱动接着传递数据到GPU前端。
• 接着数据会传递到可编程的顶点处理器，也就是vertex shader起作用的地方，在这个地方会处理顶点数据。
  一个Vertex包括很多信息的组合（顶点位置，UV坐标，顶点色，法线等）。
  该部分顶点处理的功能，主要实现坐标系统变换，将信息从Object Space变换到Screen Projection Space，这样Vertex信息可以绘制到屏幕上。
  除了坐标变换的基本功能，在这一部分还可以做一些其他功能，比如顶点动画，UV动画，法线调整，计算一些信息存在顶点色中。
  当顶点处理器刚诞生时，GPU的大部分工作都会在里面实现，但到了现在，顶点处理阶段通常只会处理顶点变换，大部分魔法效果会在像素处理阶段的pixel shader实现，不过如果有些效果可以在顶点处理阶段实现则会节省性能
• 接着实现的是图元装配，把所有顶点装配成形状，接着光栅化和插值单元，转换成屏幕上的像素。
• 接着进入可编程的像素处理器，也就是pixel shader起作用的地方，使用来自CPU的信息和vertex shader操作后的信息一起输出效果，最后再经历一些最终的光栅操作。
• 以上是前向管线的做法，现代大部分使用延迟管线，也就是pixel shader输出颜色，法线，金属遮罩，粗糙度，写进g buffer，再进行最后的光照计算

进入引擎中，下面是直接采样和进行了UV动画的指令数差距，可以看到差了四个指令


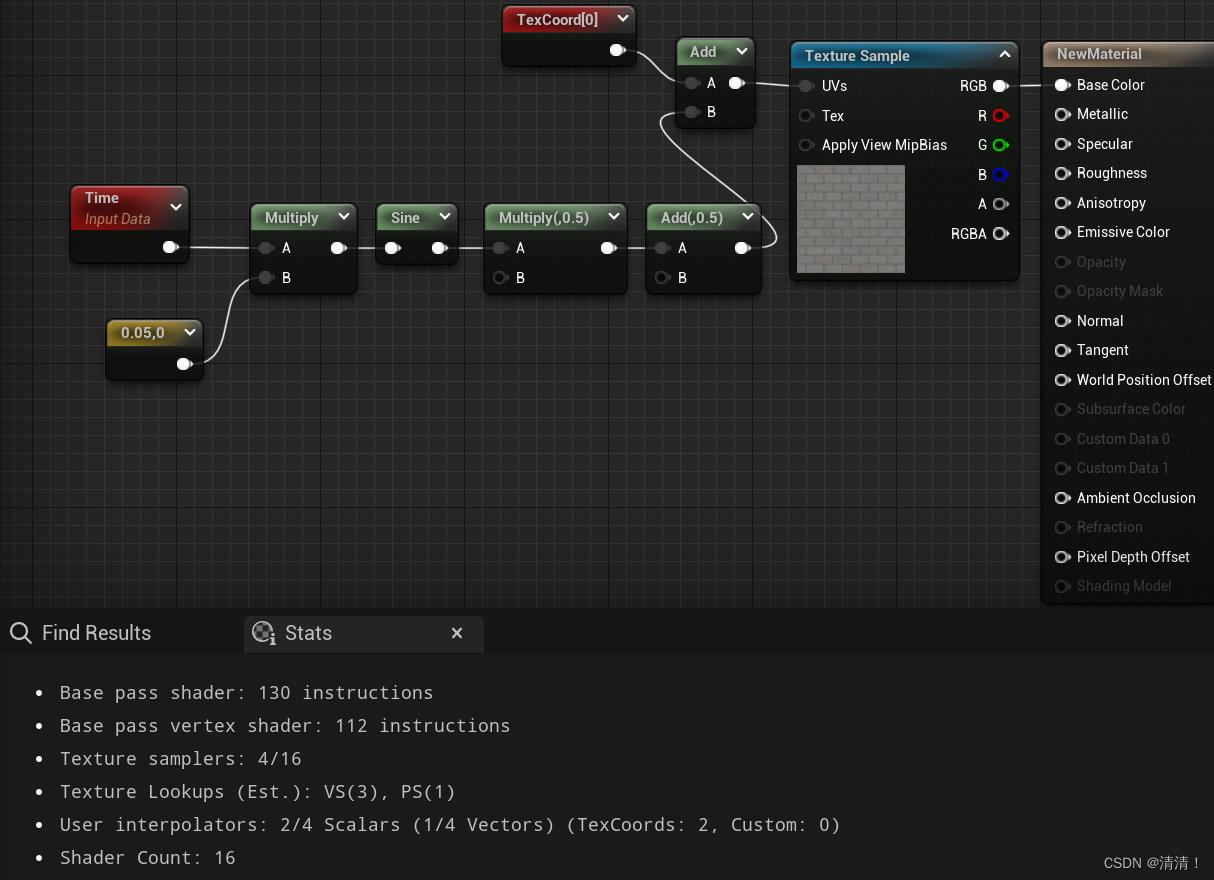
有一种可以节省性能的方法是可以将计算动画的步骤挪到vertex shader中，可以使用vertex interpolator进行顶点插值，可以看到vertex shader的步骤多了四条，另外world position offset也是在vertex shader中实现的

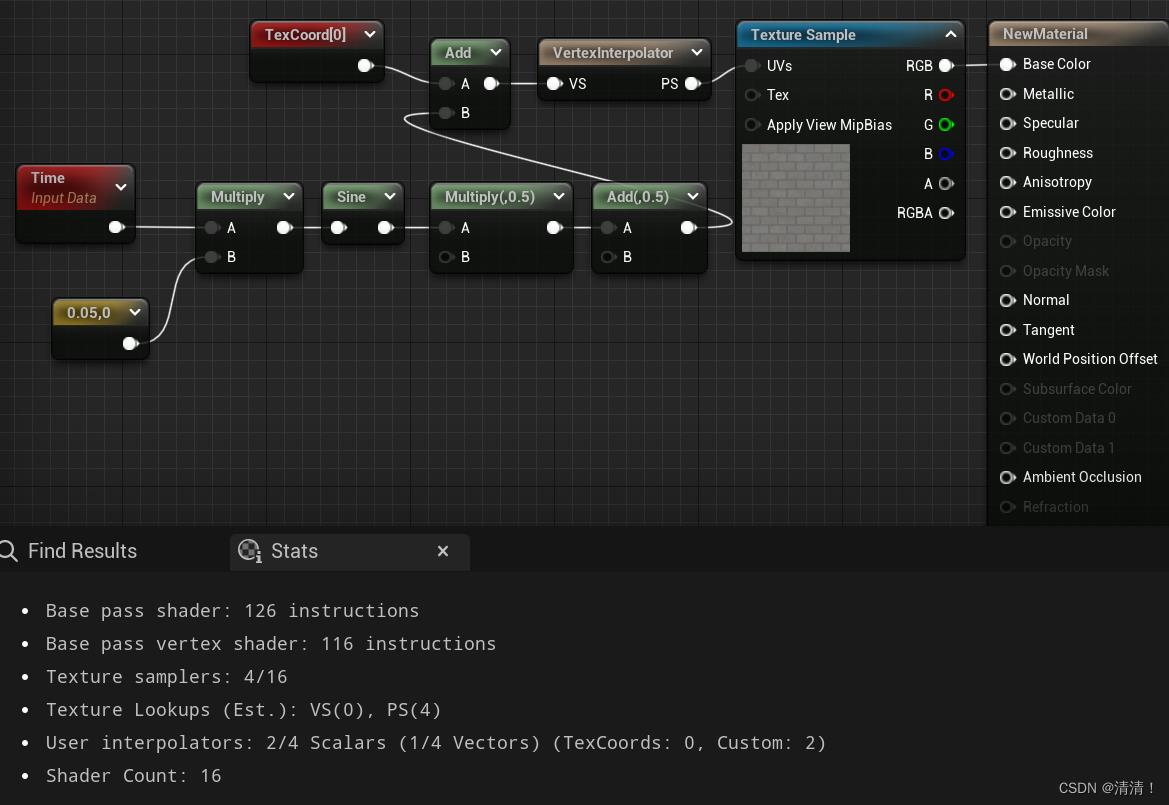
Lec03 First Shader 第一个shader

主要讲了怎么创建项目，以及界面UI相关
在UE中可以使用Tool→Debug→WidgetReflector调整界面文字大小

Lec04 Basic Shader Math 基础数学节点

可以复习以前的PBR和数据类型相关内容
UE4 Material 101学习笔记——01-07 介绍/PBR基础/UV扭曲/数据类型/翻页动画/材质混合/性能优化

介绍了UV，time，add，subtract，multiply，divide，one minus

Lec05 Understanding Texture Maps 贴图压缩设置

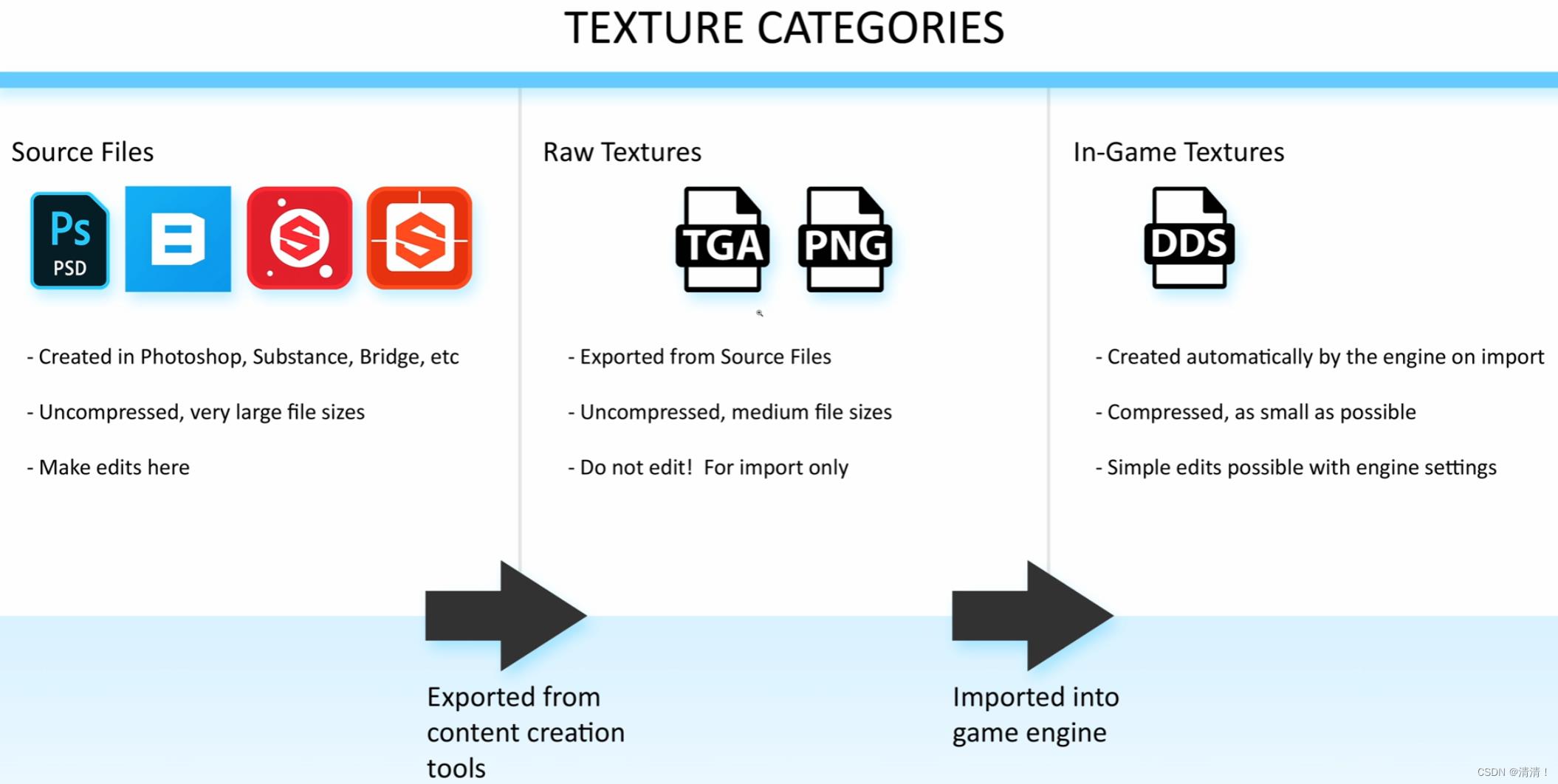
• 对于贴图，设计师在外部软件设计编辑，处理的是未经压缩的文件
• 创建完成后贴图被转换为不再被编辑的中间格式（tga，png等）
• 导入游戏引擎时，引擎自动生成压缩后的图像格式，这些是会真正被加载到内存中的

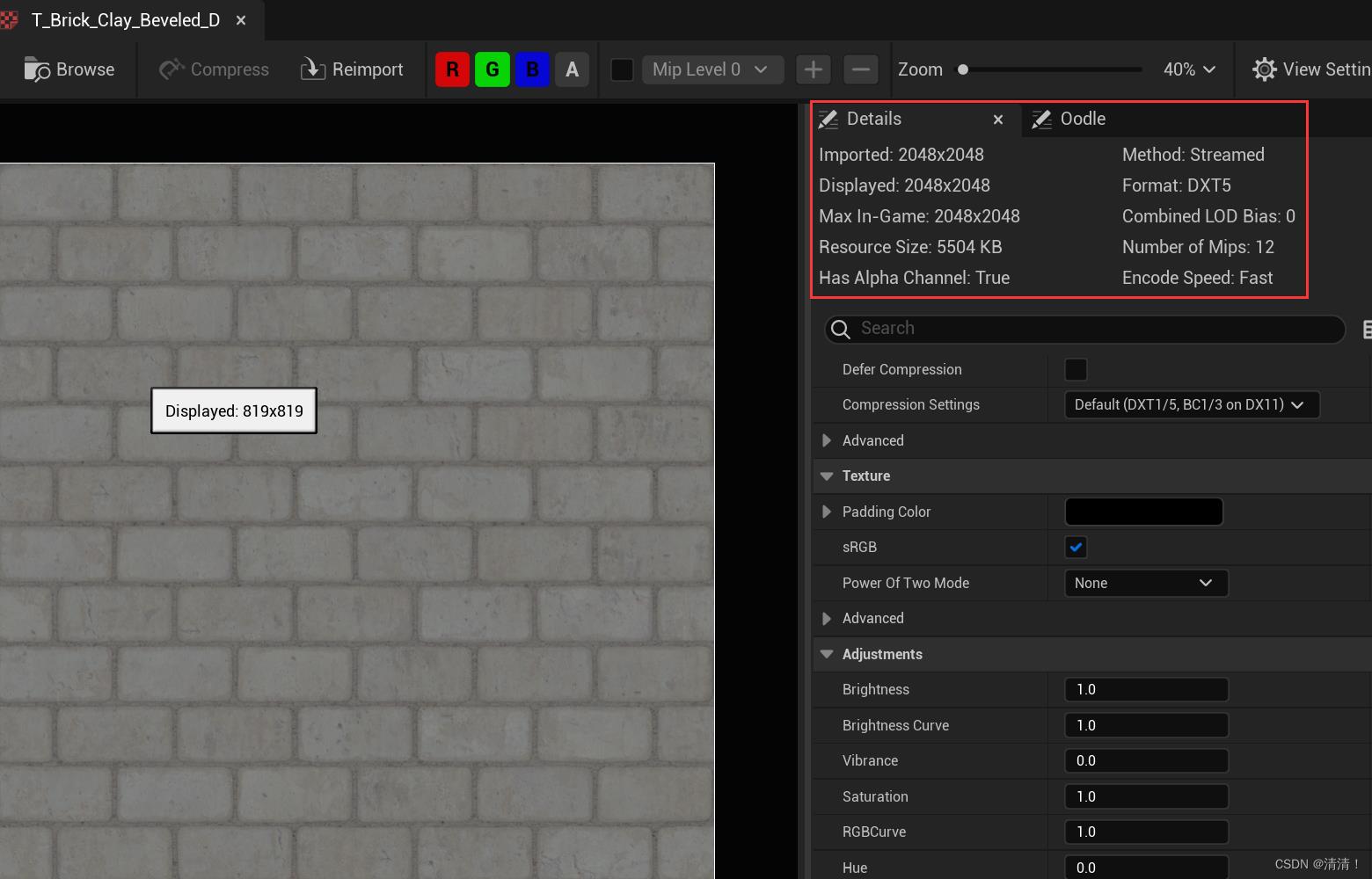
贴图压缩大致参考（单位KB），左三种是压缩的，右三种是不压缩的
DXT1支持三通道压缩，DXT5支持四通道压缩，BC7支持三或者四通道

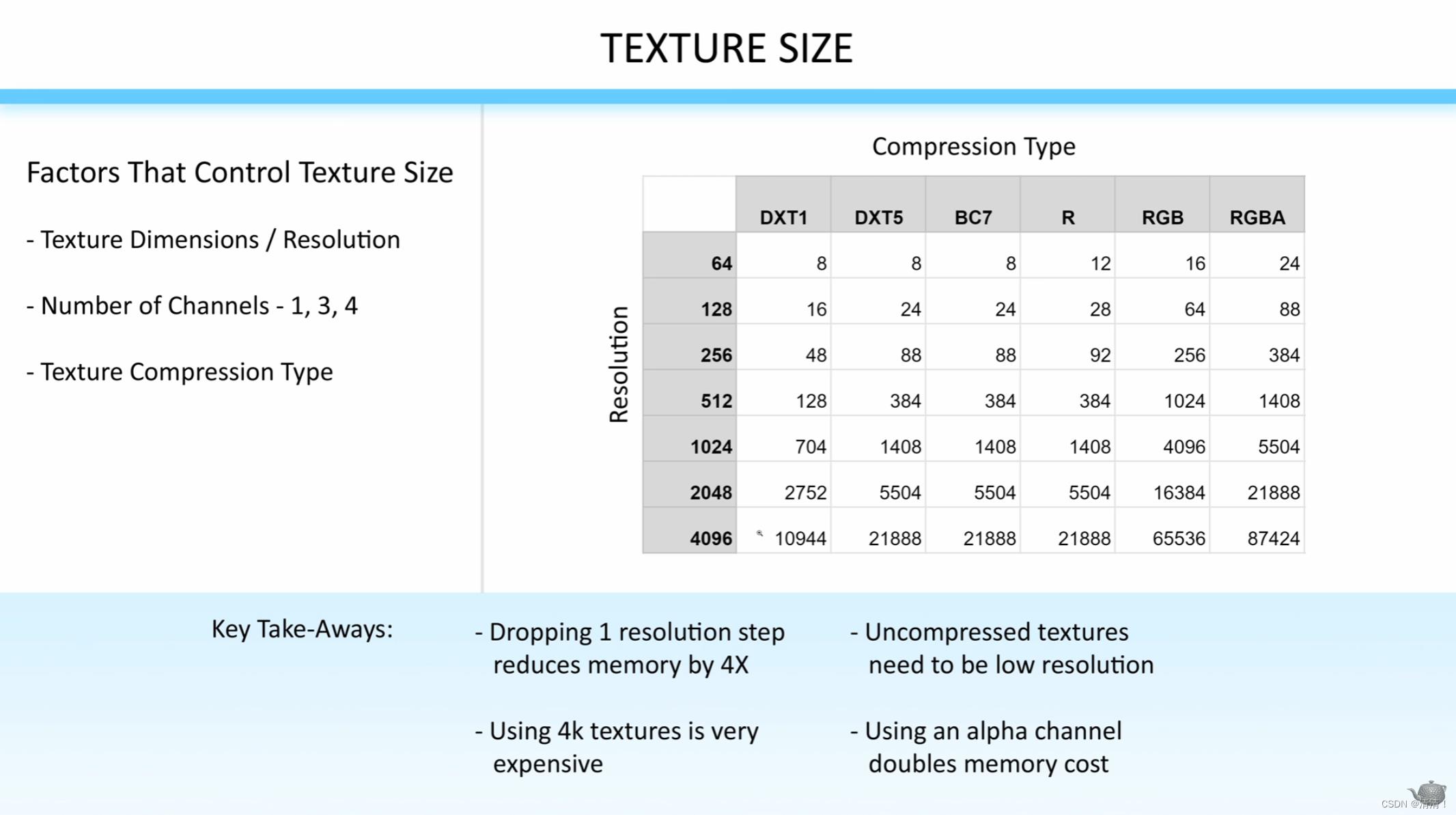
• 图中一级分辨率内存约差4倍 / 未压缩的贴图如果要使用，需要降低分辨率 / 4k纹理消耗很大 / 在压缩纹理中，使用A通道会使内存翻倍
• 在引擎中，可以调整贴图分辨率
  
  也可以选择是否使用A通道，可以看到不用A通道压缩少了一半
  
  如果不想压缩，可以在CompressionSettings选择UserInterface2D，可以看到Format变成B8G8R8A8，内存大小显著上升
  
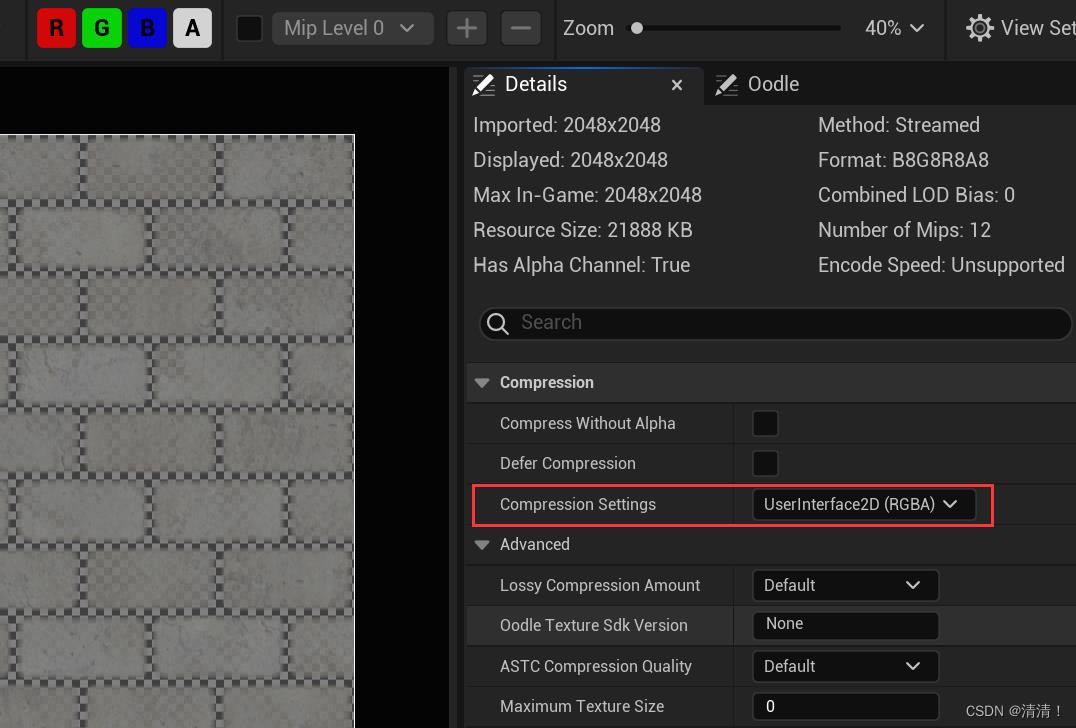
  单通道可以选择Grayscale压缩去掉sRGB，对于彩色图案需要在Texture栏下勾上sRGB，法线则选择Normalmap

纹理在导入时也会生成Mipmaps，引擎会根据需要自动生成选择什么层级的Mipmap

Lec06 Lerp 线性插值

Lerp节点

$Lerp(y_1,y_2,weight)=(1-weight)\ast y_1+weight\ast y_2$

Lec07 Dot 点乘 (etc.菲涅尔/灰度)

Dot点乘
GAMES101课程学习笔记—Lec 02：Linear Algebra 线性代数回顾
一些点乘的例子，N dot V

灰度算法

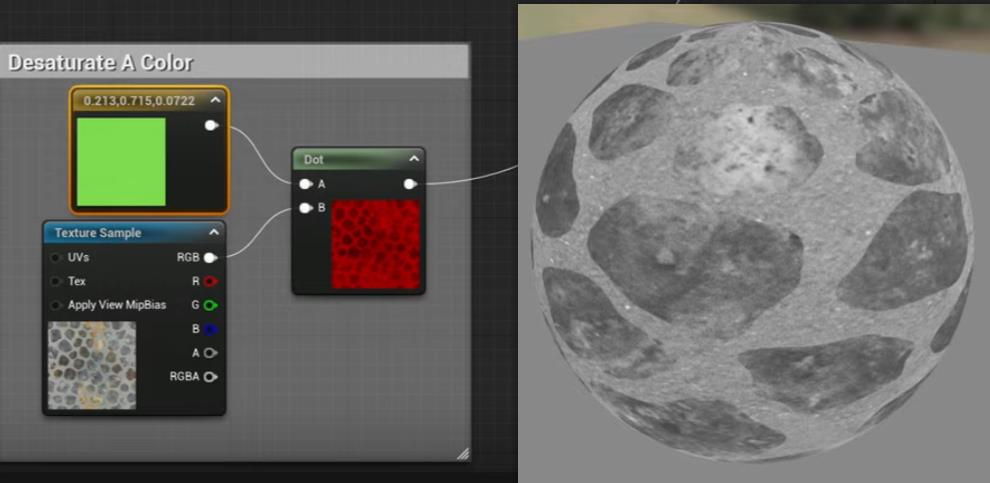
充当mask

Lec08 UV 纹理坐标

解释啥是UV
GAMES101课程学习笔记—Lec 07~09：Shading 定义、着色模型、着色频率、图形渲染管线、纹理


UV坐标可以加减进行移动，乘除进行缩放

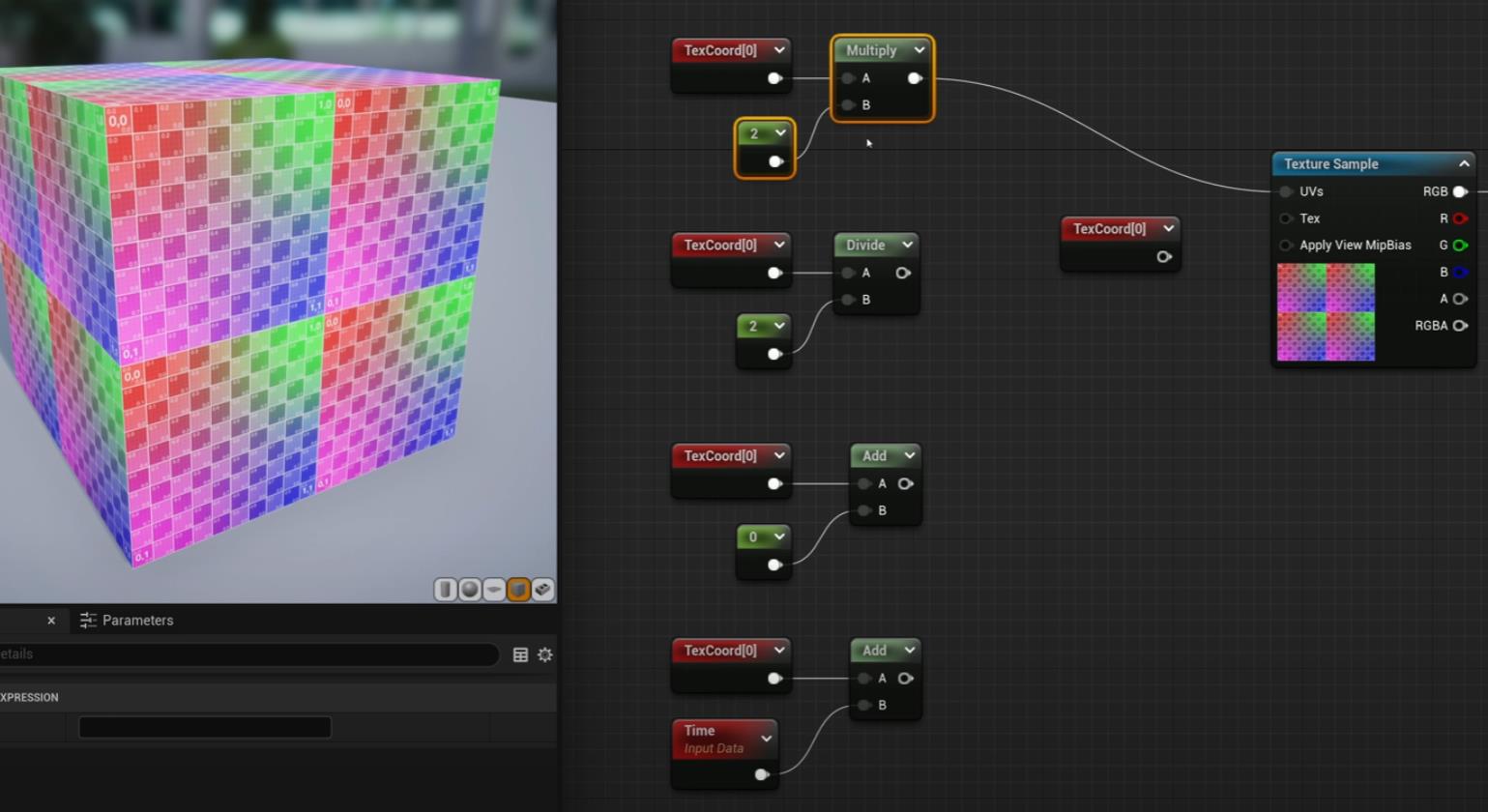
Lec09 Input Vector 视线法线光线 (etc.远近mask)

主要了解视线向量，法线，光向量

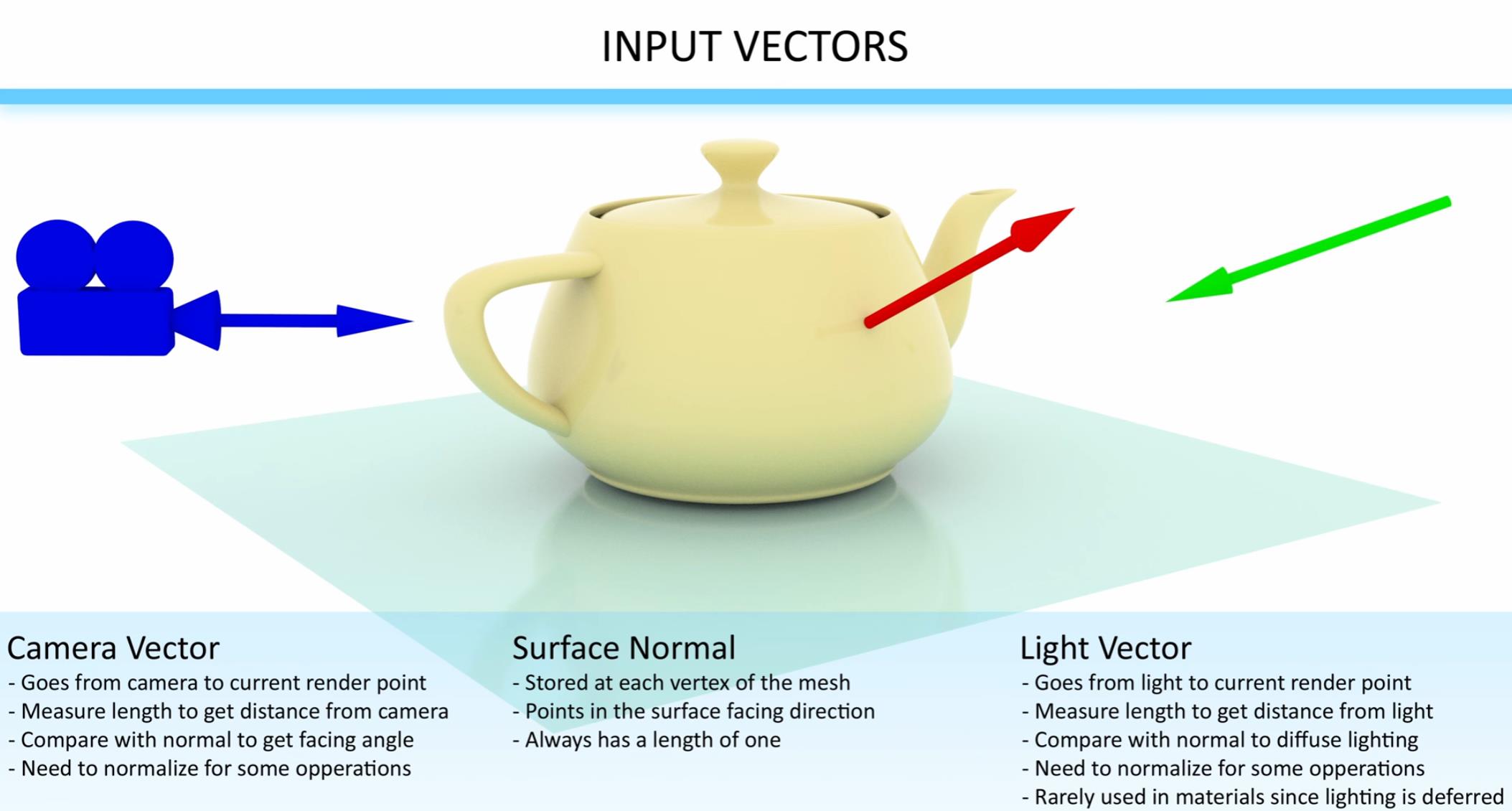
展示一些向量的用法，法线向上遮罩

NdotV简单的菲涅尔

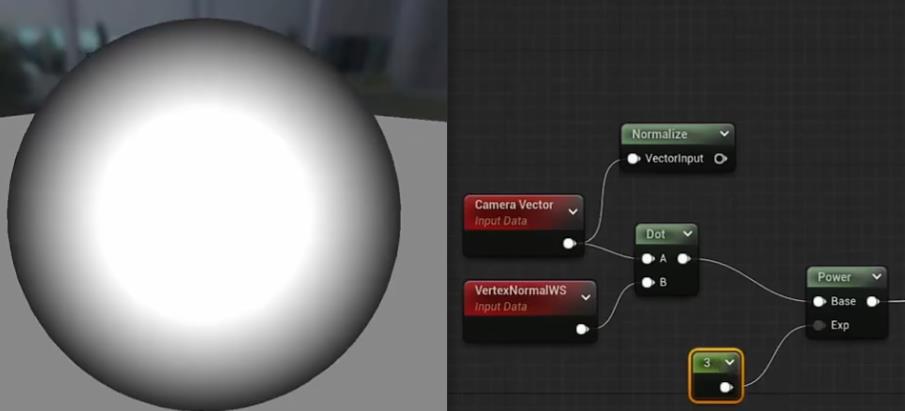
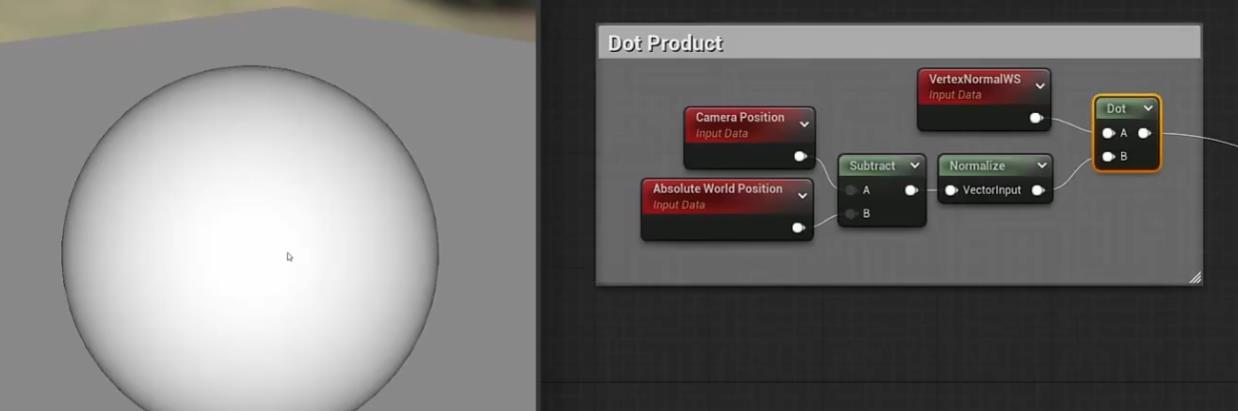
计算相机向量，根据相机远近进行明暗变化

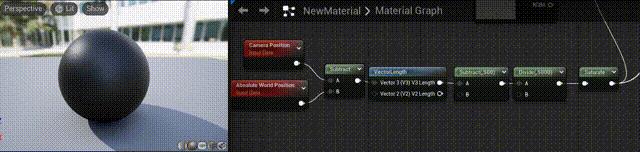
Lec10 View, World, Object, & Tangent Space 坐标空间 (etc.matcap,法线混合)

基本概念，可参考
LearnOpenGL学习笔记—入门07：Coordinate Systems

案例 将法线转入view space实现matcap
MatCap原理介绍及应用

案例 将法线从tangent space转入world space实现环境材质混合，如果想直接在模型顶部混合则转入local space就可以
UE4 Material 101学习笔记——01-07 介绍/PBR基础/UV扭曲/数据类型/翻页动画/材质混合/性能优化

Lec11 Min Max Clamp Saturate 最大最小钳制饱和

四个节点都用于限制数据范围
min 接受两个值输出小值
max 接受两个值输出大值
clamp 将值钳制在某范围
saturate 将值钳制在0~1

Lec12 Blending Normal Maps 法线贴图混合方法

注：该节有一个很好的学习资料，详细描述了多种法线混合方法 ——Blending in Detail

首先需要注意UE(左)和Unity(右)的法线G通道是翻转的

UE类似于从底部被点亮，Unity类似从顶部被点亮

法线贴图不像其他贴图，法线贴图中的每个像素都代表着方向向量，所以混合方式也有所不同
法线贴图案例

第一种简单的方法，取RG两个通道相加，第三个通道用1，不过这种做法会略微削减法线的力量感，但是比较节省性能，这种方法可以对于水面，雨水波纹等不怎么要求法线准确的效果

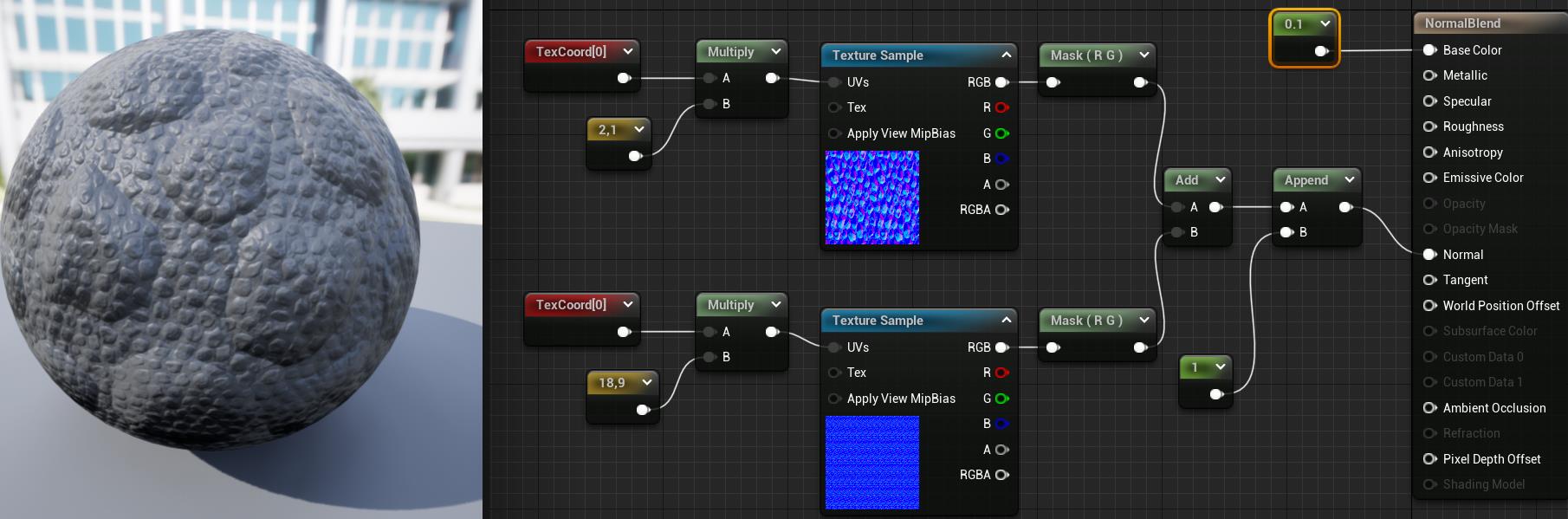
第二种是UDN方法，取第一张图的Z，会更准确，性能会比第一种消耗高一点

第三种是WhiteOut方法，这个名字是因为在AMD的Ruby : Whiteout演示中使用过，将Z通道乘起来，这样detail normal也会更明显，质量更好，但性能上消耗又更高一点

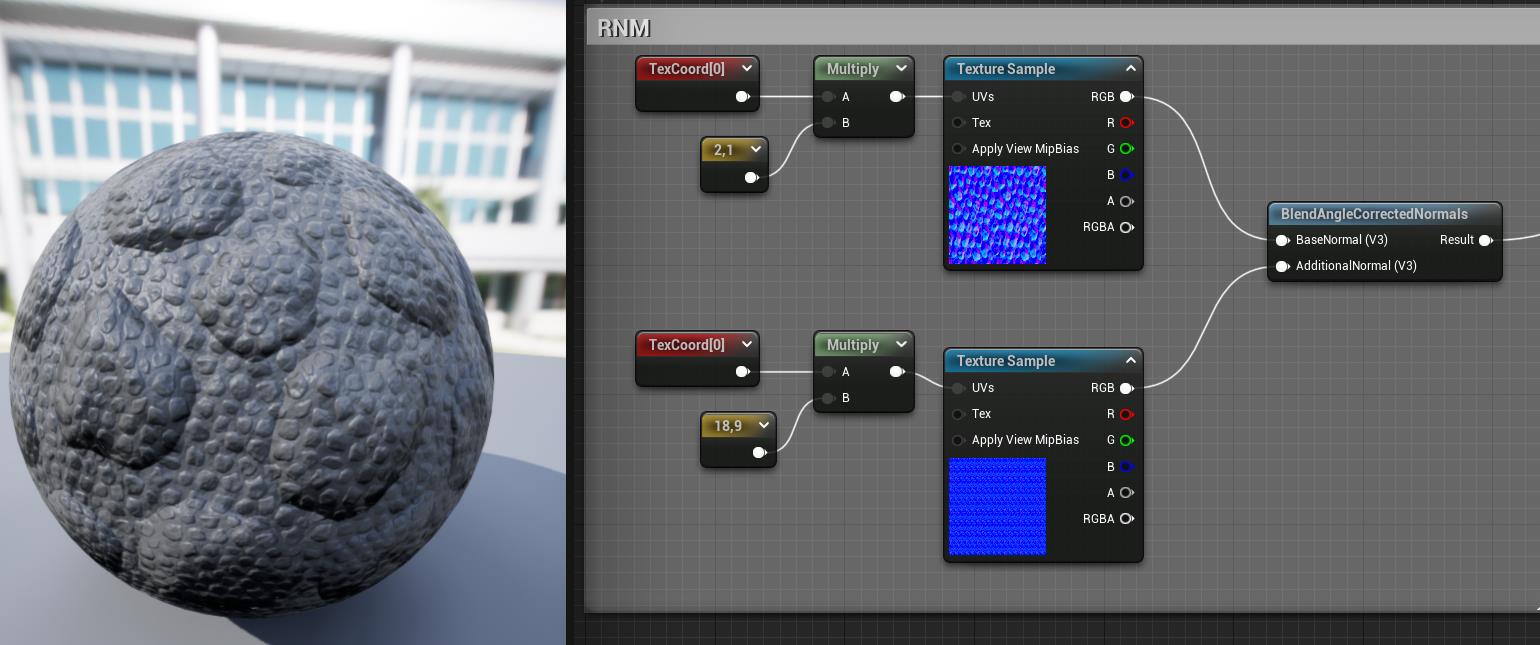
第四种是RNM方法，比较复杂但也是最精确的，也是UE自带的BlendAngleCorrectedNormals内使用的方法，和第三种差不多，效果上可能会好一些