ecjtuacm2022 C-n层妖塔

Posted 2022-12-10 帅气的黑桃J

Description

链接：https://ac.nowcoder.com/acm/contest/44482/C
来源：牛客网

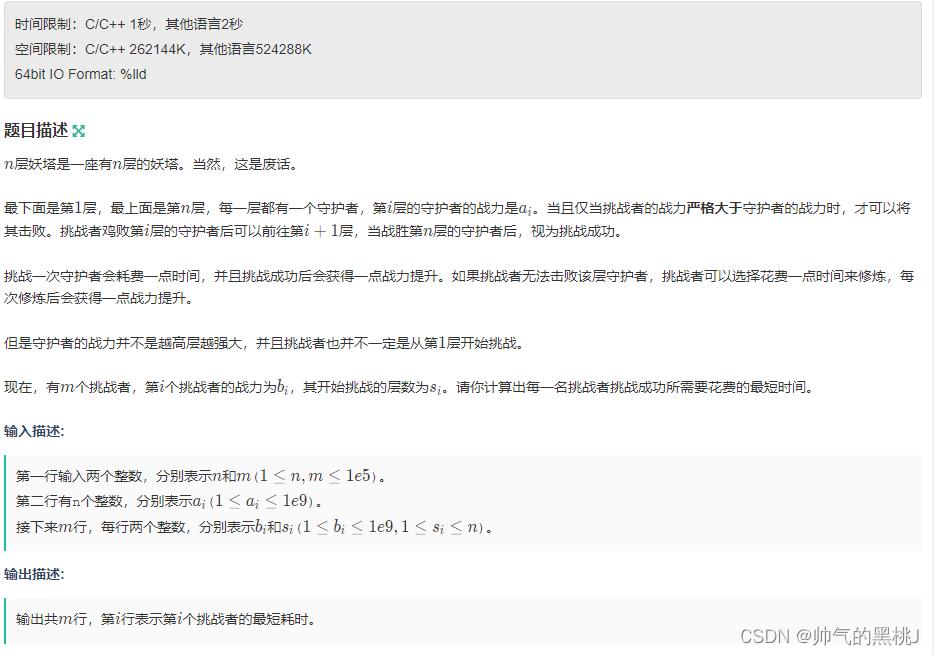
n层妖塔是一座有n层的妖塔。当然，这是废话。

最下面是第11层，最上面是第nn层，每一层都有一个守护者，第ii层的守护者的战力是a_ia  。当且仅当挑战者的战力严格大于守护者的战力时，才可以将其击败。挑战者鸡败第ii层的守护者后可以前往第i+1i+1层，当战胜第nn层的守护者后，视为挑战成功。

挑战一次守护者会耗费一点时间，并且挑战成功后会获得一点战力提升。如果挑战者无法击败该层守护者，挑战者可以选择花费一点时间来修炼，每次修炼后会获得一点战力提升。

但是守护者的战力并不是越高层越强大，并且挑战者也并不一定是从第11层开始挑战。

现在，有mm个挑战者，第ii个挑战者的战力为b_ib  ，其开始挑战的层数为s_is 

​请你计算出每一名挑战者挑战成功所需要花费的最短时间。

Demo1

input

5 2
1 3 3 7 5
2 1
1 2

output

8
9

说明

对于第一个战力为2从第一层开始的挑战者：
花费1点时间击败第一层，战力变为3。
由于无法击败第二层，所以花费1点时间修炼，战力变为4。花费1点时间击败第二层，战力变为5。
花费1点时间击败第三层，战力变为6。
由于无法击败第四层，花费2点时间修炼，战力变为8。花费1点时间击败第四层，战力变为9。
花费1点时间击败第五层，战力变为10。
共花费了8点时间。

Demo2

input

6 5
1 1 4 5 1 4
1 1
2 1
1 3
2 4
5 4

output

8
7
8
7
4

Analysis

萌新，看到这题直接暴力走了一遍常规思路，按照题意模拟了一遍如下：

n, m = list(map(int, input().split()))
a_arr = list(map(int, input().split()))
b_arr = []
for i in range(m):
    # [战力,开始层数]
    b_arr.append(list(map(int, input().split())))
    ori_power = b_arr[i][0]

    # npc: j层数, a_arr[j]战力
    for j in range(b_arr[i][1] - 1, len(a_arr)):
        if b_arr[i][0] > a_arr[j]:
            b_arr[i][0] += 1
        else:
            b_arr[i][0] += a_arr[j] - b_arr[i][0] + 1

    print(b_arr[i][0] - ori_power + 1)

结果嘿嘿，直接超时，复杂度n^2了，笨方法，方法2如下：

"""
假设当前需要从第 层开始挑战，考虑战力至少为多少时，才能恰好不受阻碍（指不需要中途修炼）的挑战成
功。假设该临界战力是 ，那么挑战者的战力如果大于等于 ，那么直接一路平推过去即可。如果战力小于 ，我
们不妨在挑战之前，先把战力修炼到 ，然后在出发挑战。否则，我们一定会在挑战某一层的时候需要修炼。而
我们只是将所有的中途修炼改为了提前修炼。
我们定义f[i]表示从第 层开始挑战，战力至少为多少，才能不受阻碍的挑战成功。显然我们需要提前预处理出来
这个f数组。其可以使用递推的方式进行求解。递推方程为f[i] = max(a[i] + 1, f[i+1] - 1)
时间复杂度O(m+n)
"""

n, m = map(int, input().split())
f = list(map(int, input().split()))
f.insert(0, 0)
f[n] += 1

for i in range(n - 1, 0, -1):
    f[i] = max(f[i] + 1, f[i+1] - 1)
print(f)
for i in range(m):
    b, s = list(map(int, input().split()))

    if b >= f[s]:
        print(n - s + 1)
    else:
        print(f[s] - b + n - s + 1)

方法二递推了一遍，快多了，复杂度O(m+n)。