深度学习实战案例：电影评论二分类

Posted 2022-12-08 尤尔小屋的猫

第一个深度学习实战案例：电影评论分类

公众号：机器学习杂货店
作者：Peter
编辑：Peter

大家好，我是Peter~

这里是机器学习杂货店 Machine Learning Grocery~

本文的案例讲解的是机器学习中一个重要问题：分类问题。

本文是《Python深度学习》一书中的实战案例：电影评论的二分类问题。

训练集和测试集

这是一个典型的二分类问题。使用的是IMDB数据集，训练集是25000条，测试也是25000条

In [1]:

import pandas as pd
import numpy as np

from keras.datasets import imdb

In [2]:

# 10000：仅保留训练数据中前10000个最常见的词语

(train_data, train_labels),(test_data, test_labels) = imdb.load_data(num_words=10000)

• train_data、test_data：评论组成的列表
• train_labels、test_lables：0-1组成的列表。其中0-负面 1-正面

In [3]:

train_data.shape

Out[3]:

(25000,)

In [4]:

type(train_data)

Out[4]:

numpy.ndarray

In [5]:

# train_data[3]

In [6]:

test_labels[1]  # 标签值都是0或者1

Out[6]:

1

单词的最大索引不超过10000：

In [7]:

# [max(i) for i in train_data]：每组数据的

max([max(i) for i in train_data])

Out[7]:

9999

数据还原

将数值还原到对应的评论中

In [8]:

# 步骤1：单词和数值组成的字典

word_index = imdb.get_word_index()

In [9]:

# 步骤2: key-value翻转
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
reverse_word_index

准备数据

不能将整数序列直接输入到神经网络，必须先转成张量；提供两种转换方法：

• 填充列表，使其具有相同的长度，再将列表转成(samples,word_indices)的整数张量；再使用Embedding层进行处理（后续介绍）
• 对列表进行one-hot编码，转成0-1组成的向量。网络第一层可以Dense层，处理浮点数向量数据

one-hot编码

In [10]:

# one-hot编码实现

import numpy as np

def vectorize_sequences(sequences, dimension=10000):
    results = np.zeros((len(sequences), dimension)) # 创建全0矩阵
    
    for i, sequence in enumerate(sequences):  
        results[i, sequence] = 1.  # 指定位置填充1
    return results

# 训练数据和测试数据向量化
x_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)

In [11]:

x_train[0]

Out[11]:

array([0., 1., 1., ..., 0., 0., 0.])

标签向量化

In [12]:

y_train = np.asarray(train_labels).astype("float32")
y_test = np.asarray(test_labels).astype("float32")

构建神经网络

输入数据是向量，标签是标量（0或者1）。在该类问题上表现好的神经网络：带有relu激活函数的全连接Dense层网络

Dense(16,activation='relu')

• 16：表示隐藏单元的个数；一个隐藏单元表示空间的一个维度
• 每层都对应一个表示空间，数据经过层层变换，最终映射到解

中间层使用relu函数作为激活函数，使用的主要运算：

output = relu(dot(W,input) + b)

最后一层使用sigmod激活，输出一个0-1之间的概率值作为样本的目标值等于1的可能性，即正面的可能性

1. relu函数：将全部负值归0
2. sigmoid函数：将数据压缩到0-1之间

模型定义（修改）

In [13]:

import tensorflow as tf  # add
import keras as models
import keras as layers

model = models.Sequential()

# 原文model.add(layers.Dense(16, activation="relu", input_shape=(10000, )))

# 统一修改3处内容：layers.Dense 变成 tf.keras.layers.Dense

# 输入层
model.add(tf.keras.layers.Dense(16,
                      activation="relu",
                      input_shape=(10000, )))
# 隐藏层1
model.add(tf.keras.layers.Dense(16,
                       activation="relu"))
# 隐藏层2
model.add(tf.keras.layers.Dense(1,
                      activation="sigmoid"))

损失函数和优化器（修改）

这个问题属于二分类问题，网络输出的是一个概率值。

最后一层使用sigmoid函数作为激活函数，最好使用binary_crossentropy（二元交叉熵）作为损失。

温馨提示：对于输出是概率值的模型，最好使用交叉熵crossentropy（用于衡量概率值分布之间的距离）。

下面的优化过程是使用：

• 优化器：rmsprop
• 损失函数：binary_crossentropy

In [14]:

# 编译模型
model.compile(optimizer="rmsprop",  # 优化器
              loss="binary_crossentropy",  # 损失
              metrics=["accuracy"]  # 指标函数
             )

自定义优化器、损失函数、指标函数等：

In [15]:

# 配置优化器

from keras import optimizers

# 原文：optimizer = optimizers.RMSprop(lr=0.001)
# 修改地方：optimizers --->  tf.keras.optimizers
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=0.001),
             loss="binary_crossentropy",
             metrics=["accuracy"]
             )

In [16]:

# 自定义损失函数和指标

from keras import losses 
from keras import metrics

# 原文：optimizer = optimizers.RMSprop(lr=0.001)
# 修改地方：optimizers --->  tf.keras.optimizers

model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=0.001),
             loss=losses.binary_crossentropy,  # 自定义损失
              metrics=[metrics.binary_accuracy]  # 自定义指标函数
             )

验证模型

在原始训练数据集中留出10000个样本作为验证集

In [17]:

# 留出验证集

x_val = x_train[:10000]
partial_x_train = x_train[10000:]

y_val = y_train[:10000]
partial_y_train = y_train[10000:]

分批次进行迭代：

• 使用512个样本组成小批量
• 10000个样本将模型训练20次

同时监控模型在10000个样本上精度和损失

训练模型

In [18]:

model.compile(optimizer="rmsprop",
             loss="binary_crossentropy",
             metrics=["acc"])  # 使用acc作为评判指标

history = model.fit(partial_x_train, # 验证集
                   partial_y_train, 
                   epochs=20, # 批次
                   batch_size=512,  # 每个批次的样本数
                   validation_data=[x_val,y_val]  # 验证数据
                   )
Epoch 1/20
30/30 [==============================] - 5s 142ms/step - loss: 0.5198 - acc: 0.7864 - val_loss: 0.4005 - val_acc: 0.8677
Epoch 2/20
30/30 [==============================] - 1s 31ms/step - loss: 0.3109 - acc: 0.9039 - val_loss: 0.3070 - val_acc: 0.8853
Epoch 3/20
30/30 [==============================] - 1s 31ms/step - loss: 0.2274 - acc: 0.9269 - val_loss: 0.2794 - val_acc: 0.8893
Epoch 4/20
30/30 [==============================] - 1s 33ms/step - loss: 0.1799 - acc: 0.9411 - val_loss: 0.2829 - val_acc: 0.8854
Epoch 5/20
30/30 [==============================] - 1s 32ms/step - loss: 0.1452 - acc: 0.9542 - val_loss: 0.2846 - val_acc: 0.8867
Epoch 6/20
30/30 [==============================] - 1s 32ms/step - loss: 0.1209 - acc: 0.9619 - val_loss: 0.3057 - val_acc: 0.8825
Epoch 7/20
30/30 [==============================] - 1s 34ms/step - loss: 0.1001 - acc: 0.9693 - val_loss: 0.3122 - val_acc: 0.8826
Epoch 8/20
30/30 [==============================] - 1s 36ms/step - loss: 0.0818 - acc: 0.9767 - val_loss: 0.3412 - val_acc: 0.8807
Epoch 9/20
30/30 [==============================] - 1s 32ms/step - loss: 0.0661 - acc: 0.9821 - val_loss: 0.3739 - val_acc: 0.8741
Epoch 10/20
30/30 [==============================] - 1s 31ms/step - loss: 0.0564 - acc: 0.9857 - val_loss: 0.3854 - val_acc: 0.8750
Epoch 11/20
30/30 [==============================] - 1s 31ms/step - loss: 0.0442 - acc: 0.9896 - val_loss: 0.4420 - val_acc: 0.8675
Epoch 12/20
30/30 [==============================] - 1s 31ms/step - loss: 0.0352 - acc: 0.9926 - val_loss: 0.4520 - val_acc: 0.8722
Epoch 13/20
30/30 [==============================] - 1s 32ms/step - loss: 0.0307 - acc: 0.9935 - val_loss: 0.4773 - val_acc: 0.8714
Epoch 14/20
30/30 [==============================] - 1s 32ms/step - loss: 0.0220 - acc: 0.9971 - val_loss: 0.5152 - val_acc: 0.8688
Epoch 15/20
30/30 [==============================] - 1s 30ms/step - loss: 0.0190 - acc: 0.9968 - val_loss: 0.5547 - val_acc: 0.8677
Epoch 16/20
30/30 [==============================] - 1s 33ms/step - loss: 0.0160 - acc: 0.9974 - val_loss: 0.5821 - val_acc: 0.8684
Epoch 17/20
30/30 [==============================] - 1s 34ms/step - loss: 0.0090 - acc: 0.9994 - val_loss: 0.6170 - val_acc: 0.8668
Epoch 18/20
30/30 [==============================] - 1s 32ms/step - loss: 0.0098 - acc: 0.9985 - val_loss: 0.6487 - val_acc: 0.8658
Epoch 19/20
30/30 [==============================] - 1s 32ms/step - loss: 0.0091 - acc: 0.9985 - val_loss: 0.6858 - val_acc: 0.8648
Epoch 20/20
30/30 [==============================] - 1s 26ms/step - loss: 0.0041 - acc: 0.9999 - val_loss: 0.7136 - val_acc: 0.8661

调用模型model.fit方法会返回一个history对象。这个对象有一个history成员，它是一个字典，包含训练过程中的所有数据：

In [19]:

history_dict = history.history
history_dict

查看不同的key

In [20]:

history_dict.keys()  # 训练过程和验证过程的两组指标

Out[20]:

dict_keys(['loss', 'acc', 'val_loss', 'val_acc'])

绘图可视化

In [25]:

# 损失绘图
import matplotlib.pyplot as plt

history_dict = history.history
loss_values = history_dict["loss"]
val_loss_values = history_dict["val_loss"]

epochs = range(1,len(loss_values) + 1)  

# 训练
plt.plot(epochs,  #  横坐标
         loss_values,  # 纵坐标
         "r",  # 颜色和形状，默认是实线
         label="Training_Loss"  # 标签名
        )
# 验证
plt.plot(epochs,
         val_loss_values,
         "b",
         label="Validation_Loss"
        )

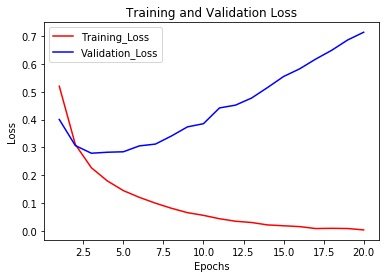
plt.title("Training and Validation Loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend()

plt.show()

# 精度绘图
import matplotlib.pyplot as plt

history_dict = history.history
acc_values = history_dict["acc"]
val_acc_values = history_dict["val_acc"]

epochs = range(1,len(loss_values) + 1)


plt.plot(epochs,
         acc_values,
         "r",
         label="Training_ACC"
        )

plt.plot(epochs,
         val_acc_values,
         "b",
         label="Validation_ACC"
        )

plt.title("Training and Validation ACC")
plt.xlabel("Epochs")
plt.ylabel("acc")
plt.legend()

plt.show()

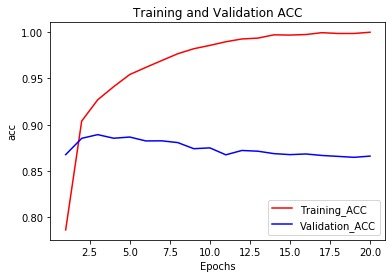
结论：

1. 训练的损失每轮都在降低；训练的精度每轮都在提升（红色）
2. 验证集的损失和精度似乎都在第4轮达到最优值

也就是：模型在训练集上表现良好，但是在验证集上表现的不好，这种现象就是过拟合

重新训练模型

通过上面的观察，第四轮的效果是比较好的：

In [23]:

import tensorflow as tf  # add
import keras as models
import keras as layers

model = models.Sequential()

# 原文model.add(layers.Dense(16, activation="relu", input_shape=(10000, )))
# 统一修改3处内容：layers.Dense 变成 tf.keras.layers.Dense

# 输入层
model.add(tf.keras.layers.Dense(16,
                      activation="relu",
                      input_shape=(10000, )))
# 隐藏层1
model.add(tf.keras.layers.Dense(16,
                       activation="relu"))
# 隐藏层2
model.add(tf.keras.layers.Dense(1,
                      activation="sigmoid"))


# 编译模型
model.compile(optimizer="rmsprop",
               loss="binary_crossentropy",
               metrics=["accuracy"]
              )

# fit过程
model.fit(x_train,y_train,
          epochs=4,   # 修改了这里，改成只循环4次
          batch_size=512
         )
# 模型评价
results = model.evaluate(x_test, y_test)
results
Epoch 1/4
49/49 [==============================] - 3s 29ms/step - loss: 0.4518 - accuracy: 0.8211
Epoch 2/4
49/49 [==============================] - 1s 23ms/step - loss: 0.2593 - accuracy: 0.9100
Epoch 3/4
49/49 [==============================] - 1s 22ms/step - loss: 0.1992 - accuracy: 0.9298
Epoch 4/4
49/49 [==============================] - 1s 26ms/step - loss: 0.1669 - accuracy: 0.9412
782/782 [==============================] - 4s 5ms/step - loss: 0.3053 - accuracy: 0.8800

Out[23]:

[0.30533847212791443, 0.8800399899482727]

可以看到在这种最简单的方法下，精度居然达到了88.54%！ 奈斯~

对测试集进行预测

训练好的网络对测试集进行预测：

In [24]:

model.predict(x_test)

Out[24]:

array([[0.23233771],
       [0.99984634],
       [0.94041836],
       ...,
       [0.17830989],
       [0.10676837],
       [0.7466589 ]], dtype=float32)

模型对某些样本的预测结果还是可信的，比如0.999和0.10等，有些效果不理想：出现0.56的概率值，导致无法判断

进一步实验

• 前面的案例使用的是两个隐藏层：可以尝试使用1个或者3个
• 尝试使用更多或更少的隐藏单元，比如32或者64个
• 尝试使用mse损失函数代替binary_crossentropy
• 尝试使用tanh函数（早期流行的激活函数）代替relu激活函数

小结

1. 对原始数据进行大量地预处理工作
2. 带有relu激活函数的Dense堆叠层，可以解决多种问题（包含情感分类）
3. 对于二分类问题：
   • 网络的最后一层使用带有sigmoid激活的Dense层，输出是0-1之间的概率值；
   • 同时建议使用binary_crossentropy作为损失函数
4. 优化器的最佳选择：rmsprop
5. 过拟合现象是常见的，因此一定要监控模型在训练数据集之外的数据集上的性能