sklearn基础篇-- 决策树（decision tree）

Posted 2022-12-08 长路漫漫2021

        决策树是广泛用于分类和回归任务的模型。本质上，它从一层层的if/else问题中进行学习，并得出结论。决策树学习算法包括3部分：特征选择、树的生成和树的剪枝。常用的算法有ID3、C4.5和CART。

        想象一下，你想要区分下面这四种动物：熊、鹰、企鹅和海豚。你的目标是通过提出尽可能少的if/else 问题来得到正确答案。你可能首先会问：这种动物有没有羽毛，这个问题会将可能的动物减少到只有两种。如果答案是“有”，你可以问下一个问题，帮你区分鹰和企鹅。例如，你可以问这种动物会不会飞。如果这种动物没有羽毛，那么可能是海豚或熊，所以你需要问一个问题来区分这两种动物——比如问这种动物有没有鳍。这一系列问题可以表示为一棵决策树，如下图所示。

import mglearn
import os
from graphviz import Digraph

# os.environ["PATH"] += os.pathsep + 'C:/Program Files/Graphviz/bin'

mglearn.plots.plot_animal_tree()

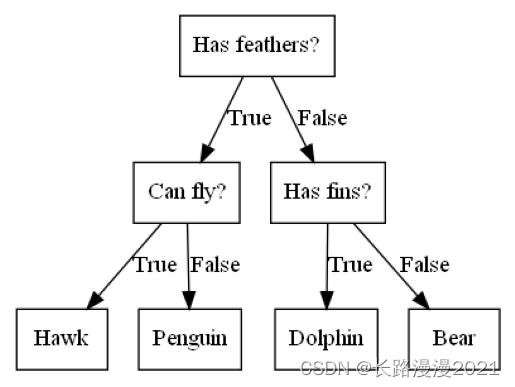图1 区分几种动物的决策树

        既然要做决策，需要决定的就是从哪个维度（特征）来做决策，例如前面例子中的会不会飞、有没有羽毛等。在机器学习中我们需要一个量化的指标来确定使用的特征更加合适，即使用该特征划分后，得到的子集合的“纯度”更高。这时引入三种指标——信息增益（Information Gain）、基尼指数（Gini Index）、均方差（MSE）来解决前面说的问题。

1 量化指标

1.1 信息熵

        熵度量了事物的不确定性，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下：
$$H(p)=H(X)=-\sum _{i=1}^n{p}_i\log p_i$$

        注意：熵只与$X$的分布有关，与$X$取值无关。定义$0\log 0=0$，熵是非负的。

1.2 条件熵

        随机变量$(X,Y)$的联合概率分布为

$P(X=x_i,Y=y_j)=p_{ij},i=1,2,\dots ,n;j=1,2,\dots ,m$

        两个变量$X$和$Y$的联合熵表达式如下：
$$H(X,Y)=-\sum _{x_i\in X}\sum _{y_i\in Y}p(x_i,y_i)logp(x_i,y_i)$$

        条件熵$H(Y|X)$表示在已知随机变量$X$的条件下随机变量$Y$的不确定性，类似于条件概率，它度量了在Y知道X以后剩下的不确定性。表达式如下：
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$
        其中$p_i=P(X=x_i),i=1,2,\dots ,n$

        $H(X)$度量了$X$的不确定性，条件熵$H(X|Y)$度量了我们在知道$Y$以后$X$剩下的不确定性，那么$H(X)-H(X|Y)$呢？从上面的描述大家可以看出，它度量了X在知道Y以后不确定性减少程度，这个度量我们在信息论中称为互信息，记为$I(X,Y)$。在决策树ID3算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大，则越适合用来分类。

        当熵和条件熵中的概率由数据估计(特别是极大似然估计)得到时，所对应的熵与条件熵分别称为经验熵和经验条件熵。就是从已知的数据计算得到的结果。

1.3 信息增益

        特征$A$对训练数据集$D$的信息增益$g(D|A)$，定义为集合$D$的经验熵$H(D)$与特征$A$给定的条件下$D$的经验条件熵$H(D|A)$之差
$$g(D,A)=H(D)-H(D|A)$$

        熵与条件熵的差称为互信息。决策树中的信息增益等价于训练数据集中的类与特征的互信息。

        考虑ID这种特征，本身是唯一的。按照ID做划分，得到的经验条件熵为0，会得到最大的信息增益。所以，按照信息增益的准则来选择特征，可能会倾向于取值比较多的特征。

那么，信息增益的物理意义是什么呢？
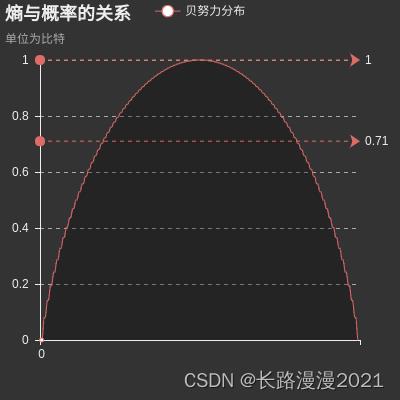
如果以概率$P(x)$为横坐标，以信息熵(Entropy)为纵坐标，把信息熵和概率的函数关系$Entropy=-P(x)lo{g}_{2}P(x)$在二维坐标系上画出来就可以看出(标有“Entropy”的曲线)，当概率$P(x)$越接近0或越接近1时，信息熵的值越小，其不确定性越小，即数据越“纯”。比如说当概率为1时，数据是最“纯净的”，已经消除了不确定性，其信息熵为0。我们在选择特征的时候，选择信息增益最大的特征，在物理意义上就是让数据尽量往更纯净的方向上变换。因此，信息增益是用来衡量数据变得更有序、更纯净的程度的指标。

1.4 信息增益比

        引入一个信息增益比的变量$g_R(D,A)$，它是信息增益和特征熵的比值。表达式如下：
$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}$$

        对于特征熵$H_A(D)$, 表达式如下：
$$H_A(D)=-\sum _{i=1}^n\frac{D_i}{D}lo{g}_2\frac{以上是关于sklearn基础篇--\; 决策树（decision\; tree）的主要内容，如果未能解决你的问题，请参考以下文章}{D}$$

Python_sklearn机器学习库学习笔记decision_tree（决策树）

机器学习-决策树 Decision Tree

Spark MLlib速成宝典模型篇05决策树Decision Tree（Python版）

SKLearn 包装器中 XGBoost 的决策函数

机器学习之决策树(Decision Tree)

Decision Tree 1: Basis 决策树基础