激活函数 Sigmoidtanh*LUsoftPlusmaxOutsoftmaxdice- 杂记

Posted 一杯敬朝阳一杯敬月光

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了激活函数 Sigmoidtanh*LUsoftPlusmaxOutsoftmaxdice- 杂记相关的知识，希望对你有一定的参考价值。

目录

1.Sigmoid

2. tanh

3.ReLU

4.Leaky Relu

5.PRelu

6.Elu

6.softPlus

7.大一统：maxOut

传统的激活函数选择的建议 

8.softmax

9.Dice

1.Sigmoid

，导数：

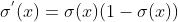
优点：平滑、易求导。可以将函数映射到(0, 1)之间，通常二分类算法会在最后套一层sigmoid函数。

缺点：

  • 计算量大，包含指数运算
  • Sigmoid导数取值范围是[0, 0.25]，当输入为5的时候梯度就已经很小了大概0.0067，即使梯度在0.25，每一层的反向传播都会使梯度最少变为原来的四分之一，神经网络层数多了，反向传播的时候（链式法则）梯度也会很小，例如10层神经网络0.25 ** 10 大概是9.5367431640625e-07，已经很小了，容易出现梯度消失的现象
  • 输出不是0均值 

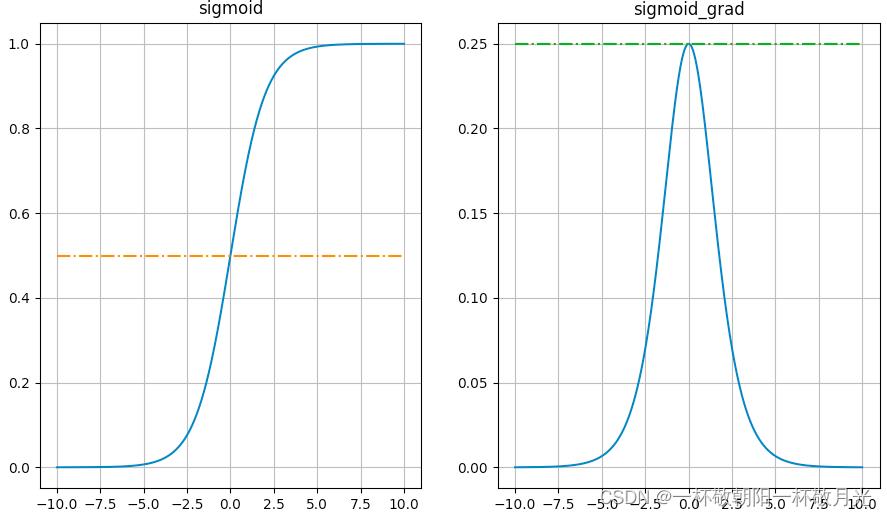
sigmoid函数做输出层的激活函数的时候，损失函数一般使用交叉熵损失。一是因为，sigmoid通常用于二分类，我们只要在并不要求输出一定等于标签，只要是正例的时候预测值高于0.5就行，负例的时候预测值小于0.5，用MSE过于严苛，交叉熵损失只关心对正确类别的预测概率。 二是因为因为若使用MSE，在模型刚开始训练的时候参数更新速度会比较慢，因为我们通常会用较小的值来初始化参数，那么输出值就会较小，MSE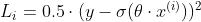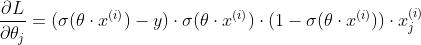：,，梯度包含sigmoid函数的导数，sigmoid的导数在值比较小的时候会接近0。而使用交叉熵损失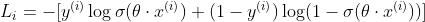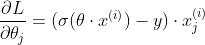，，,不存在这种现象。

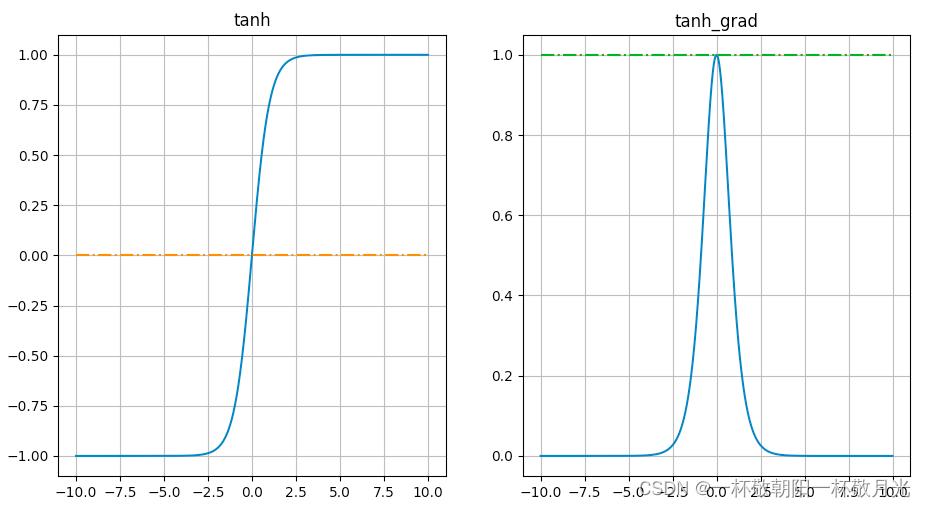
2. tanh

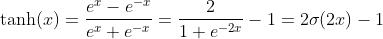，导数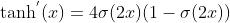

 优点：

  • 输出是0均值
  • 梯度取值范围在(0, 1)之间

缺点：

  • 同sigmoid一样，计算量大，包含指数运算
  • 从下图可以看出，尽管其梯度在(0, 1)之间，但是饱和区依旧很大，例如输入是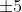的时候大概是0.00018

3.ReLU

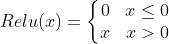，导数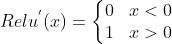

优点：

  • 计算简单
  • 收敛速度快，relu函数有助于随机梯度下降方法收敛，收敛速度大概比sigmoid和tanh快6倍左右。
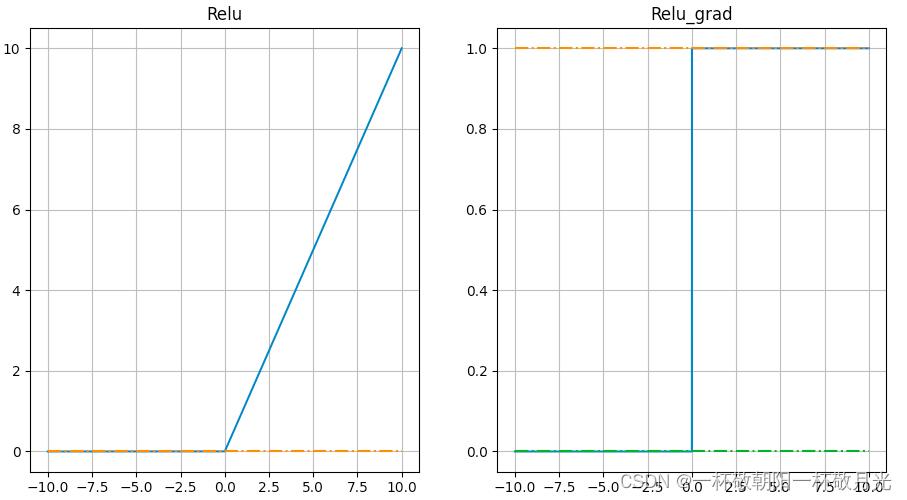
  • 在大于0的一半，不存在梯度饱和的现象

缺点：

  • 不是0均值
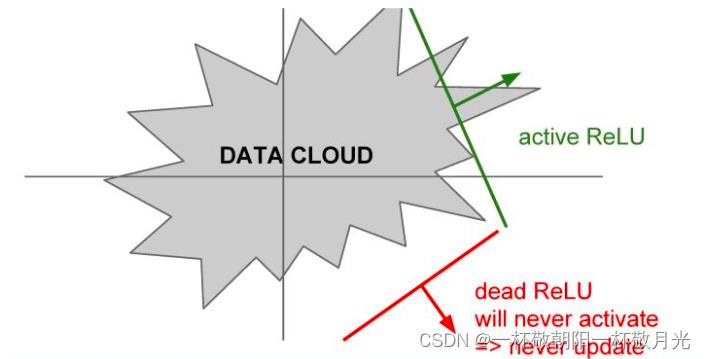
  • Dead ReLU Problem，这里不是很理解，直接各种抄抄，当在负半轴的区域中的时候，这里主要有几个可能的原因。如果观察数据云，假设这个就是全部的训练数据，可以看到这些ReLU可能处于的位置。这些RuLU基本上在平面中的一半区域能够产生激活，在这个平面区域内能够激活的又相应地定义了这些ReLU，可以看到这些dead ReLU基本不在数据云中，因此它从来不会被激活和更新，相比激活的ReLU，一些数据是正数，那么就能进行传递，一些则不会。主要有以下几个原因：第一是当有一个不好的初始化的时候，即权重设置非常的不好，它们恰巧不在数据云中，这就会出现dead ReLU的情况，这就导致不能得到一个激活神经元的数据输入，同时也不会有一个合适的梯度传回来，它不会被更新和激活。当学习率很大的时候，在这种情况下从一个ReLU函数开始，但因为在进行大量的更新，权重不断波动，然后ReLU单元会被数据的多样性所淘汰。这些会在训练时发生，它在开始阶段很正常，但在某个时间节点之后变差，最后挂掉。所以如果实际上你冻结了一个已经训练好的网络，然后将数据放进去，可以看到实际上网络中有10%到20%的部分是这些挂了的ReLU单元。大多数使用ReLU的网络都有这类问题，在实际运用中大家会深入检查ReLU单元。（cs231n课程笔记--激活函数 - 走看看），指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。（为什么ReLu激活函数要好于tanh和sigmoid?_导数）。在训练的时候，ReLU单元比较脆弱并且可能“死掉”。举例来说，当一个很大的梯度流过ReLU的神经元的时候，可能会导致梯度更新到一种特别的状态，在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生，那么从此所以流过这个神经元的梯度将都变成0。也就是说，这个ReLU单元在训练中将不可逆转的死亡，因为这导致了数据多样化的丢失。例如，如果学习率设置得太高，可能会发现网络中40%的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。通过合理设置学习率，这种情况的发生概率会降低。（cs231n神经网络 常用激活函数 - 喵喵帕斯 - 博客园）

4.Leaky Relu

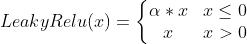 导数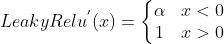

优点

  • 同relu
  • 小于0的半边没有梯度饱和的现象，不存在Dead ReLU Problem

缺点

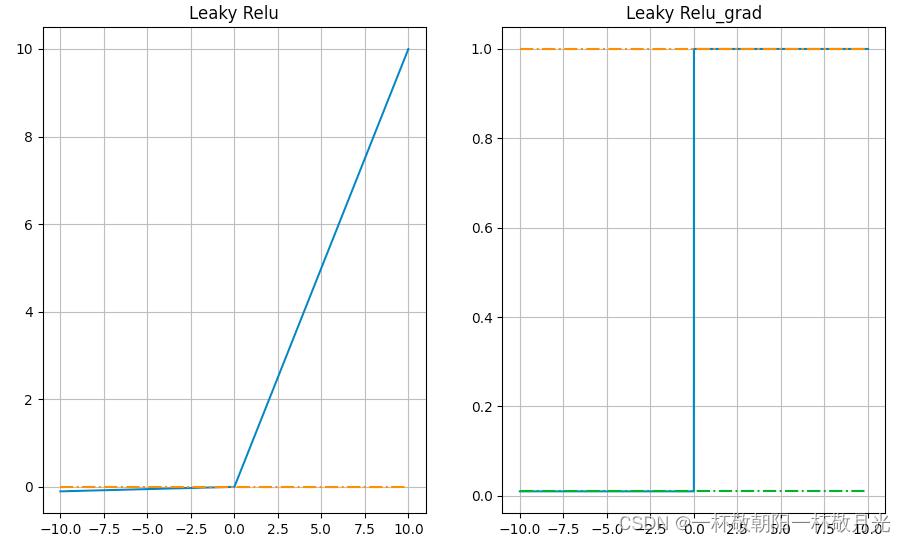
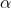  • 是超参，有博客说Leaky Relu对其敏感

5.PRelu

形式同leaky relu，区别在于PRelu的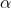不是超参，而是学习出来的。

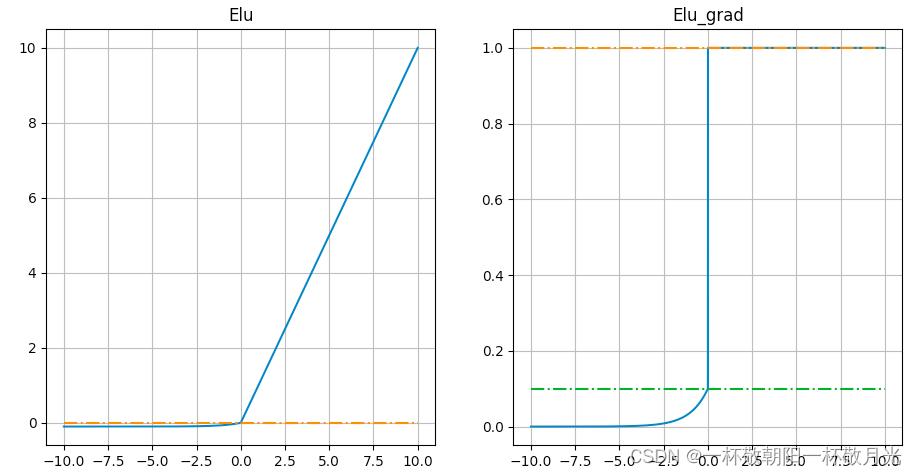
6.Elu

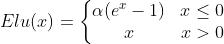，导数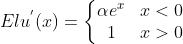

优点

  • 收敛速度快
  • 不会有Deal ReLU问题
  • 输出的均值接近0，zero-centered
  • 左侧软饱合能够让ELU对输入变化或噪声更鲁棒

缺点

  • 包含指数，计算量大

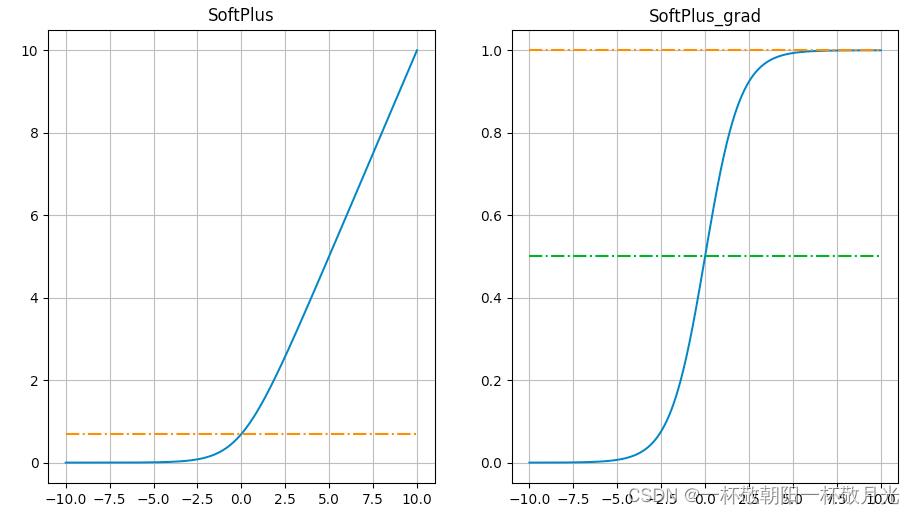
6.softPlus

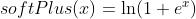，其导数就是sigmoid函数,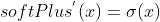 

值域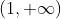：，可以看作是对Relu的平滑，当x比较大的时候，相对于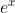来说1的影响很小了，再取对数就近似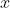了。

缺点

  1. 非0均值
  2. 包含指数，计算量大
  3. 当x取绝对值较大的负数时依旧会出现梯度近似0的情况
  4. 不具备relu的快速收敛

优点

  • 解决了dead relu的问题

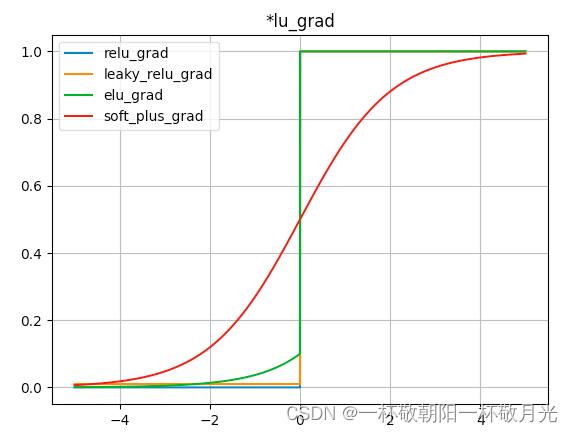
7.大一统：maxOut

 

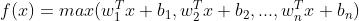
缺点就是参数量多，明显增加了计算量，使得应用maxout的层的参数个数成k倍增加，原本只需要1组就可以，采用maxout之后就需要k倍了。

传统的激活函数选择的建议 

  1. 优先relu
  2. 再考虑prelu、leaky relu、maxout
  3. 再考虑tanh
  4. 除非用作二分类的最后一层，其他一般不建议使用sigmoid

下图截自cs231n视频

8.softmax

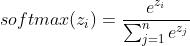
  • 值域0-1之间
  • 通常用于多分类的输出，所有分类的输出之和为1
  • 指数函数曲线呈现递增趋势，最重要的是斜率逐渐增大，也就是说在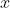轴上一个很小的变化，可以导致y轴上很大的变化。经过使用指数形式的Softmax函数能够将差距大的数值距离拉的更大。但是这样也有可能会产生溢出。
  • 使用Softmax函数作为输出层激活函数时，常使用交叉熵作损失函数。Softmax函数计算过程中，容易因为输出节点的输出值较大产生溢出现象，在计算交叉熵时也可能会产生溢出。为了计算的稳定性，TensorFlow提供了一个统一的接口，将Softmax与交叉熵损失函数同时实现，同时也处理了数值不稳定的异常，使用TensorFlow深度学习框架的时候，推荐使用这个统一的接口，避免分开使用Softmax函数与交叉熵损失函数。

softmax由于使用指数容易产生溢出，解决溢出的小trick，CS231n Convolutional Neural Networks for Visual Recognition

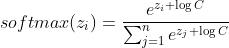 ，可以自由选择C，通常选择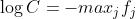，这样指数的最高幂次是0，整个指数不会超过1。

f = np.array([123, 456, 789]) # example with 3 classes and each having large scores
p = np.exp(f) / np.sum(np.exp(f)) # Bad: Numeric problem, potential blowup

# instead: first shift the values of f so that the highest number is 0:
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # safe to do, gives the correct answer

9.Dice

先mark一下，感觉讲的很赞，DIN笔记 - 知乎

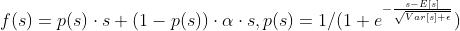
和Batch Normalization有异曲同工之妙，BN

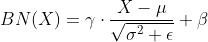
令BN的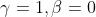，有

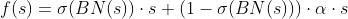
绘图代码： 

import numpy as np
from matplotlib import pyplot as plt


def grad(y, z, step):
    g = (y[1:] - y[:-1]) / step
    x = (z + step / 2.)[:-1]
    top = np.max(g)
    return x, g, top


def mySigmoid(z):
    return 1. / (1 + np.exp(-z))

def myTanh(z):
    return 2. / (1 + np.exp(-2.*z)) - 1
    # return (np.exp(z) - np.exp(-z)) / (np.exp(z) + np.exp(-z))
    # return 2 * mySigmoid(2 * z) - 1


def myRelu(z):
    return np.where(z <= 0, 0., z)


def myLeakyRelu(z):
    return np.where(z <= 0, 0.01 * z, z)


def myElu(z):
    alpha = 0.1
    return np.where(z <= 0, alpha * (np.exp(z) - 1), z)


def mySoftPlus(z):
    return np.log(1 + np.exp(z))


def myPlot(func, title):
    step = 0.0001
    start, end = -10, 10 + step
    num = (end - start) / step
    z = np.linspace(start, end, num)
    y = func(z)
    x, g, top = grad(y, z, step)

    plt.subplot(1, 2, 1)
    plt.plot(z, y)
    plt.plot(np.linspace(start, end, 10), [func(0)] * 10, '-.')
    plt.grid()
    plt.title(title, loc='center')
    plt.subplot(1, 2, 2)
    plt.plot(x, g)
    plt.plot(np.linspace(start, end, 10), [top] * 10, '-.')
    plt.plot(np.linspace(start, end, 10), [g[g.shape[0] // 2 - 2]] * 10, '-.')
    plt.grid()
    plt.title(title + '_grad', loc='center')
    plt.show()

# myPlot(mySigmoid, 'sigmoid')
myPlot(myTanh, 'tanh')
# myPlot(myRelu, 'Relu')
# myPlot(myLeakyRelu, 'Leaky Relu')
# myPlot(myElu, 'Elu')
# myPlot(mySoftPlus, 'SoftPlus')

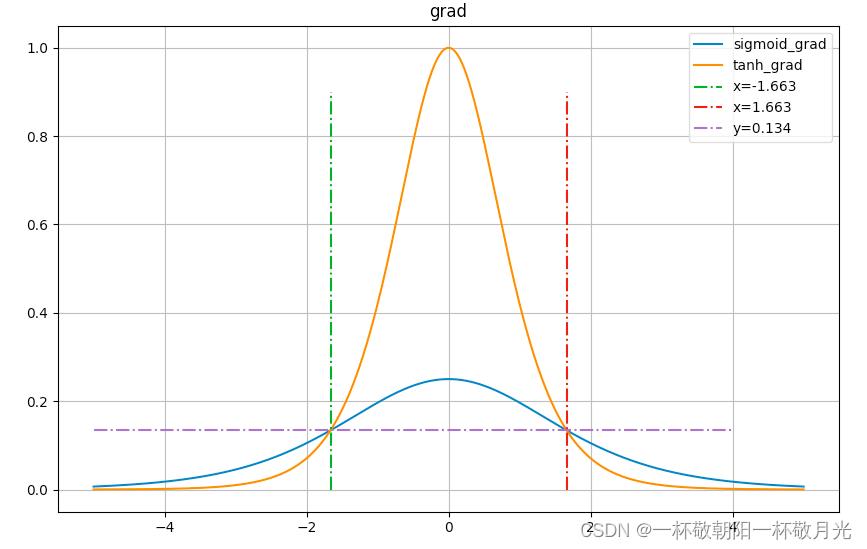
def sigmoid_tanh():
    step = 0.0001
    start, end = -5, 5 + step
    num = (end - start) / step
    z = np.linspace(start, end, num)
    y1 = mySigmoid(z)
    x1, g1, top1 = grad(y1, z, step)
    plt.plot(x1, g1, label='sigmoid_grad')

    y2 = myTanh(z)
    x2, g2, top2 = grad(y2, z, step)
    plt.plot(x2, g2, label='tanh_grad')

    i = 0
    for i in range(z.shape[0]):
        if g2[i] >= g1[i]:
            break
    plt.plot([z[i]] * 10, [0.1 * j for j in range(10)], '-.', label="x=".format(round(z[i],3)))

    for j in range(i + 2, z.shape[0]):
        if g2[j] <= g1[j]:
            break
    plt.plot([z[j]] * 10, [0.1 * k for k in range(10)], '-.', label="x=".format(round(z[j], 3)))
    plt.plot([k for k in range(-5, 5)], [g2[j]] * 10, '-.', label="y=".format(round(g2[j], 3)))

    plt.grid()
    plt.title('grad', loc='center')
    plt.legend()  #
    plt.show()

# sigmoid_tanh()


def all_lu():
    step = 0.0001
    start, end = -5, 5 + step
    num = (end - start) / step
    z = np.linspace(start, end, num)
    y1 = myRelu(z)
    x1, g1, top1 = grad(y1, z, step)
    plt.plot(x1, g1, label='relu_grad')

    y2 = myLeakyRelu(z)
    x2, g2, top2 = grad(y2, z, step)
    plt.plot(x2, g2, label='leaky_relu_grad')

    y3 = myElu(z)
    x3, g3, top3 = grad(y3, z, step)
    plt.plot(x3, g3, label='elu_grad')

    y4 = mySoftPlus(z)
    x4, g4, top4 = grad(y4, z, step)
    plt.plot(x4, g4, label='soft_plus_grad')

    plt.grid()
    plt.title('*lu_grad', loc='center')
    plt.legend()
    plt.show()

# all_lu()

以上是关于激活函数 Sigmoidtanh*LUsoftPlusmaxOutsoftmaxdice- 杂记的主要内容，如果未能解决你的问题，请参考以下文章

如何选择激活函数

CNN基础——激活函数

激活函数总结

激活函数

常用激活函数比较

激活函数总结