2021-3-27春季个人赛补题（B - Minimal Area（叉乘法求三角形面积））

Posted 2022-12-07 如风如影�

B - Minimal Area(叉乘法求三角形面积）

题目链接: link.
原题描述：
You are given a strictly convex polygon. Find the minimal possible area of non-degenerate triangle whose vertices are the vertices of the polygon.
The first line contains a single integer n (3 ≤ n ≤ 200000) — the number of polygon vertices.

Each of the next n lines contains two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — the coordinates of polygon vertices.

The polygon is guaranteed to be strictly convex. Vertices are given in the counterclockwise order.
It is known that the area of triangle whose vertices are the integer points on the grid is either integer or half-integer.

Output a single integer — the required area, multiplied by 2.

题意：

：按逆时针的顺序给出一个凸多边形的n个顶点，求一个顶点都在凸多边形上，面积最小的三角形，输出三角形面积的二倍

思路
面积最小的三角形一定是三个相连的顶点的面积，按顺序遍历每三个相连的顶点，找最小值.

已知三点坐标，求构成的三角形面积，这就用到了叉乘公式，推理过程如下：


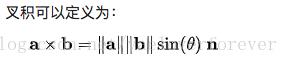
因此，叉乘法求三角形面积公式为：abs((x2y3-x3y2)-(x1y3-x3y1)+(x1y2-x2y1)),合并一下即为abs((x2-x1)(y3-y1)-(y2-y1)(x3-x1))

代码如下

#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
struct node 
    long double x, y;
 a[N];
long long s(node a, node b, node c) 
    long long x1 = a.x;
    long long x2 = b.x;
    long long x3 = c.x;
    long long y1 = a.y;
    long long y2 = b.y;
    long long y3 = c.y;
    long long sum1 = x2 * y3 - x3 * y2;
    long long sum2 = x1 * y3 - x3 * y1;
    long long sum3 = x1 * y2 - x2 * y1;
    return abs(sum1 - sum2 + sum3);

int main() 
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) 
        cin >> a[i].x >> a[i].y;
    
    a[n + 1] = a[1];//类似于约瑟夫环遍历方法，因为下面是从i=3开始的。
    a[n + 2] = a[2];
    n = n + 2;
    long long int m = 0x3f3f3f3f3f3f3f3f;
    for (int i = 3; i <= n; i++) 
        long long int f = s(a[i], a[i - 1], a[i - 2]);
        m = min(m, f);
    
    cout << m << endl;
    return 0;