时滞微分方程求解之三ddesd--变时滞

Posted 2022-12-07 studyer_domi

参考：

绘制含有时滞的微分方程组的曲线图像的matlab程序 – MATLAB中文论坛

ddesd说明：具有状态依赖时滞的 DDE- MATLAB & Simulink- MathWorks 中国

考虑下面的变时滞微分方程

 

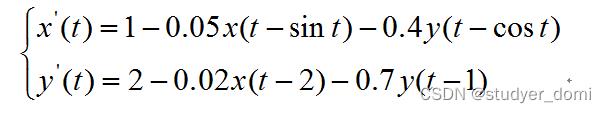
试绘制上述含有时变时滞微分方程的图像

分析：该方程应该在某个t0时间之后成立，初始值必须是定义在t0之前的一个关于t的单值向量函数phi(t)。

我假设t0=0吧，phi(t)=[1;-1];

matlab程序：

function ddeex
t0 = 0;
tfinal = 5;
tspan = [t0, tfinal];
sol = ddesd(@ddefun,@delay,@hist,tspan);
plot(sol.x,sol.y,'.-')
xlabel('time')
ylabel('value')
legend('x','y')

function d=delay(t,y)
  d=[t-sin(t);t-cos(t);t-2;t-1];


function h=hist(t)
  h=[1;-1];


function dydt = ddefun(t,y,Z)   
  dydt = [1-0.05*Z(1,1)-0.04*Z(2,2); 2-0.02*Z(1,3)-0.7*Z(2,4)];

图像如下