如何求联合分布函数和边缘分布函数?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了如何求联合分布函数和边缘分布函数?相关的知识,希望对你有一定的参考价值。
参考技术A对已知的联合分布函数求二次偏导数,也就是求出联合密度函数。然后根据你需要求出边缘分布函数的那个随机变量进行相应的二重积分,得出答案。如Fx(x)=∫-∝→x[∫-∝→+∝f(x,y)dy]dx
当一个确定的正弦信号,经过随机起伏信道传输后,到达接收点时其振幅、相位和角频率已不再是确定的了,而变成随机参数。这时的信号在某一时刻就要用三个随机变量来描述。如此可以推广到”个随机变量的情况。
函数与不等式和方程存在联系(初等函数)。令函数值等于零,从几何角度看,对应的自变量的值就是图像与X轴的交点的横坐标;从代数角度看,对应的自变量是方程的解。
另外,把函数的表达式(无表达式的函数除外)中的“=”换成“<”或“>”,再把“Y”换成其它代数式,函数就变成了不等式,可以求自变量的范围。
扩展资料:
将二维随机变量(X,Y)看成是平面上随机点的坐标,分布函数F(x,y)在(x,y)处的函数值就是随机点(X,Y)落在如图以(x,y)为顶点而位于该点左下方的无穷矩形区域内的概率。
相同的边缘分布可构成不同的联合分布,这反映出两个分量的结合方式不同,相依程度不同。这种差异在各自的边缘分布中没有表现,因而必须考察其联合分布。
参考资料来源:百度百科——联合分布函数
参考资料来源:百度百科——边缘分布函数
联合概率分布怎么做?
参考技术AX ,Y是独立的,算出X=x的概率,Y=y的概率,直接相乘。

联合概率分布简称联合分布,是两个及以上随机变量组成的随机变量的概率分布。根据随机变量的不同,联合概率分布的表示形式也不同。对于离散型随机变量,联合概率分布可以以列表的形式表示,也可以以函数的形式表示;对于连续型随机变量,联合概率分布通过非负函数的积分表示。
随机变量:给定样本空间 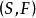 ,其上的实值函数
,其上的实值函数 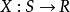 称为(实值)随机变量。如果随机变量X的取值是有限的或者是可数无穷尽的值,则称X为离散随机变量。如果X是由全部实数或者由一部分区间组成,则称X为连续随机变量,连续随机变量的值是不可数及无穷尽的。随机变量分为离散型随机变量和连续型随机变量,当要求随机变量的概率分布的时候,要分别处理。
称为(实值)随机变量。如果随机变量X的取值是有限的或者是可数无穷尽的值,则称X为离散随机变量。如果X是由全部实数或者由一部分区间组成,则称X为连续随机变量,连续随机变量的值是不可数及无穷尽的。随机变量分为离散型随机变量和连续型随机变量,当要求随机变量的概率分布的时候,要分别处理。
1. 离散型联合概率分布:
对于二维离散随机向量,设X和Y都是离散型随机变量, 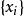 和
和 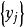 分别是X和Y的一切可能的几何,则X和Y的联合概率分布可以表示为如右图的列联表,也可以表示为如下的函数形式
分别是X和Y的一切可能的几何,则X和Y的联合概率分布可以表示为如右图的列联表,也可以表示为如下的函数形式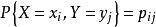 其中
其中
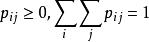
多维随机变量的中,只包含部分变量的概率分布称为边缘分布:
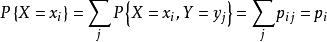
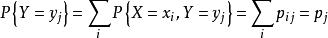
2. 连续型联合概率分布:
对于二维连续随机向量,设X和Y为连续型随机变量,其联合概率分布,或连续型随机变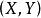 的概率分布
的概率分布 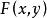 通过一非负函数
通过一非负函数 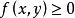 的积分表示,称函数
的积分表示,称函数 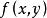 为联合概率密度。两者的关系如下:
为联合概率密度。两者的关系如下:
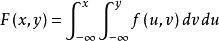
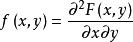
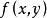 不但完全决定X和Y的联合概率分布,而且完全决定X的概率分布和Y的概率分布,以
不但完全决定X和Y的联合概率分布,而且完全决定X的概率分布和Y的概率分布,以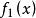 和
和 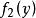 分别表示X和Y的概率密度,则
分别表示X和Y的概率密度,则
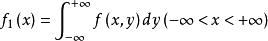
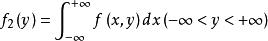
以上是关于如何求联合分布函数和边缘分布函数?的主要内容,如果未能解决你的问题,请参考以下文章