R语言-运筹学指派和运输问题实例
Posted 书槑
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了R语言-运筹学指派和运输问题实例相关的知识,希望对你有一定的参考价值。
这是我自己的运筹学笔记,由于老师讲的实在一言难尽,导致自己不得不对着英文教材自学,以下的例子就出自英文教材。
目录
问题提出
一家公司打算用三个基站生产四种产品,各基站的生产的成本如表9.27所示。除第2个基站不能生产第3种产品外,其他基站的生产都没有限制。表的最后一行是每种产品要求的生产量,最后一列是基站生产能力的限制。现在问题是如何进行生产分配。

我们有两种方法:
1.允许一种产品在两个基站分开生产;
2.不允许分开生产
接下来将对这两种方法依次进行分析。
第一种方法:运输问题
第一种方法实质是运输问题,基站即为产地,产品即为目的地,生产能力是供给,要求的生产量是需求。与运输问题一样,把基站2到产品3的运费设为M。由于总供给(75+75+45=195)超过总需求(20+30+30+40=120),因此设置一个75的虚拟需求来使得供需平衡,如表9.28所示。
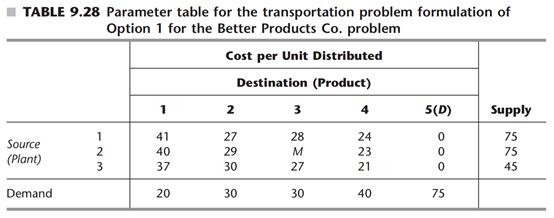
用R进行求解
library(lpSolve)
M = 100000000
a1 = c(41,27,28,24,0)
a2 = c(40,29,M,23,0)
a3 = c(37,30,27,21,0)
a = rbind(a1,a2,a3)
col.rhs = c(20,30,30,40,75) #最后一行
col.dir = rep('=',5)
row.rhs = c(75,75,45) #最后一列
row.dir = rep("=",3)
solution = lp.transport(a, row.signs = row.dir, row.rhs = row.rhs, col.signs = col.dir, col.rhs = col.rhs)
solution$solution
解得
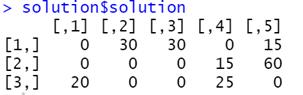
该矩阵表示各基站生产各产品的件数。
第二种方法:指派问题
一种产品只能在一个基站生产,实质是指派问题。每一个基站应当被分配至少一种产品,而由于基站3的生产能力只够生产一种产品,因此基站1或2要承担生产2种产品的责任。在此将基站1和2各拆分为2个子基站,a和b。则现在有5个基站,而只有4个产品,为保证每个基站都要生产一种产品,在此设置一个虚拟产品,即产品5,产品5会被分配给基站1或2。虚拟产品生产成本为0,且为了保证它不会被分配给基站3,将基站3生产的成本设为M。如表9.29所示,表内的数字表示每个基站生产对应产品的总成本,而非单价,例如第一个数字820即为表9.28中的41*20。注意只有指派问题用的是总成本,而之前的运输问题只需要用单价。
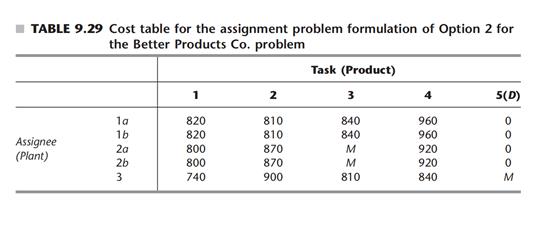
用R进行求解
library(lpSolve)
M = 100000000
a1 = c(820,810,840,960,0)
a2 = c(820,810,840,960,0)
a3 = c(800,870,M,920,0)
a4 = c(800,870,M,920,0)
a5 = c(740,900,810,840,M)
a = rbind(a1,a2,a3,a4,a5)
solution = lp.assign(a)
solution$solution
解得

去掉最后一列的虚拟产品,结果即为:基站1生产产品2和3,基站2生产产品1,基站3生产产品4。
参考教材:Introduction to Operations Research,Frederick S. Hillier • Gerald J. Lieberman
以上是关于R语言-运筹学指派和运输问题实例的主要内容,如果未能解决你的问题,请参考以下文章