数据结构与算法:树 二叉排序树(BST)

Posted 2022-12-06 史大拿

Tips: 采用java语言,关注博主,底部附有完整代码

工具:IDEA

本系列介绍的是数据结构: 树

这是第8篇目前计划一共有11篇:

1. 二叉树入门
2. 顺序二叉树
3. 线索化二叉树
4. 堆排序
5. 赫夫曼树(一)
6. 赫夫曼树(二)
7. 赫夫曼树(三)
8. 二叉排序树(BST)本篇
9. 平衡二叉排序树AVL
10. 2-3树,2-3-4树,B树 B+树 B*树 了解
11. 数据结构与算法:树 红黑树 (十一)

敬请期待吧~~

基本介绍

二叉排序树(Binary sort tree) 又叫做 二叉搜索树(binary search tree) ,是树形结构中的一种

定义:

• 非叶子结点外 他的每个左子结点都比当前结点小
• 非叶子结点外 他的每个右子结点都比当前结点大
• 如果一颗树只有树根,那么这也是 BST树

二叉排序树

先来看一张BST树:

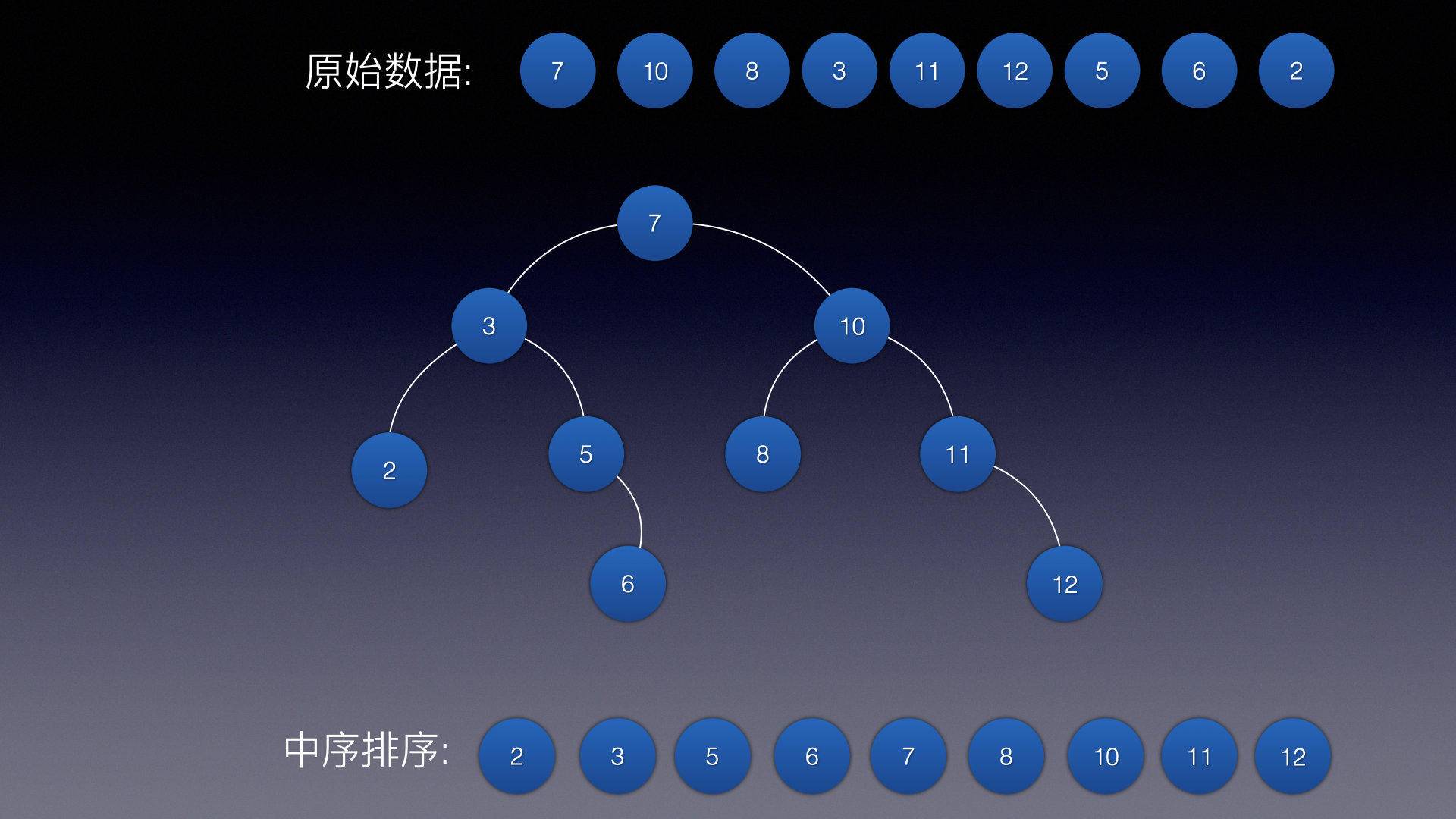
这是比较理想的情况,可以看出这棵树符合BST的定义

结点定义

public class SortTreeNode 

    int value;

    // 左子结点
    SortTreeNode leftNode;

    // 右子结点
    SortTreeNode rightNode;

    public SortTreeNode(int value) 
        this.value = value;
    

    @Override
    public String toString() 
        return "SortTreeNode" +
                "value=" + value +
                '';
    
  
     // region TODO 中序遍历
    public void show() 
        if (leftNode != null) 
            leftNode.show();
        
        System.out.println(this);

        if (rightNode != null) 
            rightNode.show();
        
    
    // endregion

    // region TODO 层序遍历
    public void showFloor() 
        Queue<SortTreeNode> queue = new LinkedList<>();
        queue.add(this);
        int index = 0;
        while (!queue.isEmpty()) 
            SortTreeNode removeNode = queue.remove();

            System.out.println("index" + (index++) + "层序遍历:" + removeNode);
            if (removeNode.leftNode != null) 
                queue.add(removeNode.leftNode);
            
            if (removeNode.rightNode != null) 
                queue.add(removeNode.rightNode);
            
        
    
    // endregion

这里非常简单,就是一个很普通的结点类

添加结点

思路:

• 如果要添加的结点比当前结点大,添加到右子结点上
  • 右子结点 == null , 直接添加到右子结点
  • 右子结点 != null, 进行下一轮递归
• 如果要添加的结点比当前结点小,添加到左子结点上
  • 左子结点 == null, 直接添加到左子结点上
  • 左子结点 != null,进行下一轮递归

添加的代码非常简单:

# SortTreeNode.java
// 添加结点  
public void add(SortTreeNode node) 
    if (node == null) 
        return;
    

    // 如果传入的结点 <= 当前结点
    // 说明当前结点应该存放在左子结点上
    if (node.value <= value) 
        // 如果左子结点为null 说明是叶子结点 直接存放即可
        if (leftNode == null) 
            leftNode = node;
         else 
            leftNode.add(node);
        
    
    // 如果传入的结点 >= 当前结点
    // 说明当前结点应该存放在右子结点上
    if (node.value >= value) 
        // 如果左子结点为null 说明是叶子结点 直接存放即可
        if (rightNode == null) 
            rightNode = node;
         else 
            rightNode.add(node);
        
    

添加完整流程图:

如果二叉排序树成功的话,配合中序遍历,正好是有序的!

搜索结点

搜索结点分为2种情况:

• 搜索当前结点
• 搜索当前结点的父结点

搜索当前结点好理解, 为什么要搜索当前结点的父结点呢?

这里是为了删除结点做准备

因为删除结点得通过 parent.leftNode = null || parent.rightNode = null 来进行删除

这样删除的是指针对象

而不是通过 currentNode.leftNode = null || currentNode .rightNode 来进行删除

这样删除只是吧一个变量删除了,并没有任何意义!!

搜索当前结点

思路和添加结点思路有异曲同工之妙:

• 如果当前结点 > 需要查找的结点,那么就去右子结点上找
• 如果当前结点 < 需要查找的结点,那么就去左子结点上找

理想状态下和二分查找很想!

# SortTreeNode.java

// @param return: 没有找到返回null
public SortTreeNode search(int value) 
//        System.out.println("search" + this.value + "\\tvalue" + value);

        // 需要找的结点 = 如果当前结点
        if (value == this.value) 
            return this;
         else if (value < this.value) 
            // 继续找左子结点
            if (leftNode != null) 
                return leftNode.search(value);
            
         else 
            // 继续找右子结点
            if (rightNode != null) 
                return rightNode.search(value);
            
        
        return null;
    

搜索父结点

搜索父结点有所不同,以上面提到的 BST树来举例:

可以看出, 8结点 和 11 结点的父结点都是10

来看看完整代码:

# SortTreeNode.java
  
public SortTreeNode searchParent(int value) 
    // 左子结点 != null 并且左子结点 == 当前结点
    boolean isLeftCompare = (leftNode != null && leftNode.value == value);
    boolean isRightCompare = (rightNode != null && rightNode.value == value);

    // 如果左子结点 或者右子结点相同 说明找到了父结点
    if (isLeftCompare || isRightCompare) 
        return this;
     else if (value < this.value && leftNode != null) 
        // 当前结点 < 需要查找的结点  并且 左子结点不为null 继续向左找
        return leftNode.searchParent(value);
     else 
        if (rightNode != null) 
            return rightNode.searchParent(value);
        
    
    return null;

这段代码细品一下还是不难的.

删除结点

删除结点分为3种情况:

• 删除叶子结点
• 删除只有1个结点的结点
• 删除有2个结点的结点

删除叶子结点	直接删除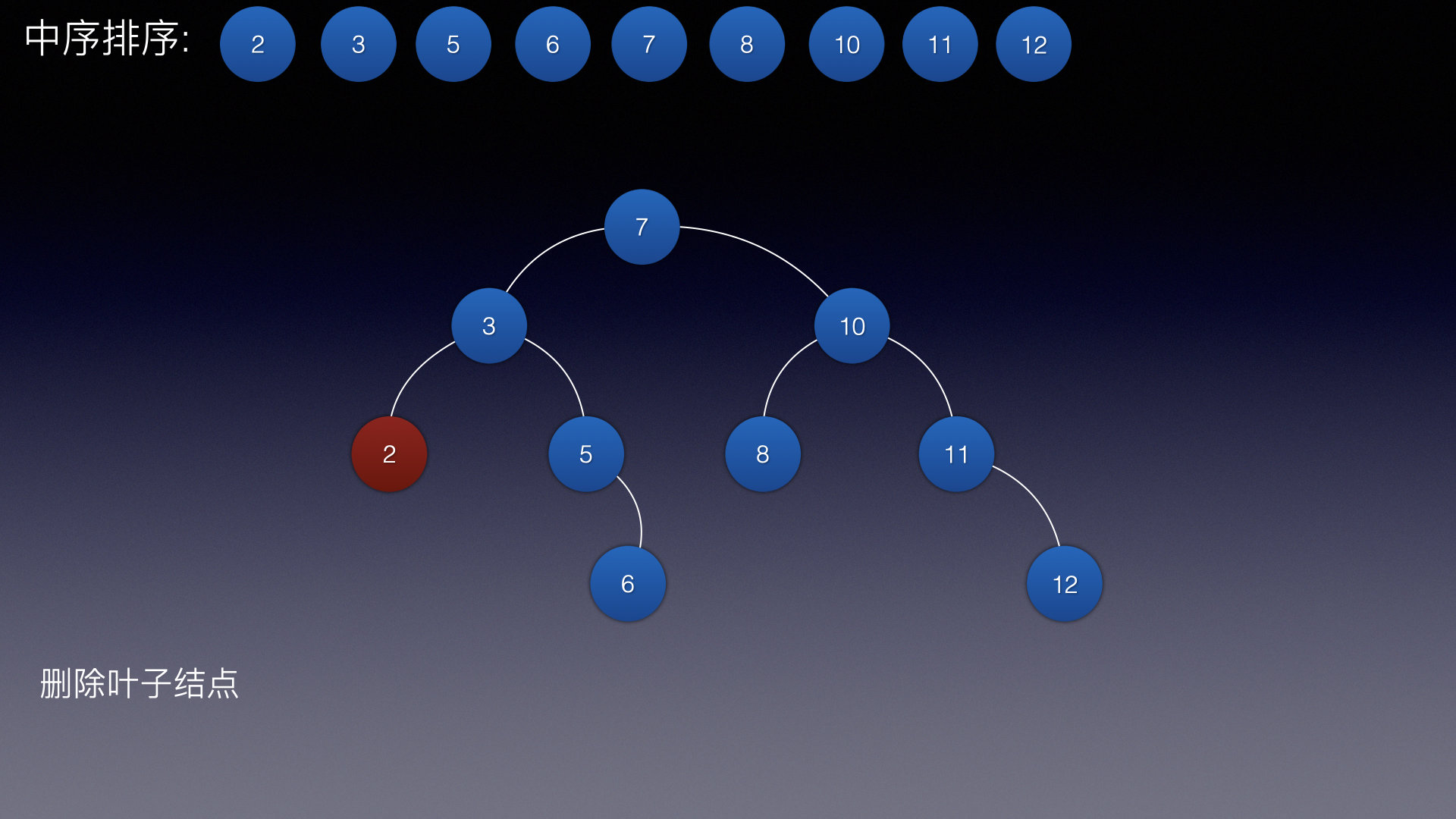
删除只有1个结点的结点	让删除结点的子结点代替删除结点位置
删除有2个结点的结点	找到删除结点的后继结点代替删除即结点位置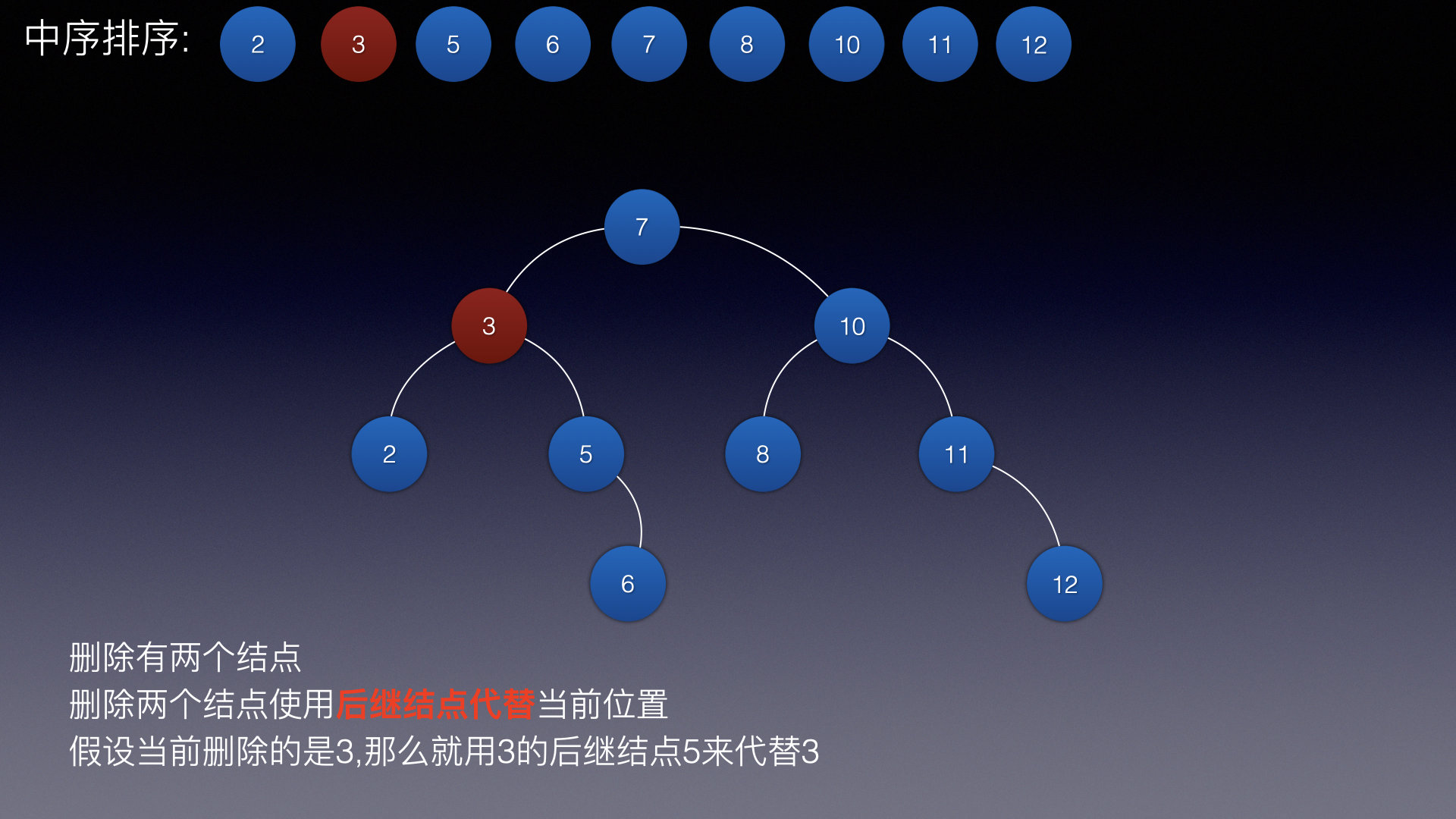

删除叶子结点

// 删除结点
public void del(int value) 
    // TODO 当前结点
    SortTreeNode searchNode = search(value);

    if (searchNode == null) 
        System.out.println("没有找到结点");
        return;
    

    // TODO 当前结点的父结点
    SortTreeNode searchParentNode = searchParent(value);
  
    // TODO 删除叶子结点
  	if (searchNode.leftNode == null && searchNode.rightNode == null) 
      // 如果左子结点和当前结点相同 那么就删除左子结点
      if (searchParentNode.leftNode == searchNode) 
          searchParentNode.leftNode = null;
      
      // 反之删除右子结点
      if (searchParentNode.rightNode == searchNode) 
          searchParentNode.rightNode = null;
      
    
	

不好理解可以看着图来理解:

当前结点 是 2

父结点 是 3

删除只有一个子结点

public void del(int value) 

    // TODO 当前结点
    SortTreeNode searchNode = search(value);

    if (searchNode == null) 
        System.out.println("没有找到结点");
        return;
    

    // TODO 当前结点的父结点
    SortTreeNode searchParentNode = searchParent(value);
  
    // TODO 删除叶子结点
    if (searchNode.leftNode == null && searchNode.rightNode == null) 
      	....
     else if (searchNode.leftNode == null) 
        // TODO 删除只有一个叶子结点
        // 如果左子结点为null 说明右子结点不为null

        // 如果当前是左子结点
        if (searchParentNode.leftNode == searchNode) 
          // 那么就让左子结点 = 当前元素的右子结点 达到删除的目的
          searchParentNode.leftNode = searchNode.rightNode;
        
        if (searchParentNode.rightNode == searchNode) 
          searchParentNode.rightNode = searchNode.rightNode;
        
     else if (searchNode.rightNode == null) 
        // TODO 删除只有一个叶子结点
        // 和上边同理
        if (searchParentNode.leftNode == searchNode) 
          searchParentNode.leftNode = searchNode.leftNode;
        
        if (searchParentNode.rightNode == searchNode) 
          searchParentNode.rightNode = searchNode.leftNode;
        
      

还是同理,逻辑不清晰的看图说话

当前结点是5

父结点是3

删除有2个结点的结点

如果删除2个结点的结点,那么他是通过后继结点来代替当前结点位置

思路:

• 寻找后继结点, 按照中序遍历的思路,后继结点在当前结点的右子结点的最左侧
• 找到后继结点后吧后继结点删除掉,然后让当前结点的值 = 后继结点即可

tips: 这里其实说白了没有进行删除,只是进行了值的替换,达到了“删除”的效果,具体删除的只是后继结点

假设当前删除的元素是3,那么就找到他的后继结点

上边也说过,后继结点是当前结点的右子结点的最左边

这里当前结点只有右子结点,所以后继结点就是5

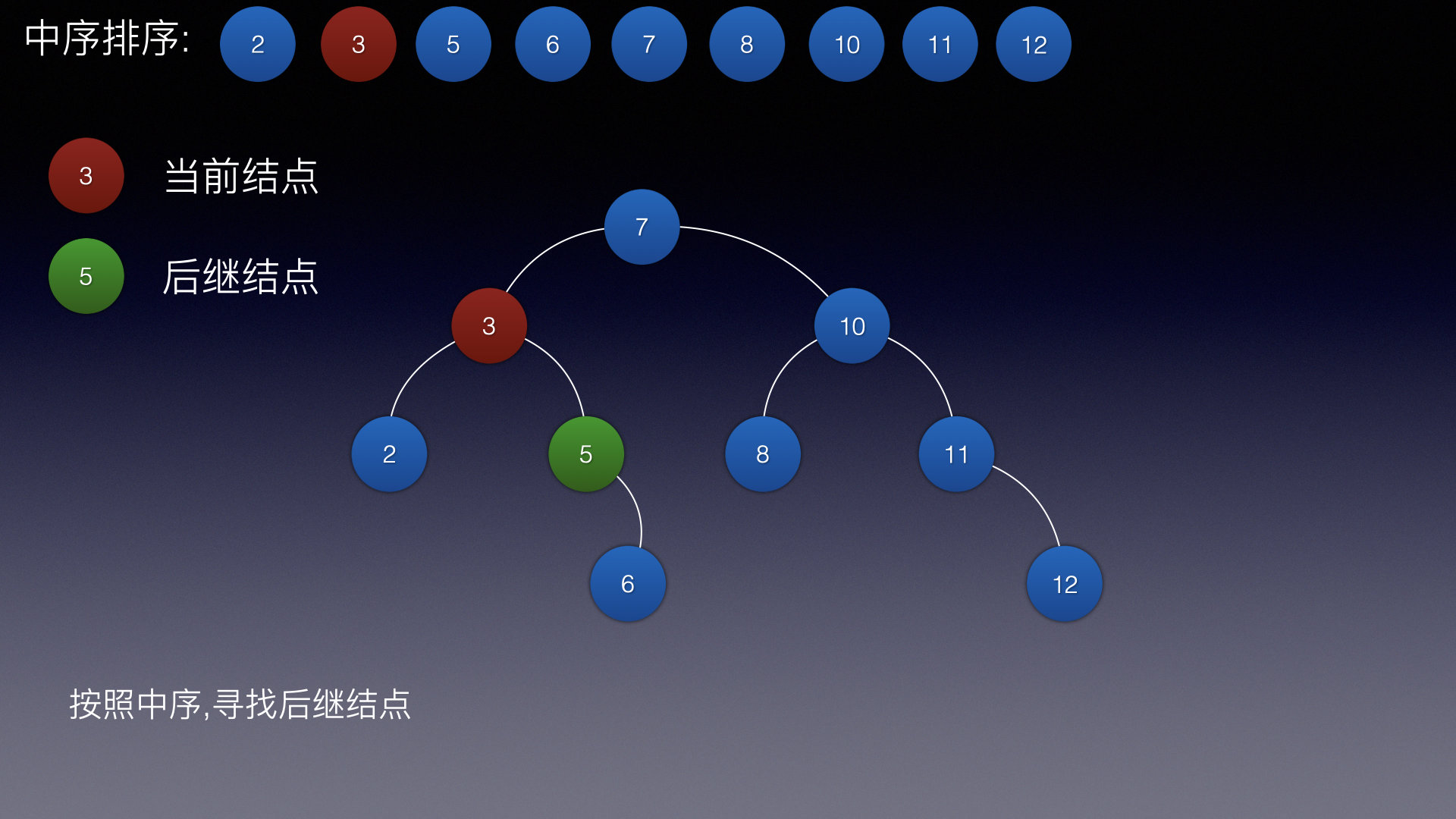
然后在吧5删除掉,就变成了删除一个结点的结点,就变成了这样

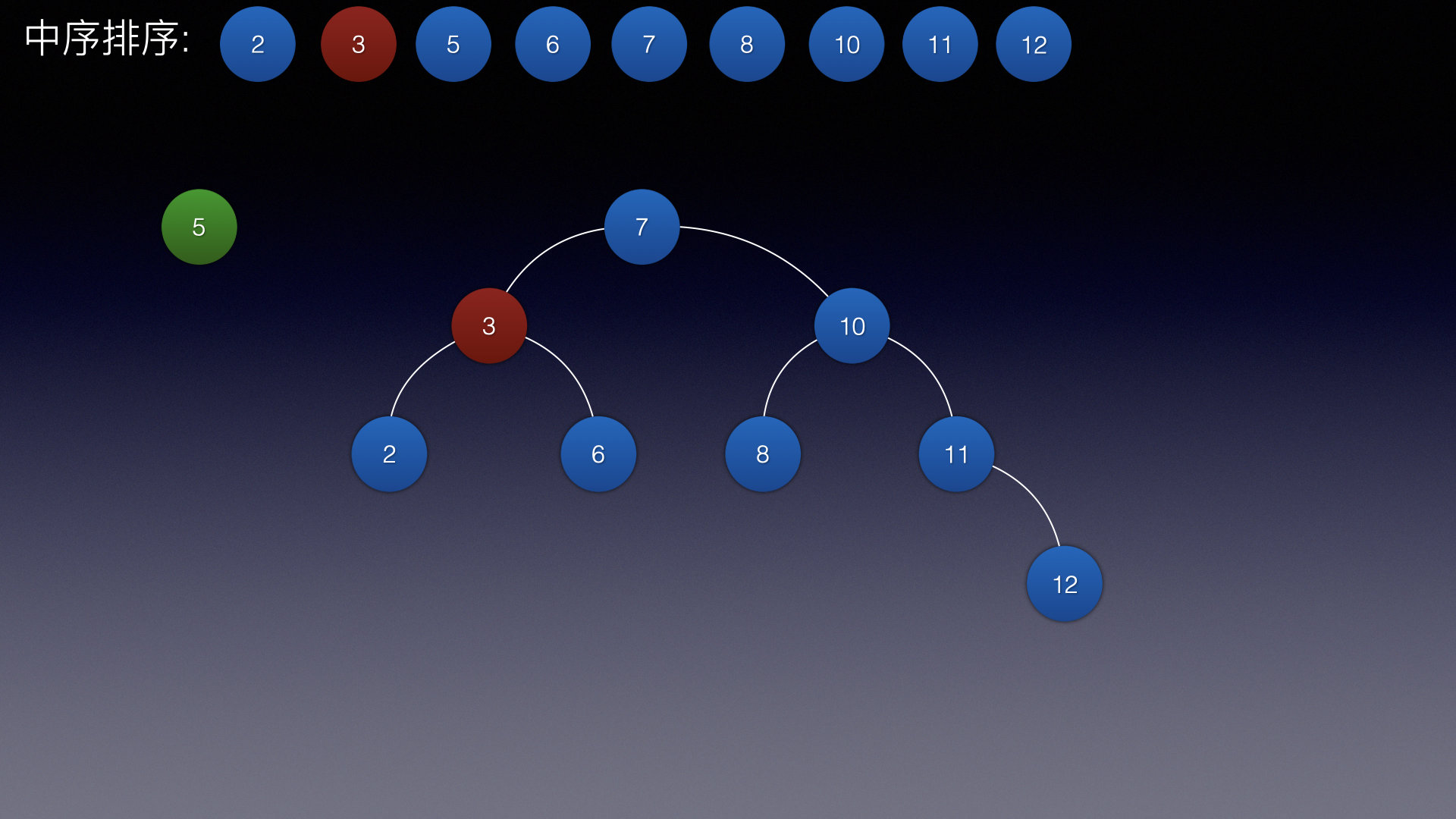
最后将后继结点的值替换到当前结点上,就达到了删除的效果

思路也很简单,那就来看看完整代码:

public void del(int value) 

  // TODO 当前结点
  SortTreeNode searchNode = search(value);

    if (searchNode == null) 
      System.out.println("没有找到结点");
      return;
    

    // TODO 当前结点的父结点
    SortTreeNode searchParentNode = searchParent(value);

    // 左子结点和右子结点为null 说明是叶子结点
    // TODO 删除叶子结点
    if (searchNode.leftNode == null && searchNode.rightNode == null) 
      ....
     else if (searchNode.leftNode == null) 
      // TODO 删除只有一个叶子结点
      .....
     else if (searchNode.rightNode == null) 
      // TODO 删除只有一个叶子结点
      // 和上边同理
      .....
     else 
      // TODO 左子结点和右子结点都有值!

      // 此时结点为要删除结点的 后继结点
      // 后继结点在右子结点的最左侧
      SortTreeNode lastNode = delDoubleTree(searchNode.rightNode);

      // 当前结点 = 后继结点即可
      searchNode.value = lastNode.value;
    


// 删除有两个结点的树
public SortTreeNode delDoubleTree(SortTreeNode node) 
    SortTreeNode temp = node;

    // 寻找到后继结点
    while (temp.leftNode != null) 
        temp = temp.leftNode;
    

    // 删除当前最小值
    del(temp.value);
    // 返回当前结点
    return temp;

执行到这里,删除结点就完事了!

理想状态和不理想状态

理想状态

上边提到的这颗树就是比较理想状态,因为左子结点和右子结点基本一样高

这样的话删除,搜索,的速度还是很可观的

不理想状态

有理想状态肯定有不理想状态, 那么非常极端的不理想状态就是这样:

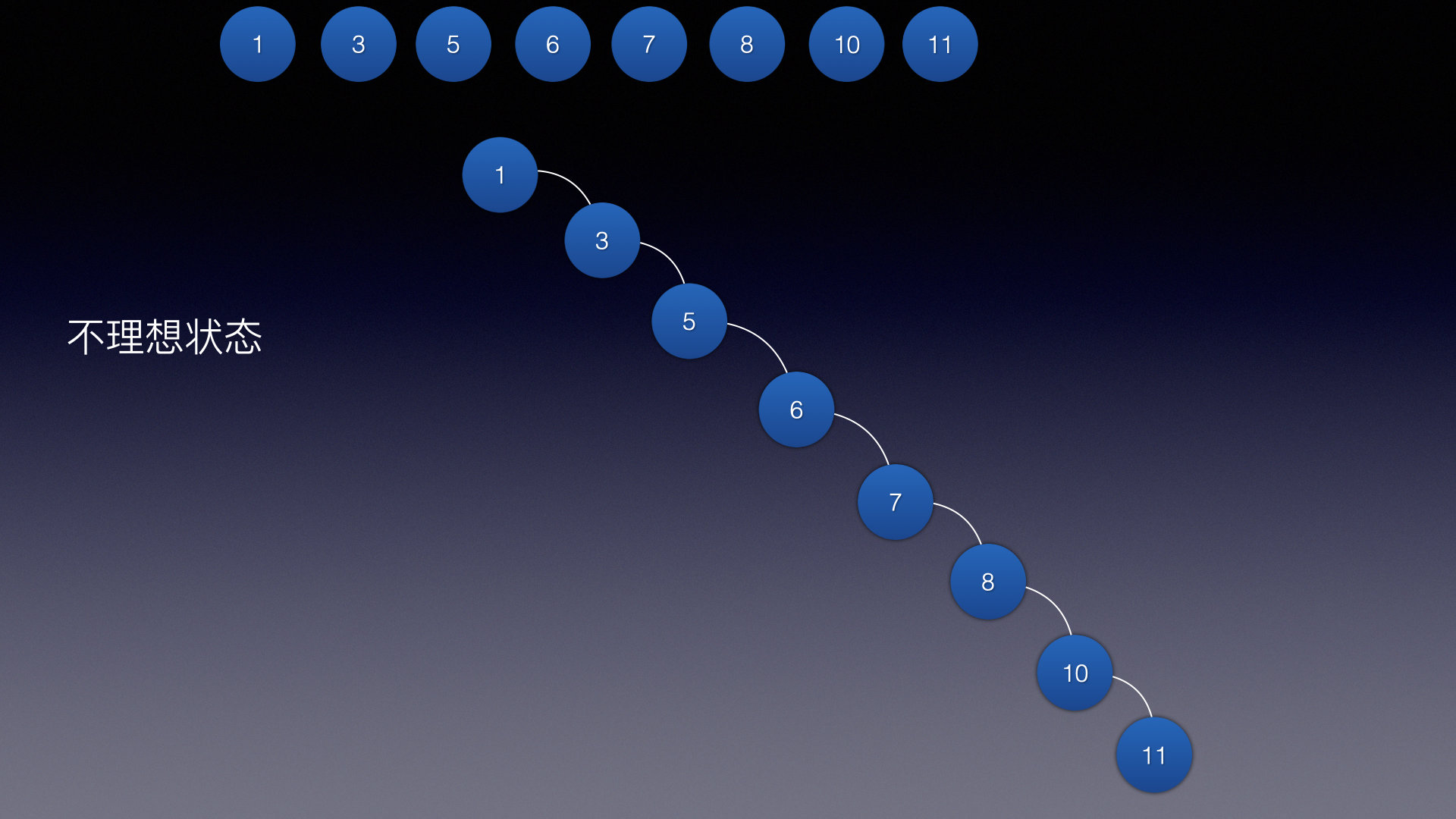
可以看出,这样的话感觉像是链表一样,如果要搜索,删除结点也很不友好…

优点:

• 比较基础的树结构,能够通过中序遍历进行排序

• 代码比较简单

• 理想状态下效果还可以

缺点:

• 如果不理想状态,效果极差

这里就引出了下一篇 (AVL 平衡二叉树)!,AVL树就是为了解决这种很奇怪的现象

调用:

public static void main(String[] args) 

        int[] tempInts = 10, 8, 3, 11, 12, 5, 6, 2;

        // 规则: 左子结点 >= 当前结点 > 右子结点

        SortTreeNode root = new SortTreeNode(7);
        for (int tempInt : tempInts) 
            root.add(new SortTreeNode(tempInt));
        

        System.out.println("length" + tempInts.length);

//        test(root);

        // 层序: 7 3 10 2 5 8 11 6 12
        // 中序: 2 3 5 6 7 8 10 11 12
        System.out.println("原始数据");
        root.show();

        root.del(7);
        System.out.println("删除后®");
        root.show();
    

这里就偷个懒没有写tree类,直接操作的是rootNode… 大家别学我,还是规范一点比较好 @__@

完整代码

原创不易,您的点赞就是对我最大的支持!

其他树结构文章:

1. 二叉树入门
2. 顺序二叉树
3. 线索化二叉树
4. 堆排序
5. 赫夫曼树(一)
6. 赫夫曼树(二)
7. 赫夫曼树(三)
8. 二叉排序树(BST)本篇
9. 平衡二叉排序树AVL
10. 2-3树,2-3-4树,B树 B+树 B*树 了解
11. 数据结构与算法:树 红黑树 (十一)