Python大作业耦合网络信息传播
Posted Dreamchaser追梦
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python大作业耦合网络信息传播相关的知识,希望对你有一定的参考价值。
文章目录
前言
说实话,已经好久没写博文了,上篇博文的时间都是两个月前。但在这种情况下,粉丝蹭蹭往上涨,hh,这属实是我没想到的,让我着实有种愧疚感。
当然最近没写博文,除了找不到合适的题材外,最重要的是最近有亿点点忙(上课、实验报告、健身、做项目、开会…)剩下的时间都是零零散散,没办法静下心来写东西。
这次主要是趁着要写实验报告,所以顺手将实验报告的思路改写成博文,而作业题目也挺有意思的,是耦合网络信息传播,可以模拟病毒扩散或者信息的扩散,听着是不是有种高大上的感觉?所以我把它写作博文供大家学习参考。(又水了一篇~)
注:本博文代码仅供学习交流,谢绝抄袭!
一、题目介绍
作业题目是一个PPT文件,上来就是一个大标题

第二页就是解题思路(说实话有些突兀,我连题目都不知道是啥就开始叫我一步步做下去,属实有点懵了,这里最好加一个具体的问题,比如用Python编写程序模拟耦合网络的信息传播)




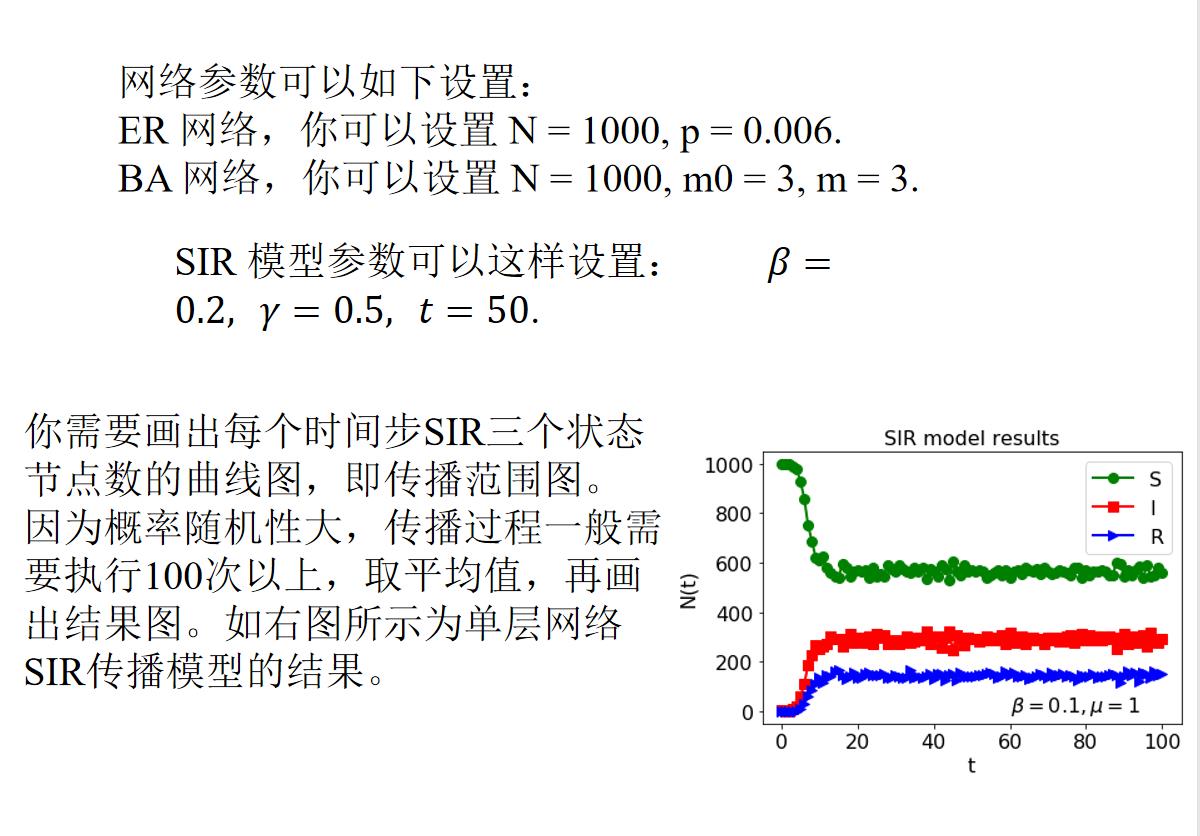
以上便是题目的PPT内容。
二、解题思路
题目内容大致是要我们编写程序模拟耦合网络的信息传播。
解题思路PPT文件其实已经告诉我们了,我们只需按照PPT的步骤一步步进行代码复现即可。
1.构造一个耦合网络
按照PPT的意思,应该是要我们构造一个ER-BA双层网络。
①构造ER网络
生成ER随机网络(算法):
初始: 网络总结点数 N, 没有边;
网络构建过程:每对节点以概率 p 被选择,进行连边,不允许重复连边。
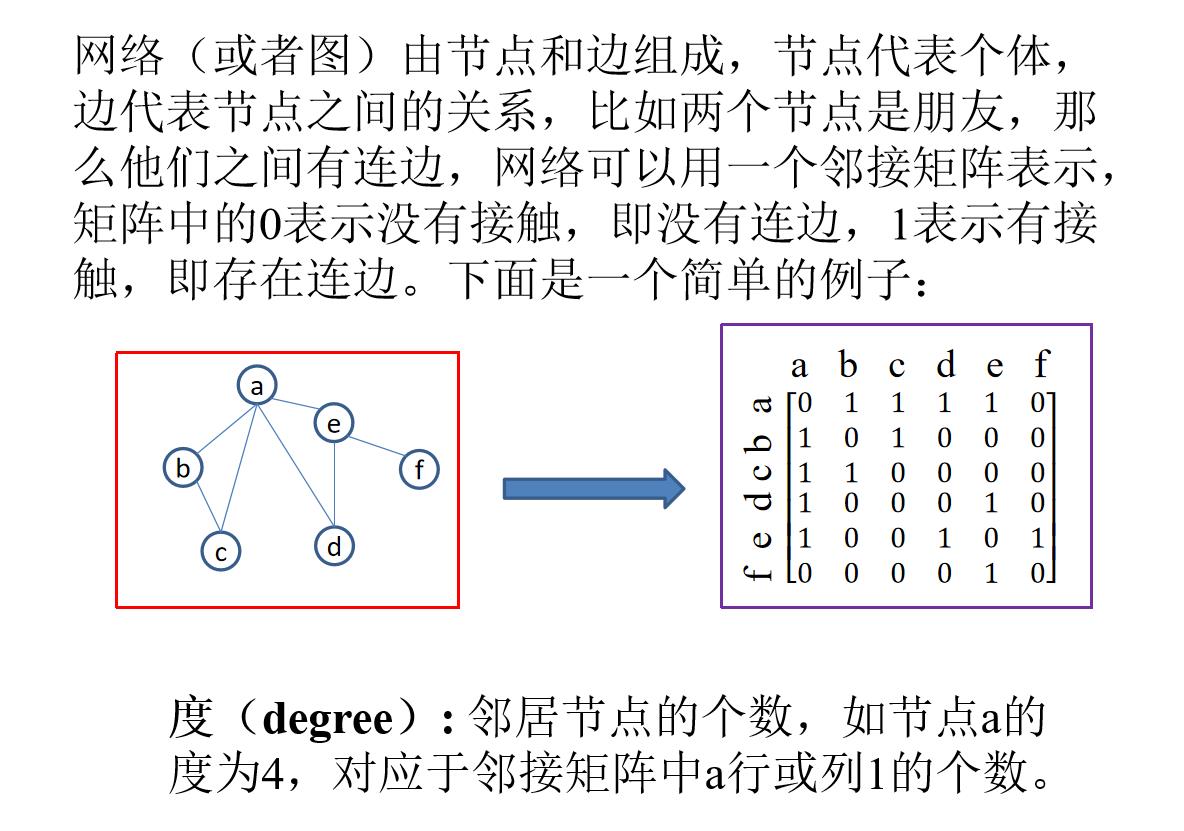
我这里用邻接矩阵(对于Python就是一个二维列表)来存储网络,ER[i][j]==1就说明i和j节点之间有连线,反之无连线。这里用一个全局二维数组变量ER来存储。
根据生成的规则我们编写如下代码来生成ER随机网络(注意这里方法的封装,把这些可变的概率、节点数当做入参,以便后续改变参数),这里我们利用random.random()方法来模拟概率,当随机生成的数字小于概率就生成该边。
# ER随机网络
ER = [[]]
# 生成ER随机网络,n表示点个数,p表示生成边的概率
def generateER(n, p):
global ER
# 这种方式声明可以避免浅拷贝问题
ER = [([0] * n) for i in range(n)]
for i in range(0, n):
for j in range(i + 1, n):
# 随机生成的数
x = random.random()
# 概率生成边
if x < p:
ER[i][j] = 1
ER[j][i] = 1
②构造BA网络
BA无标度网络
(1) 初始时网络有 m_0 个节点,可以没有边,也可以像ER网络一样生成一些边;也可以前m_0 个节点是全连通结构。 (2)
每个时间步,一个新节点加入这个网络,并从已存在的网络中选择 m个节点(m≤m_0) 与之相连,选择概率 p_i 与已存在的节点 i的度成正比 p_i=k_i/∑_j▒k_j(3) 当网络中存在 N 个节点后,停止。
同样BA无标度网络也是以邻接矩阵来存储,这里按照给定的规则进行编码。
考虑到规则比较复杂,可以分为以下几个步骤:
- 初始化BA网络,此时BA网络只有m0个初始节点,边关系随意
- 迭代增加m个节点,每增加一个节点便去根据规则概率寻找m个节点
上述逻辑实现有些复杂,这里我们简化条件来实现题目要求的效果:
- 假设每次增加节点时至少有m个度不为0的节点(因为如果没有m个度不为0的节点,这就意味着我们需要考虑度为0的情况)
- 初始m0个节点组成的网络为全连通网络
由于每次增加节点时选取m个节点操作过于复杂,所以我将其封装为一个方法来增加代码可读性。
以下是代码实现:
# BA无标度网络
BA = [[]]
# 在下标0到end的klist列表中根据k的权重来寻找一个下标返回,不包括exclude_list中的节点
def findOne(klist, end, exclude_list):
flag = True
k_sum = 0
for i in range(0, end):
k_sum += klist[i]
result = end - 1
while flag:
x = random.random() * k_sum
pre = 0
for i in range(0, end):
pre += klist[i]
if pre > x:
result = i
break
flag = False
# 检查结果是否在exclude_list中,如果是则重来,否则返回结果
for i in exclude_list:
if i == result:
flag = True
break
return result
# 根据BA无标度网络的规则在klist(下标为0到end 之间)中寻找m个数
# 为了简化逻辑,这里参与竞争(k!=0)的节点数必定大于m
def find(k_list, m, end):
# 结果数组
result = []
# 初始化
for i in range(0, m):
j = findOne(k_list, end, result)
# 增加结果
result.append(j)
return result
# 生成BA无标度网络,n表示点个数,m0表示初始节点数
def generateBA(n, m0, m):
global BA
# 初始BA无标度网络(利用生成器创建避免浅拷贝)
BA = [([0] * n) for i in range(n)]
# 初始化前m0个节点都为连通网络
for i in range(0, m0):
for j in range(i + 1, m0):
BA[i][j] = 1
BA[j][i] = 1
# 初始度数组
k_list = [m0 - 1] * m0 + [0] * (n - m)
# 遍历后面的节点,模拟加入
for i in range(m0, n):
# 选出m个节点
nodes = find(k_list, m, i)
for j in nodes:
BA[i][j] = 1
BA[j][i] = 1
# 更新度数组
k_list[i] += 1
k_list[j] += 1
③双层ER-BA网络模型
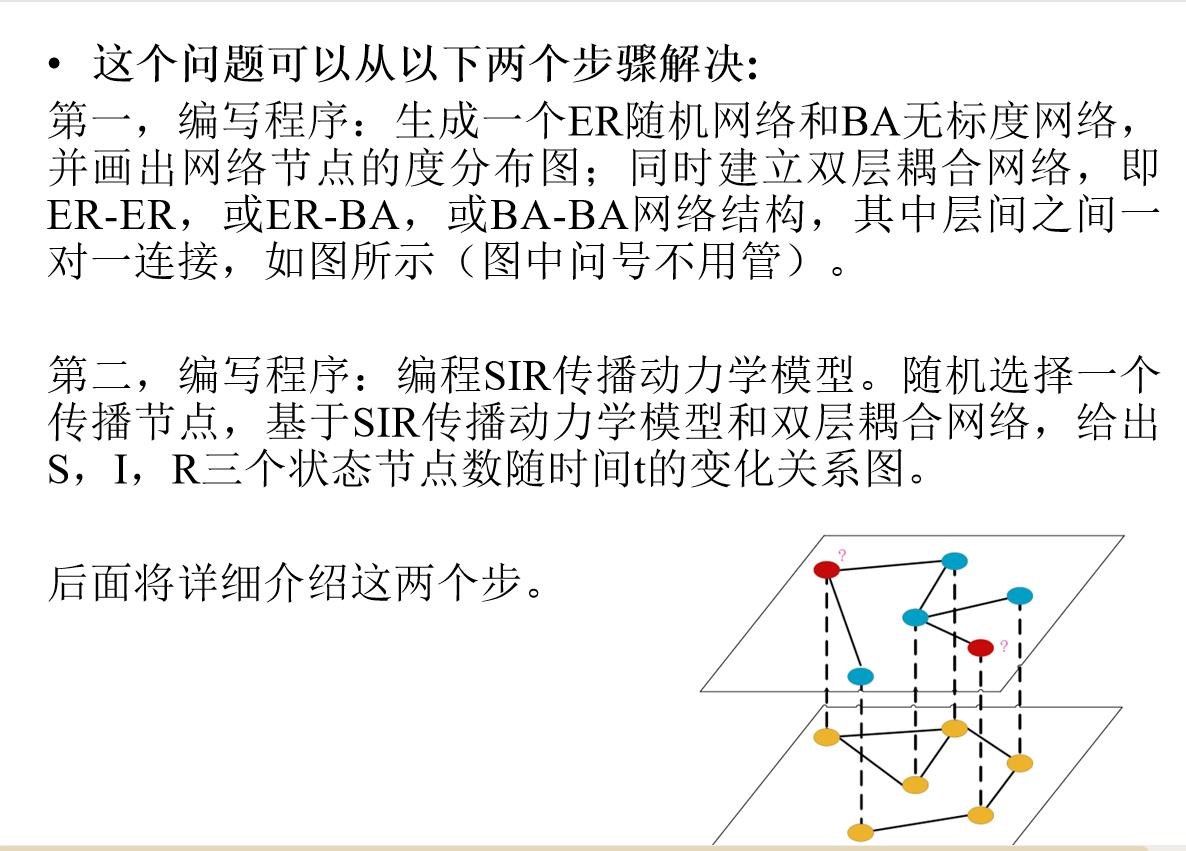
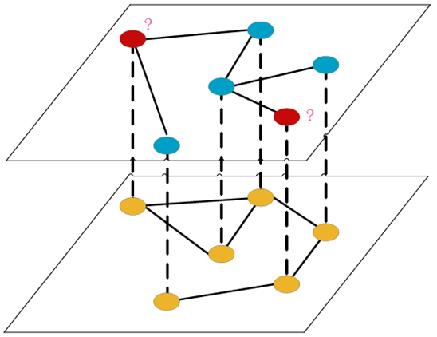
构建出双层网络结构(如ER-ER网卡,ER-BA网络,BA-BA网络),假设层间节点一对一连接,如下图所示。可以理解不同社交平台相互耦合。

这里不需要代码操作,但是我们需要理解,ER节点和BA节点是一一对应的,就像上图展示的那样。
在代码中可以理解为ER网络中下标为i的节点和BA网络中下标为i的节点实际上是连通的。
2.利用SIR模型来模拟信息传播
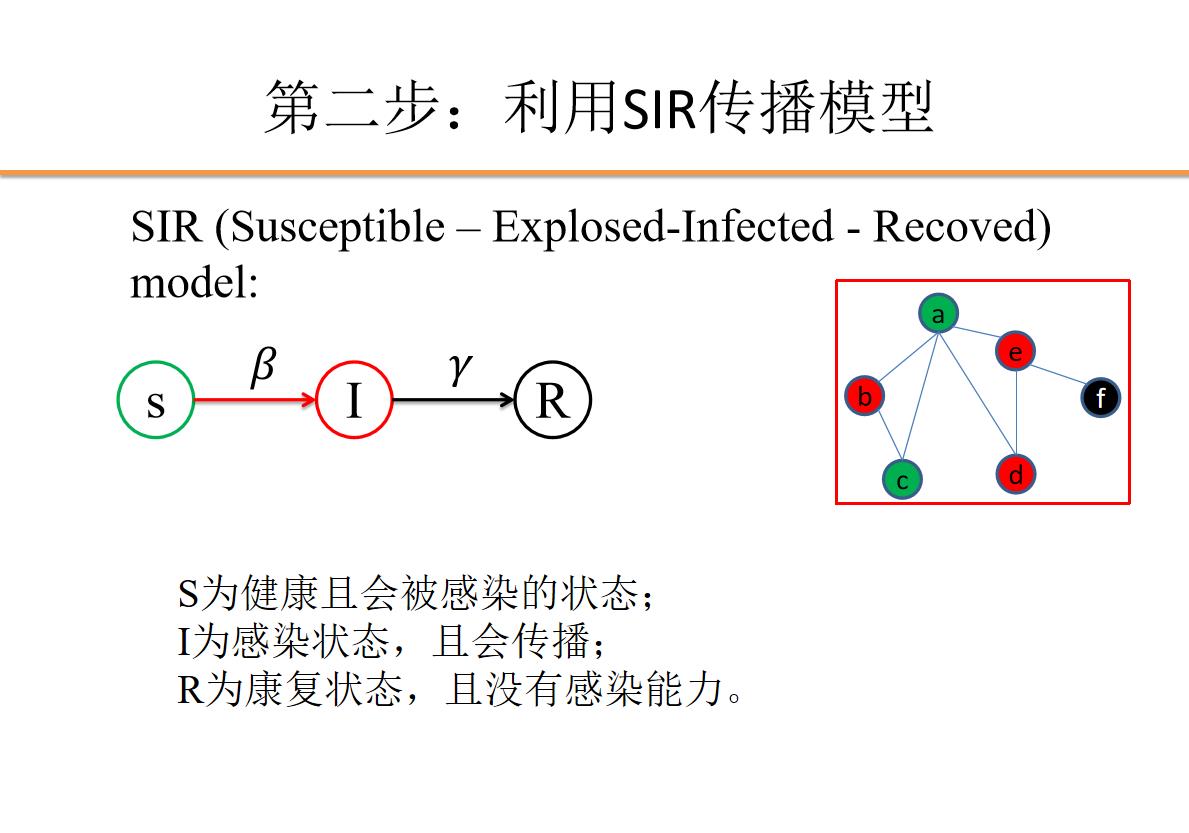
SIR (Susceptible – Infected - Recoved) model:
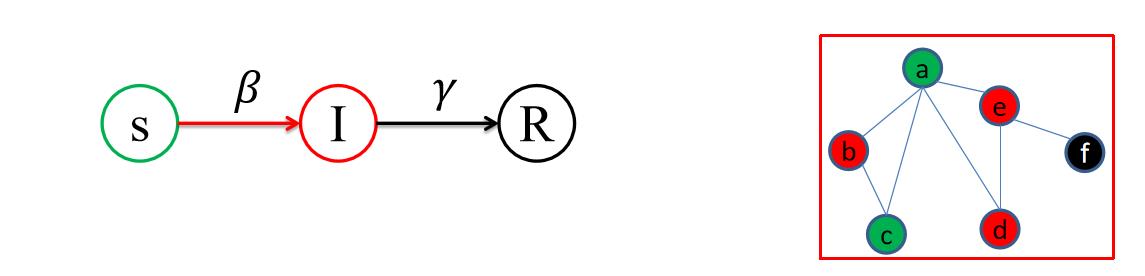
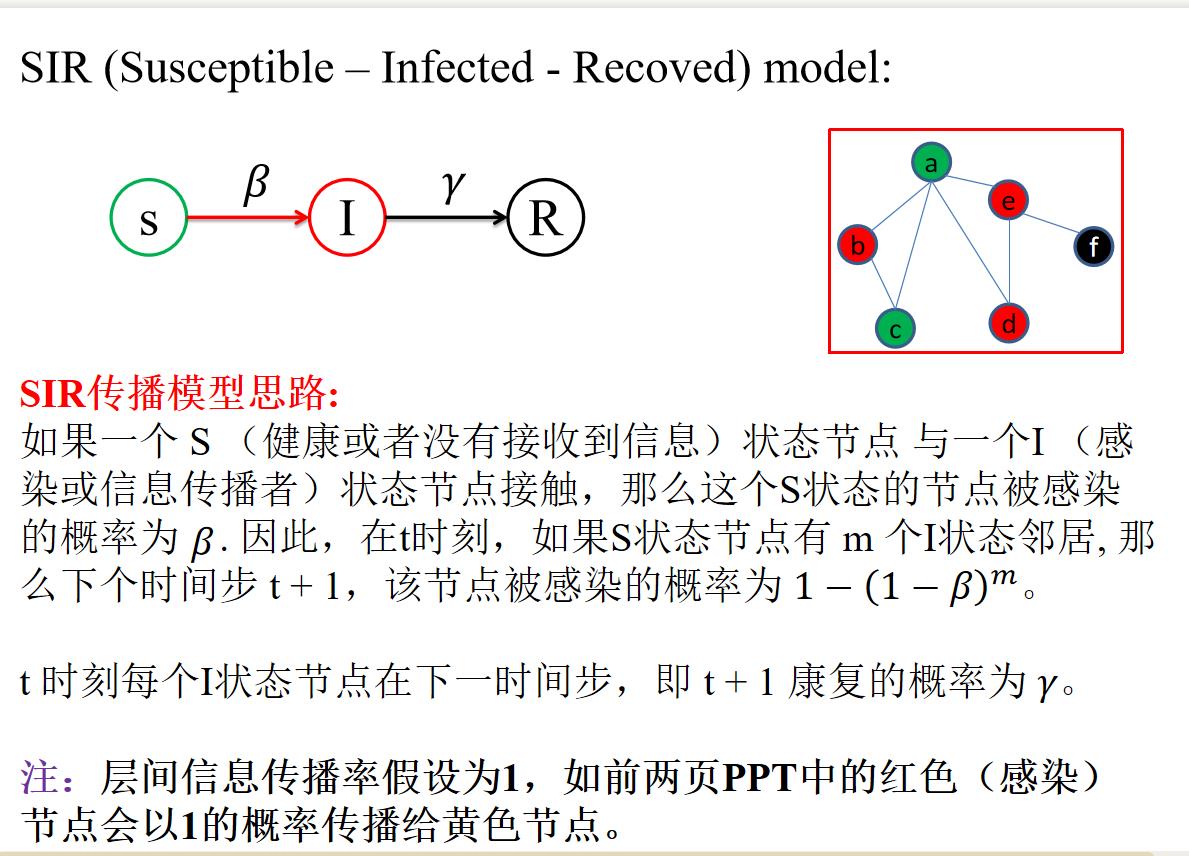
SIR传播模型思路:
如果一个 S (健康或者没有接收到信息)状态节点 与一个I (感染或信息传播者)状态节点接触,那么这个S状态的节点被感染的概率为 β .
因此,在t时刻,如果S状态节点有 m 个I状态邻居, 那么下个时间步 t + 1,该节点被感染的概率为 1−(1−β)^m。t 时刻每个I状态节点在下一时间步,即 t + 1 康复的概率为 γ。
我们可以将上述思路转化为以下步骤:
1.初始一个感染点
2.迭代循环t模拟时间步,每次迭代,每个节点都会根据规则刷新状态
- 如果节点状态为S(正常,未被感染),则它有1−(1−β)^m的概率被感染成I状态
- 如果节点状态为I(被感染),则它有γ的概率康复转变为R状态
- 如果节点状态为R,则状态不会改变(模拟病毒免疫)
3.记录每个时间点的S节点数、I节点数、R节点数
在这里需要注意的是,在考虑周围感染节点时,别忘了考虑ER-BA网络“上下层”的感染情况,因为这里ER网络和BA网络对应的节点时连通的。
这里写代码时也要考虑到入参,同时对于复杂的逻辑进行另外的封装以实现良好的代码可读性,以下是代码实现:
# ER网络感染的情况,S表示为健康,I表示已感染,R表示已康复
ER_SIR = []
BA_SIR = []
# 用于记录每日数据的数组
slist = []
ilist = []
rlist = []
# 对ER网络的i节点进行处理,i表示节点下标,t表示天数,b表示感染系数,y表示康复系数
def er_sir_one(i, t, b, y):
global ER, BA, ER_SIR, BA_SIR, slist, ilist, rlist
if ER_SIR[i] == 'S':
# 开始统计周围节点感染的数量
inum = 0
for x in range(len(ER_SIR)):
if (not x == i) and ER[i][x] == 1 and ER_SIR[x] == 'I':
inum += 1
# 因为是双层网络,所以BA也要考虑
if BA_SIR[i] == 'I':
inum += 1
ilist[t] += 1
p = random.random()
# 有1-(1-b)^inum概率感染
if p < 1 - (1 - b) ** inum:
ER_SIR[i] = 'I'
ilist[t] += 1
return
slist[t] += 1
elif ER_SIR[i] == 'I':
p = random.random()
# 有y的几率康复
if p < y:
ER_SIR[i] = 'R'
rlist[t] += 1
return
ilist[t] += 1
else:
rlist[t] += 1
# 对BA网络的i节点进行处理,i表示节点下标,t表示天数,b表示感染系数,y表示康复系数
def ba_sir_one(i, t, b, y):
global ER, BA, ER_SIR, BA_SIR, slist, ilist, rlist
if BA_SIR[i] == 'S':
# 开始统计周围节点感染的数量
inum = 0
for x in range(len(BA_SIR)):
if (not x == i) and BA[i][x] == 1 and BA_SIR[x] == 'I':
inum += 1
# 因为是双层网络,所以ER也要考虑
if ER_SIR[i] == 'I':
inum += 1
p = random.random()
# 有1-(1-b)^inum概率感染
if p < 1 - (1 - b) ** inum:
BA_SIR[i] = 'I'
ilist[t] += 1
return
slist[t] += 1
# 有y的几率康复
elif BA_SIR[i] == 'I':
p = random.random()
if p < y:
BA_SIR[i] = 'R'
rlist[t] += 1
return
ilist[t] += 1
else:
rlist[t]+=1
def sir(b, y, t):
global ER_SIR, BA_SIR, slist, ilist, rlist
n = len(ER[0])
# 初始化ER_SIR,BA_SIR
ER_SIR = ['S'] * n
BA_SIR = ['S'] * n
# 初始化每日统计数据的数组
slist = [0] * t
ilist = [0] * t
rlist = [0] * t
# 随机感染ER网络中的一个节点
x = random.randint(0, n - 1)
ER_SIR[x] = 'I'
# 遍历t天,模拟过了t天
for day in range(t):
# 遍历所有节点
for node in range(n):
# 对双层网络状态进行一遍刷新
er_sir_one(node, day, b, y)
ba_sir_one(node, day, b, y)
3.画图
最后便是根据要求将结果以图表方式可视化展现,这里用了matplotlib这个包,以下是代码实现:
# 画图
plt.plot(list(range(t)), slist, linewidth=4,label=u'S')
plt.plot(list(range(t)), ilist, linewidth=4,label=u'I')
plt.plot(list(range(t)), rlist, linewidth=4,label=u'R')
plt.legend() # 让图例生效
plt.xlabel(u"t") # X轴标签
plt.ylabel("N(t)") # Y轴标签
plt.title("SIR model result") # 标题
plt.show()
三、完整代码
以下是完整代码实现:
import random
import matplotlib.pyplot as plt
# ER随机网络
ER = [[]],
# BA无标度网络
BA = [[]]
# ER网络感染的情况,S表示为健康,I表示已感染,R表示已康复
ER_SIR = []
BA_SIR = []
# 用于记录每日数据的数组
slist = []
ilist = []
rlist = []
# 生成ER随机网络,n表示点个数,p表示生成边的概率
def generateER(n, p):
global ER
# 避免浅拷贝
ER = [([0] * n) for i in range(n)]
for i in range(0, n):
for j in range(i + 1, n):
# 随机生成的数
x = random.random()
# 概率生成边
if x < p:
ER[i][j] = 1
ER[j][i] = 1
# 在下标0到end的klist列表中根据k的权重来寻找一个下标返回,不包括exclude_list中的节点
def findOne(klist, end, exclude_list):
flag = True
k_sum = 0
for i in range(0, end):
k_sum += klist[i]
result = end - 1
while flag:
x = random.random() * k_sum
pre = 0
for i in range(0, end):
pre += klist[i]
if pre > x:
result = i
break
flag = False
# 检查结果是否在exclude_list中,如果是则重来,否则返回结果
for i in exclude_list:
if i == result:
flag = True
break
return result
# 根据BA无标度网络的规则在klist(下标为0到end 之间)中寻找m个数
# 为了简化逻辑,这里参与竞争(k!=0)的节点数必定大于m
def find(k_list, m, end):
# 结果数组
result = []
# 初始化
for i in range(0, m):
j = findOne(k_list, end, result)
# 增加结果
result.append(j)
return result
# 生成BA无标度网络,n表示点个数,m0表示初始节点数
def generateBA(n, m0, m):
global BA
# 初始BA无标度网络(利用生成器创建避免浅拷贝)
BA = [([0] * n) for i in range(n)]
# 初始化前m0个节点都为连通网络
for i in range(0, m0):
for j in range(i + 1, m0):
BA[i][j] = 1
BA[j][i] = 1
# 初始度数组
k_list = [m0 - 1] * m0 + [0] * (n - m)
# 遍历后面的节点,模拟加入
for i in range(m0, n):
# 选出m个节点
nodes = find(k_list, m, i)
for j in nodes:
BA[i][j] = 1
BA[j][i] = 1
# 更新度数组
k_list[i] += 1
k_list[j] += 1
# 对ER网络的i节点进行处理,i表示节点下标,t表示天数,b表示感染系数,y表示康复系数
def er_sir_one(i, t, b, y):
global ER, BA, ER_SIR, BA_SIR, slist, ilist, rlist
if ER_SIR[i] == 'S':
# 开始统计周围节点感染的数量
inum = 0
for x in range(len(ER_SIR)):
if (not x == i) and ER[i][x] == 1 and ER_SIR[x] == 'I':
inum += 1
# 因为是双层网络,所以BA也要考虑
if BA_SIR[i] == 'I':
inum += 1
ilist[t] += 1
p = random.random()
# 有1-(1-b)^inum概率感染
if p < 1 - (1 - b) ** inum:
ER_SIR[i] = 'I'
ilist[t] += 1
return
slist[t] += 1
elif ER_SIR[i] == 'I':
p = random.random()
# 有y的几率康复
if p < y:
ER_SIR[i] = 'R'
rlist[t] += 1
return
ilist[t] += 1
else:
rlist[t] += 1
# 对BA网络的i节点进行处理,i表示节点下标,t表示天数,b表示感染系数,y表示康复系数
def ba_sir_one(i, t, b, y):
global ER, BA, ER_SIR, BA_SIR, slist, ilist, rlist
if BA_SIR[i] == 'S':
# 开始统计周围节点感染的数量
inum = 0
for x in range(len(BA_SIR)):
if (not x == i) and BA[i][x] == 1 and BA_SIR