Leetcode刷题笔记之链表篇141. 环形链表

Posted 2022-12-06 大家好我叫张同学

😈博客主页：🐼大家好我叫张同学🐼
💖 欢迎点赞 👍 收藏 💗留言 📝 欢迎讨论！ 👀
🎵本文由 【大家好我叫张同学】 原创，首发于 CSDN 🌟🌟🌟
✨精品专栏（不定时更新） 【数据结构+算法】 【做题笔记】【C语言编程学习】
☀️ 精品文章推荐
【C语言进阶学习笔记】三、字符串函数详解（1）（爆肝吐血整理，建议收藏！！！）
【C语言基础学习笔记】+【C语言进阶学习笔记】总结篇（坚持才有收获！）

---

前言

为什么要写刷题笔记？
写博客的过程也是对自己刷题过程的梳理和总结，是一种耗时但有效的方法。
当自己分享的博客帮助到他人时，又会给自己带来额外的快乐和幸福。
（刷题的快乐+博客的快乐，简直是奖励翻倍，快乐翻倍有木有QAQ🙈）

题目内容

给你一个链表的头节点 head ，判断链表中是否有环。 如果链表中有某个节点，可以通过连续跟踪 next指针再次到达，则链表中存在环。
为了表示给定链表中的环，评测系统内部使用整数pos来表示链表尾连接到链表中的位置（索引从0 开始）。如果pos 是-1，则在该链表中没有环。
注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。 如果链表中存在环，则返回 true 。 否则，返回 false 。

原题链接（点击跳转）

暴力取巧法

要解决这个问题，有一个不算方法的方法，我们注意到题目中说了链表中节点的数目范围是[0, 10^4]。
对于带环的链表，我们去求其长度，一定是大于10^4的（也就是10000）。
对于不带环的链表，其长度一定是小于等于10000的。因此这个地方可以取巧，直接取计算链表的长度，就可以判断是否带环。

函数实现

bool hasCycle(struct ListNode *head) 
    //暴力求解法 如果链表有环，长度计算length会无穷大
    struct ListNode* cur = head;
    int length = 0;
    while(cur && (length < 100001)) 
        cur = cur->next;
        length++;
    
    if(cur == NULL)
        return false;
    else
        return true;

虽然这种方法可以求出链表是否带环，但实际中我们最好不要使用这种方法。
原因如下：

1）这种方式需要事先知道链表的最大长度是多少。
2）当链表长度很大的时候，比如1千万、1个亿结点，这时候程序的效率就会很低。

---

快慢指针法

要判断链表是否带环，一般都采用快慢指针的方法（快指针一次走两步，慢指针一次走一步）。若链表不带环，那么快指针势必会走到最后一个结点或空结点，即fast = NULL，或 fast->next = NULL。若链表不带环，那么快指针后面就会一直在环里面走啊走，转啊转，出不去。若while循环中终止条件是fast == NULL或 fast->next == NULL,那么while循环就无法终止。为了在链表带环时，while循环还能终止，将条件改为 fast != slow。若带环，则fast与slow必定会在环中相遇。（证明过程在后面）

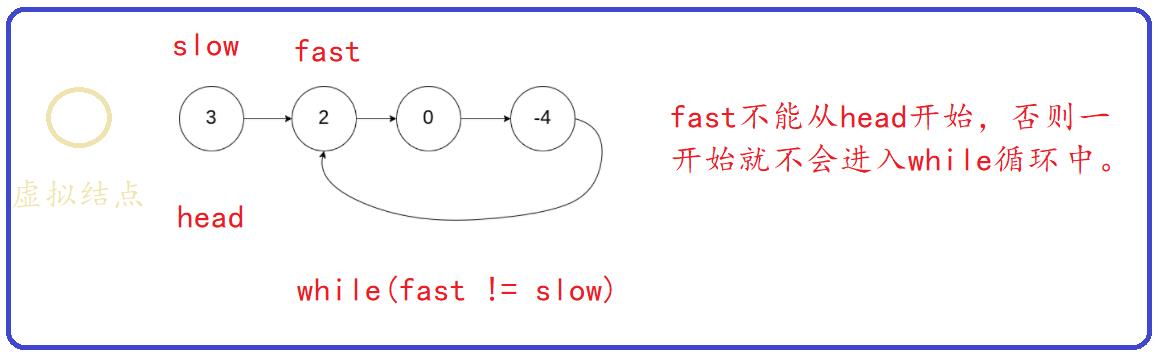
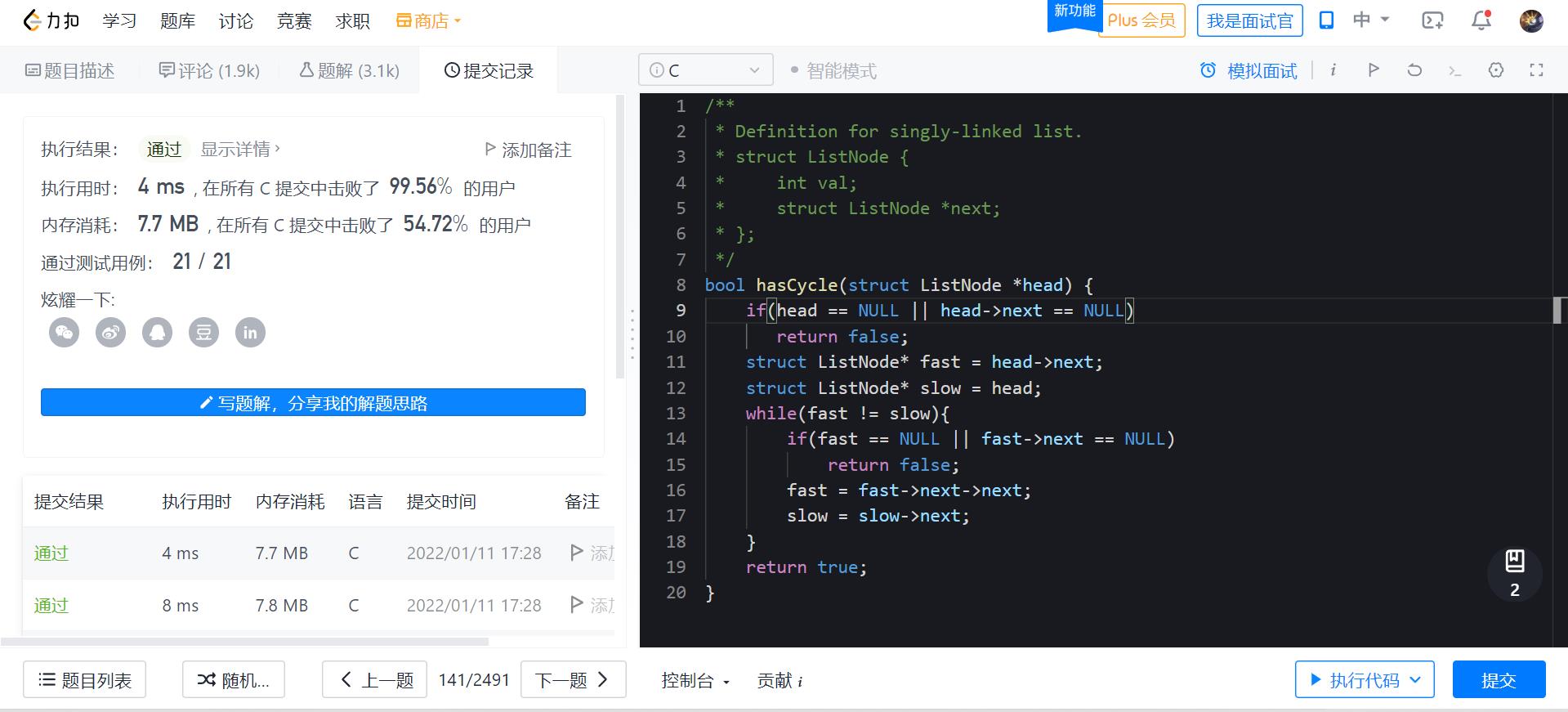
函数实现

bool hasCycle(struct ListNode *head) 
    if(head == NULL || head->next == NULL)
       return false;
    struct ListNode* fast = head->next;
    struct ListNode* slow = head;
    while(fast != slow)
        if(fast == NULL || fast->next == NULL)
            return false;
        fast = fast->next->next;
        slow = slow->next;
    
    return true;

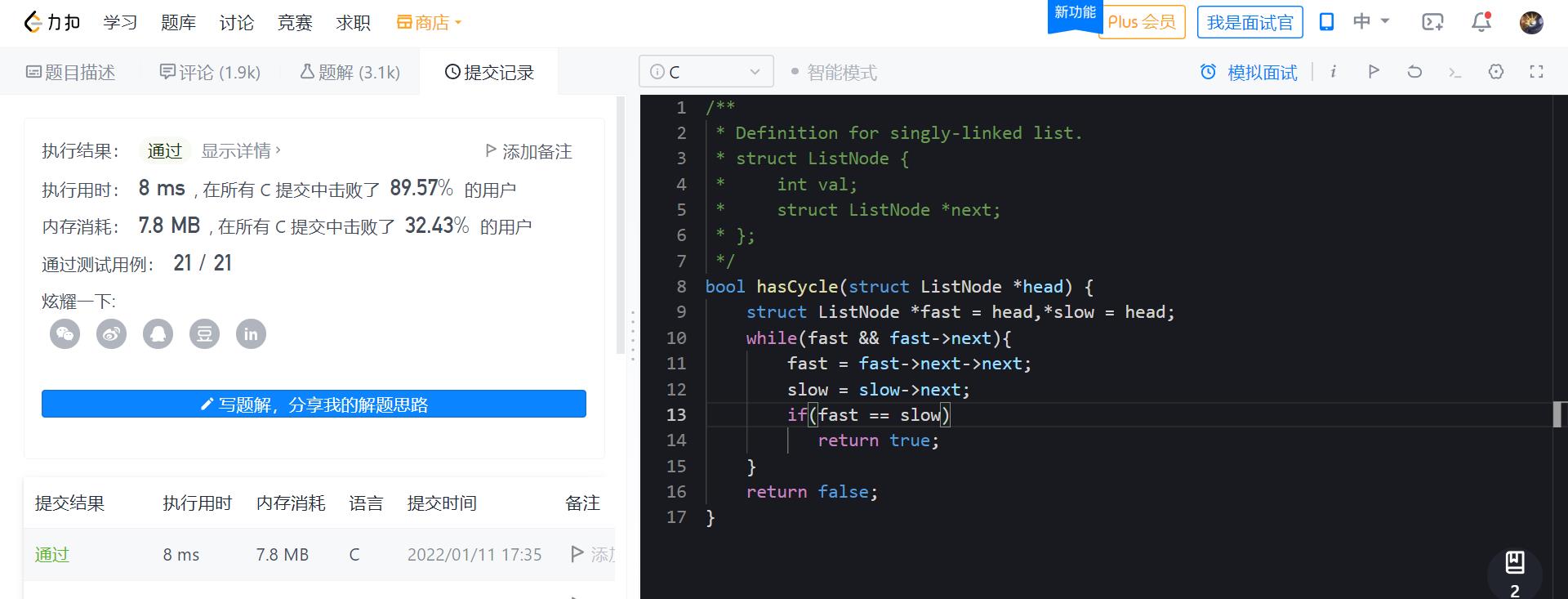
当然也可以这样写，这样就不需要利用虚拟结点，fast和slow同时从头结点head开始往后走。

bool hasCycle(struct ListNode *head) 
    struct ListNode *fast = head,*slow = head;
    while(fast && fast->next)
        fast = fast->next->next;
        slow = slow->next;
        if(fast == slow)
           return true;
    
    return false;

---

带环问题的证明过程

这种证明问题在面试的时候经常会被问道，一般会从下面两个角度来提问：

1）slow一次走一步，fast一次走两步，一定可以相遇吗？请证明
2）slow一次走一步，fast一次走n步（n >2，n = 3，4，5…），一定可以相遇吗？请证明

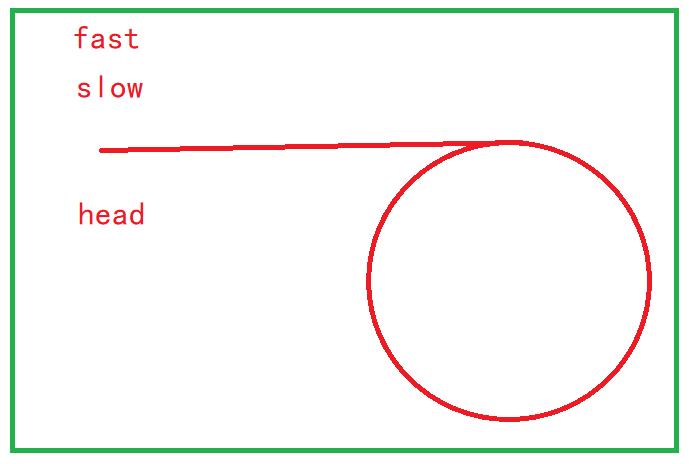
问题（1）
答：一定可以追上，证明如下：

①首先我们要理解环的大小、环前面链表部分的长度都是不确定的。
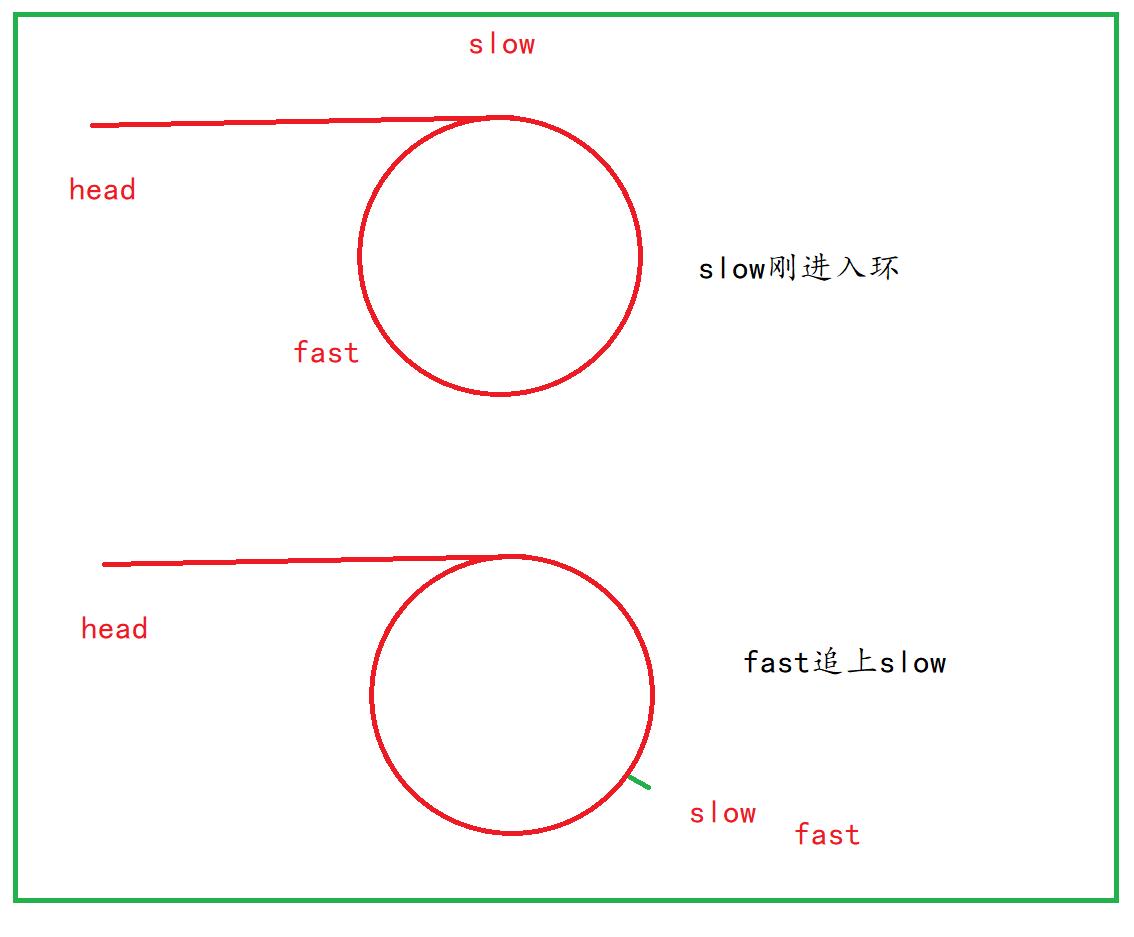
②那么当slow进入环的时候，fast已经在环里面走了一会了，这时候fast要和slow相遇，就需要fast追上slow。
③假设slow进入环的时候，fast和slow之间的距离为n（fast追上slow需要的步数），环的大小为c，那么n一定小于c（如果n == c或 n == 0，两者就相遇了)。
④而fast在追赶slow的过程中，slow一次走一步，fast一次走两步，则fast和slow之间的距离就会减少1，最终n变为0 ，所以fast一定可以追上slow。
⑤slow进入环里面后，一圈之内，fast一定会追上slow，也就是fast不会错过slow。

问题（2）
答：不一定可以追上，证明如下：

①假设slow一次走一步，fast一次走三步，slow进环时，它们之间的差距为n，环的长度为c。
②fast在追赶slow的过程中，slow一次走一步，fast一次走三步，则fast和slow之间的距离就会减少2。也就是说距离会变成n-2、n-4、n-6....，当n为偶数的时候，fast就一定可以追上slow，当n为奇数的时候，且c - 1也为奇数时，fast就永远追不上slow，一直错过。
③n为奇数的时候，n-2、n-4、n-6.... 最后变为-1，-1就是表示fast与slow相差-1步，也就是c-1步。当c-1为偶数，那么fast还是可以追上slow。当c-1为奇数，fast永远追不上slow。