标准单元库(上)

Posted 2022-12-05 KuoGavin

文章目录

• • 3.1 引脚电容(Pin Capacitance)
  • 3.2 时序模型(Timing Modeling)
  • • 3.2.1 线性时序模型(Linear Timing Model)
    • 3.2.2 非线性时序模型(Non-linear Timing Model)
    • 3.2.3 阈值规格和压摆降额(Threshold Specifications and Slew Derating)
  • 3.3 时序模型-组合逻辑单元(Timing Model-Combinational Logic Cells)
  • • 3.3.1 时延和压摆模型(Delay and Slew Models)
    • 3.3.2 通用组合逻辑块(General Combinational Block)
  • 3.4 时序模型-序列逻辑单元(Timing Models-Sequential Cells)
  • • 3.4.1 同步检查：建立和保持(Synchronous Check: Setup and Hold)
    • 3.4.2 异步时序检查(Asynchronous Checks)
    • 3.4.3 传播时延(Propagation Delay)
  • 知乎翻译圣经

---

本章介绍库（library）里单元描述中所提供的时序信息。单元可以是标准单元、IO缓冲器或者是如USB内核这样的复杂IP。

• 除时序信息外，库单元描述中还包含一些其它属性，例如单元面积和功能，这些属性与时序无关，但在RTL综合（synthesis）过程中会用到。在本章中，我们仅关注与时序和功耗计算有关的那些属性。
• 可以使用各种标准格式来描述库单元，各种格式的内容基本相似，本书中使用Liberty语法描述库单元。
• 本章前面部分介绍了线性和非线性时序模型，随后介绍了用于纳米技术的高级时序模型，这些将在3.7节中进行介绍。

---

---

3.1 引脚电容(Pin Capacitance)

单元的每个输入和输出都可以在引脚（pin）上指定电容。在大多数情况下，仅为单元输入引脚指定电容，而不为输出引脚指定电容，即大多数单元库中的输出引脚电容为0。

pin(INP1) 
	capacitance:0.5;
	rise_capacitance:0.5;
	rise_capacitance_range:(0.48, 0.52);
	fall_capacitance:0.45;
	fall_capacitance_range:(0.435, 0.46);
	...

上面的示例展示了输入INP1引脚电容值的一般规格（specification）。在最基本的格式中，引脚电容被指定为单个值（在上面的示例中为0.5个单位）。电容单位通常为皮法拉（pF），一般在库文件的开头指定。单元描述中还可以为rise_capacitance（0.5个单位）和fall_capacitance（0.45个单位）分别指定值，这些值是指引脚INP1上发生电平上升和下降转换(transition)时的值。也可以将rise_capacitance和fall_capacitance的值指定为范围，并在描述中指定下限值和上限值。

---

---

3.2 时序模型(Timing Modeling)

逻辑单元的时序模型（timing model）旨在为设计中的各种单元实例（instance）提供准确的时序信息。通常会从单元的详细电路仿真中获得时序模型，用以对单元工作时的实际情况进行建模，且需要为逻辑单元的每个时序弧都建立一个时序模型。

先来考虑简单逻辑单元反相器的时序弧，如下图，其中其输入引脚的上升(下降)沿造成输出针脚的下降(上升)沿。这两种时延分别对应于$T_f$(output fall delay)和$T_r$(output rise delay)。

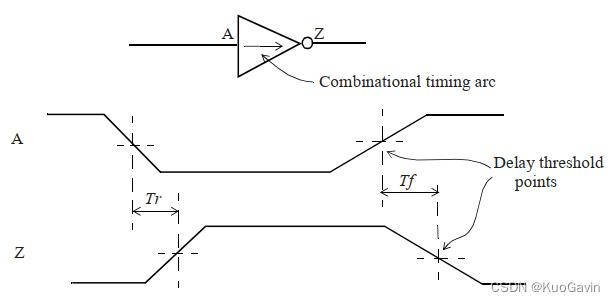
注意，延迟是根据单元库中定义的阈值（threshold）点测量的，通常为50％$V_{dd}$。 因此，延迟值指从输入经过其阈值点到输出经过其阈值点的延迟。

通过反相器的时序弧的延迟取决于两个因素：

• 输出负载，即反向器输出针脚上的电容负载；
• 输入信号的过渡时间(transition time)；

延迟值与负载电容有单调关系：负载电容$\uparrow$，延迟值$\uparrow$；

延迟值与过渡时间的关系不定：多数情况下，过渡时间$\uparrow$，延迟值$\uparrow$；某些情况下，输入信号阈值点(用于测量延迟)与单元的内部开关点(switching point)明显不同，此时通过单元的延迟可能相对于输入信号过渡时间表现出非单调行为：过渡时间$\uparrow$，延迟值$\downarrow$，尤其负载电容值较小的情况下。

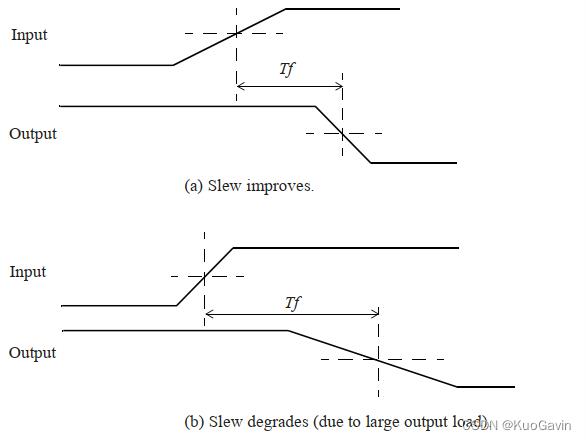
逻辑单元输出引脚的压摆(slew)主要取决于输出引脚的输出电容：输出信号过渡时间会随着输出负载的增加而增加。因此，在输入端压摆时间(压摆是模电中概念，过渡时间是数电中概念)较大(过渡时间较长，理解即可不必纠结)情况下，选择合适的单元类型及输出负载，可以改善输出端的压摆。如下图所示，(b)由于更大的负载，所以压摆就很大。

---

3.2.1 线性时序模型(Linear Timing Model)

一个简单的时序模型是线性延迟模型（linear delay model），该模型使用含两个参数的线性函数表示逻辑单元的延迟和输出过渡时间，这两个参数是：输入过渡时间（input transition time）和输出负载电容（output load capacitance）。通过逻辑单元的延迟（$D$）使用线性模型的一般形式如下所示：
$$D=D_0+D_1\ast S+D_2\ast C$$
其中$D_0$，$D_1$，$D_2$是常数，$S$是输入过渡时间，$C$是输出负载电容。 对于亚微米（submicron）技术，线性延迟模型在输入过渡时间和输出负载电容的范围内并不准确，因此，目前大多数单元库都使用更复杂的模型，例如非线性延迟模型（non-linear delay model）。

---

3.2.2 非线性时序模型(Non-linear Timing Model)

大多数单元库都包括表格模型（table model），用于为单元的各种时序弧指定延迟并进行时序检查。一些用于纳米技术的较新的时序库还提供了基于电流源的高级时序模型（例如CCS，ECSM等），本章稍后将对此进行介绍。 这些表格模型被称为NLDM（Non-Linear Delay Model），可用于延迟、输出压摆计算或其他时序检查。表格模型中提供了：在单元输入引脚处输入过渡时间和输出引脚处输出负载电容的各种组合下通过单元的延迟。

NLDM模型以二维形式表示，两个独立变量是输入过渡时间和输出负载电容，表中的数值表示延迟。以下是一个典型反相器单元的表格模型示例：

pin (OUT) 
	max_transition : 1.0;
	timing() 
		related_pin : "INP1";
		timing_sense : negative_unate;
		cell_rise(delay_template_3x3) 
			index_1 ("0.1, 0.3, 0.7"); /* Input transition */
			index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
			values ( /* 0.16 0.35 1.43 */ \\
			/* 0.1 */ "0.0513, 0.1537, 0.5280", \\
			/* 0.3 */ "0.1018, 0.2327, 0.6476", \\
			/* 0.7 */ "0.1334, 0.2973, 0.7252");
		
		cell_fall(delay_template_3x3) 
			index_1 ("0.1, 0.3, 0.7"); /* Input transition */
			index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
			values ( /* 0.16 0.35 1.43 */ \\
			/* 0.1 */ "0.0617, 0.1537, 0.5280", \\
			/* 0.3 */ "0.0918, 0.2027, 0.5676", \\
			/* 0.7 */ "0.1034, 0.2273, 0.6452");
		

上面的示例描述了输出引脚OUT的延迟信息。单元描述里的这个部分包含了从引脚INP1到引脚OUT时序弧的上升和下降延迟模型，以及引脚OUT的max_transition允许时间。上升和下降延迟有单独的模型(models)（用于输出引脚），分别标记为cell_rise和cell_fall。索引（indices） 变量的类型和顺序在以下查找表模板（lookup table template）delay_template_3x3中进行了描述：

lu_table_template(delay_template_3x3) 
	variable_1 : input_net_transition;
	variable_2 : total_output_net_capacitance;
	index_1 ("1000, 1001, 1002"); 	//index_1 ("0.1, 0.3, 0.7");
	index_2 ("1000, 1001, 1002");	//index_2 ("0.16, 0.35, 1.43");
	//the above data such as 1000 is dummy placeholder.
	//the annonated data is the actual data can be altered in 
	//models or just be specified in template table.
/* The input transition and the output capacitance can be
in either order, that is, variable_1 can be the output
capacitance. However, these designations are usually
consistent across all templates in a library. */

可以当作for循环嵌套，index_1(输入过渡时间)和index_2(总输出网络电容，即输出负载电容)均有三个可能值，所以对应的应当是$3\times 3$的表格。对于表格索引值的设定，可以通过两种方法：

• 上述模板表中索引值(e.g. 1000)是伪占位符(dummy placeholder)，可在cell_fall或cell_rise延迟表中实际索引值进行覆盖；
• 在模板定义中指定索引值，类似于默认值的设定；

根据延迟表，输入下降过渡时间为0.3ns且输出负载为0.16pf时，反相器的上升延迟为0.1018ns。 由于输入的下降沿跳变导致反相器输出的上升沿跳变，因此当输入引脚发生下降沿跳变时，应该去查询cell_rise延迟表。

将表格中的延迟值表示为输入过渡时间和输出负载电容这两个变量的函数的这种形式称为非线性延迟模型，因为在这些表格中可以看到延迟随输入过渡时间和输出负载电容的非线性变化。

注意，表格模型也可以是3维的，例如一个具有互补输出Q和QN的触发器，这将在3.8节中进行介绍。

NLDM模型不仅可以用于计算延迟，而且还可用于计算逻辑单元输出引脚的过渡时间，该时间同样由输入过渡时间和输出负载电容来表征。因此，还存在着另外一张独立的用于计算单元的输出上升和下降过渡时间的二维表格。

pin (OUT) 
	max_transition : 1.0;
	timing() 
		related_pin : "INP";
		timing_sense : negative_unate;
		rise_transition(delay_template_3x3) 
			index_1 ("0.1, 0.3, 0.7"); /* Input transition */
			index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
			values ( /* 0.16 0.35 1.43 */ \\
			/* 0.1 */ "0.0417, 0.1337, 0.4680", \\
			/* 0.3 */ "0.0718, 0.1827, 0.5676", \\
			/* 0.7 */ "0.1034, 0.2173, 0.6452");
		
		fall_transition(delay_template_3x3) 
			index_1 ("0.1, 0.3, 0.7"); /* Input transition */
			index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
			values ( /* 0.16 0.35 1.43 */ \\
			/* 0.1 */ "0.0817, 0.1937, 0.7280", \\
			/* 0.3 */ "0.1018, 0.2327, 0.7676", \\
			/* 0.7 */ "0.1334, 0.2973, 0.8452");
		
		. . .
	
	. . .

这里有两个关于过渡时间的表格：rise_transition和fall_transition。如第二章所述，过渡时间是根据特定的压摆阈值点(通常为电源的10%-90%)测量的。

综上所述，使用NLDM模型的反相器具有下列表格模型：

• Rise delay (上升延迟时间)
• Fall delay (下降延迟时间)
• Rise transition (上升过渡时间)
• Fall transition (下降过渡时间)

假设有这么一个反相器单元，其输入过渡时间和输出负载电容如下图所示。对于15ps的输入（下降）过渡时间和10fF负载，可从cell_rise表中获得输出上升延迟时间，而从cell_fall表中可获得20ps输入（上升）过渡时间和10fF负载下的输出下降延迟时间 。

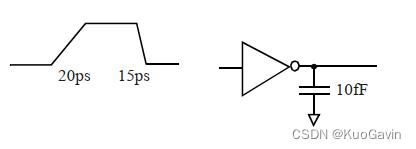
指定单元逻辑功能为“反相”（invert）的信息可以在时序弧里的timing_sense字段中找到，但在某些情况下如果该字段中未指明，则应该也可从引脚功能（pin function）中推断出。

例如对于反相器单元，时序弧为negative_unate，这表明输出引脚电平跳变方向与输入引脚电平跳变方向相反。因此，在cell_rise表中进行查找时使用的参数是输入引脚的下降过渡时间。

对于未在表中出现的对应的(input transition, out capacitance)对，它们的输出延迟值由二维插值进行求取以得到最终的时序值，一般选择每个维度中两个最接近的表格条目的值进行表格插值。考虑(0.15, 1.16pF)的输出下降时延值，下面从下降时延表格中复制了与二维插值相关的部分：

fall_transition(delay_template_3x3) 
	index_1 ("0.1, 0.3 . . .");
	index_2 (". . . 0.35, 1.43");
	values ( \\
	". . . 0.1937, 0.7280", \\
	". . . 0.2327, 0.7676"
	. . .

在插值的计算公式中，$inde{x}_1$的两个插值值标记为$x_1$和$x_2$；$inde{x}_2$的两个插值值标记为$y_1$和$y_2$，这些插值值对应的表格中的数值记为$T_{11}$，$T_{12}$，$T_{21}$和$T_{22}$。若是所需查找的表中值的行列值为$(x_0,y_0)$，那么所查值$T_{00}$的插值公式如下：
$$\begin{gathered} T_{00}=x_{20}\ast y_{20}\ast T_{11}+x_{20}\ast y_{01}\ast T_{12}+ \\ {x}_{01}\ast y_{20}\ast T_{21}+x_{01}\ast y_{01}\ast T_{22} \end{gathered}$$
其中：
x 01 = ( x 0 − x 1 ) / ( x 2 − x 1 ) x 20