高精度运算（除法待完善）

Posted 2022-12-05 东条希尔薇

我们知道，在c语言中，数据的存储是有范围的，超出了这个范围的数据将不能有效的进行存储和运算

而超出c语言储存范围的数，不能用c语言基本数据类型储存的数据，就叫做大数

所以，为了解决大数的运算问题，我们来介绍一下如何在c语言中实现大数运算

大数加减法

首先介绍最基本的大数加减法

这篇文章中我们把任意小于200位的非负整数的数都称作大数

例如：88888888888888888888,123456789987654321

而我们要储存这么大的数字，只能用一个字符数组来储存

char a[200]=0;
char b[200]=0;

例如，我们要存储123456789这个数字，在内存中只能这么储存

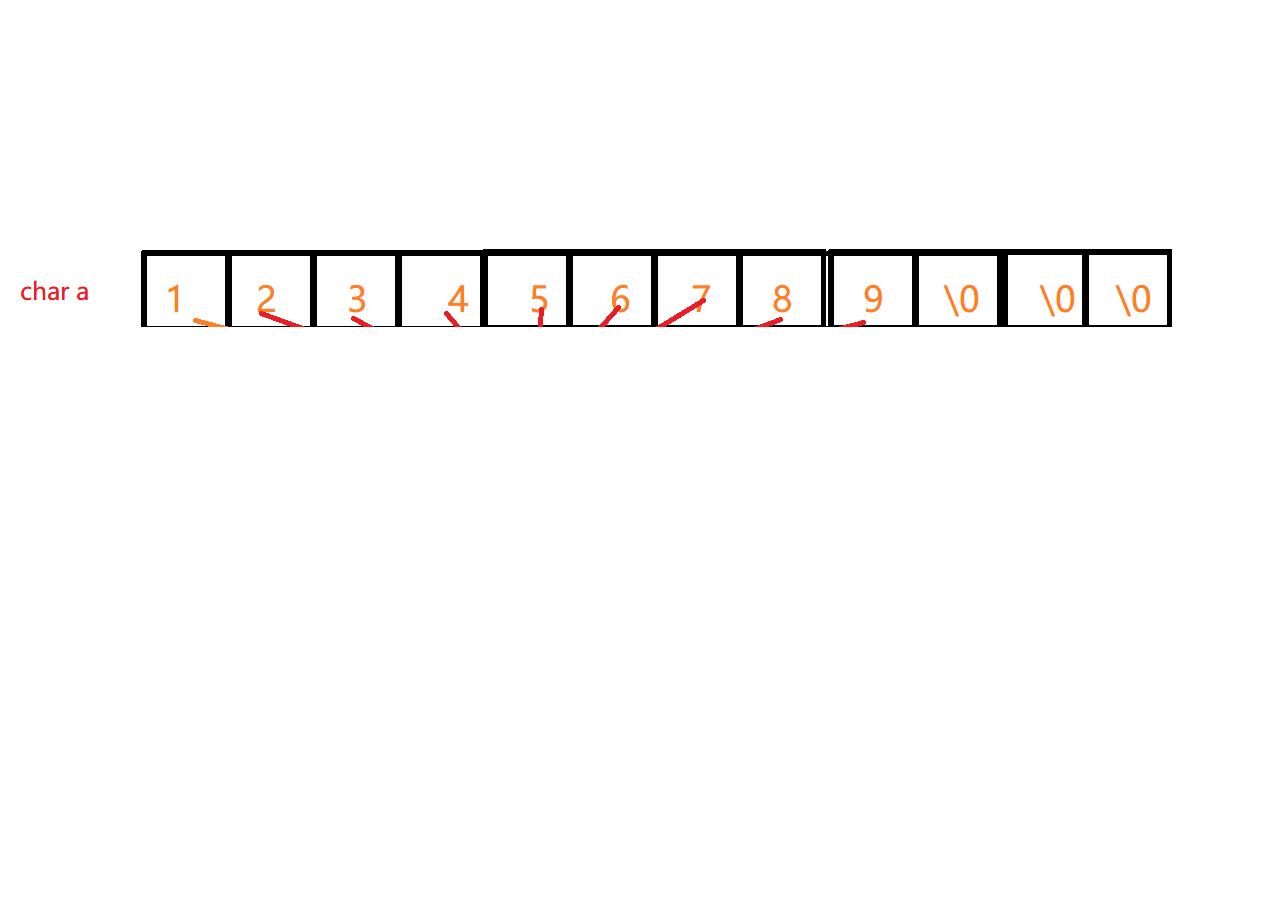
但我们在两个数字进行运算的时候，当遇到进位的时候，需要将所有数字往后移动一位，为了避免这种麻烦，也为了能方便控制下标

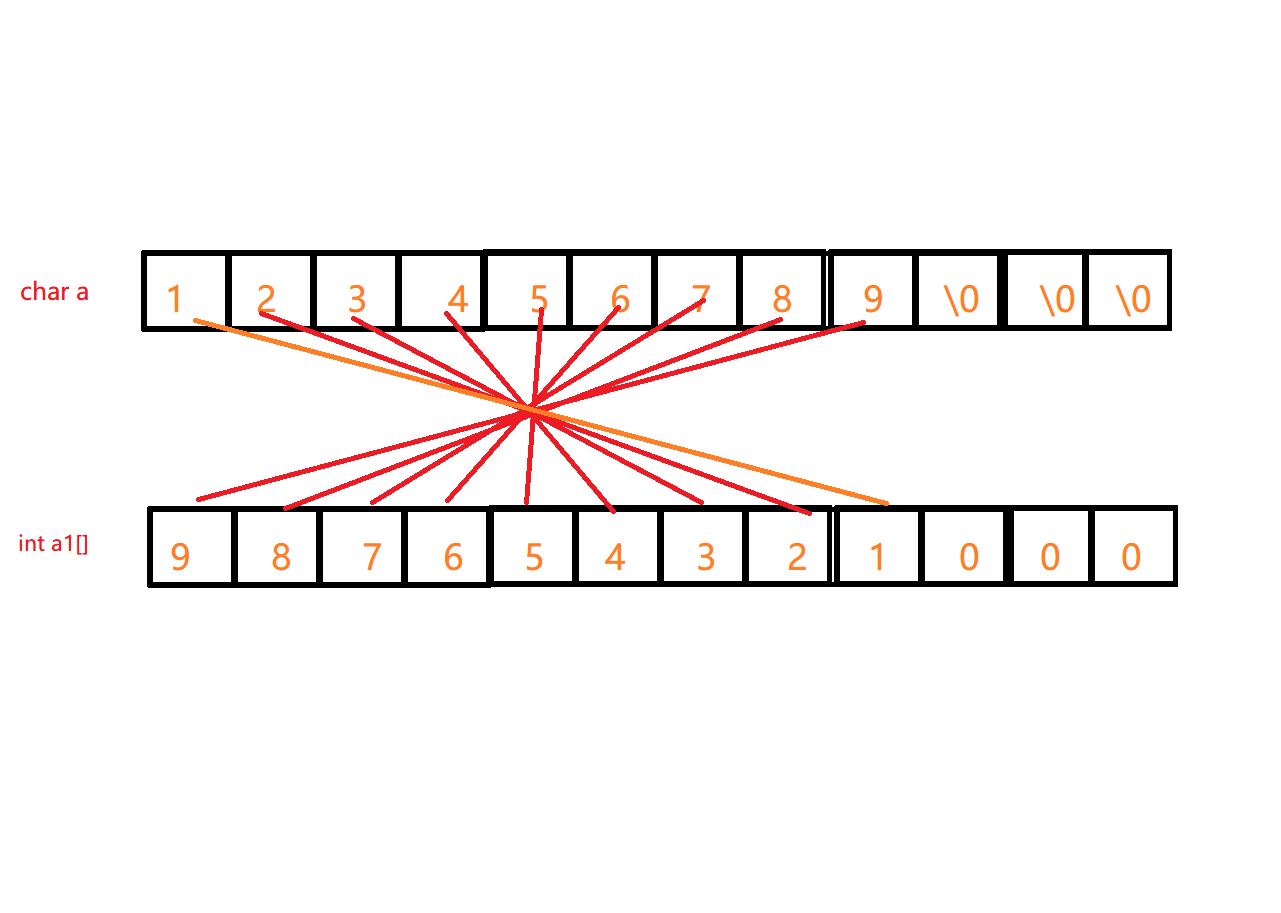
所以我们在运算中需要将数字倒过来存储，并将其存储至另外一个整数数组中

int a1[200]=0;
int b1[200]=0;

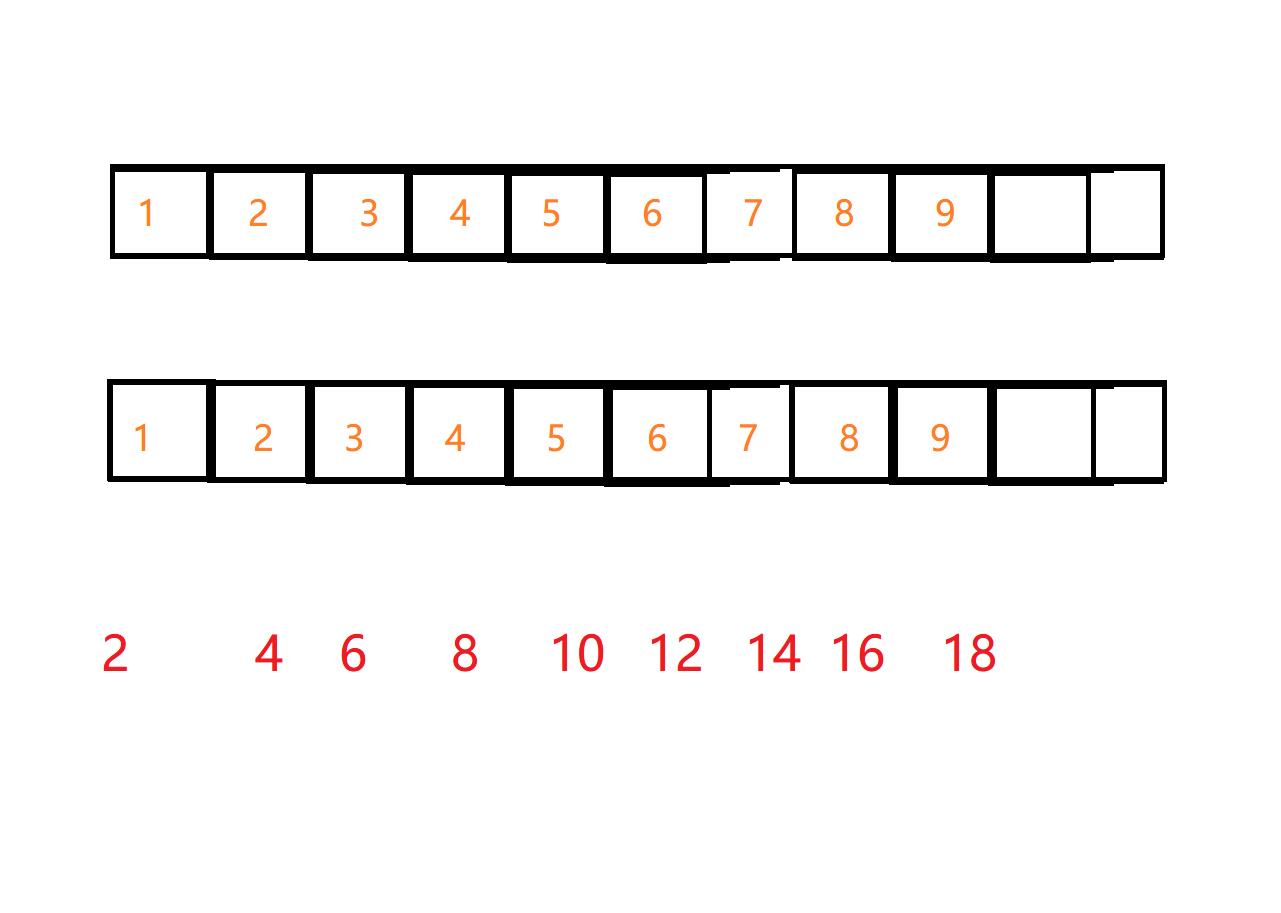
存储方式如下

	int len_a = strlen(a);
	int len_b = strlen(b);//先求出两个数字的位数
	int i = 0;
	for (i = 0; i < len_a; i++)
	
		a1[len_a - 1 - i] = a[i] - '0';
	

	for (i = 0; i < len_b; i++)
	
		b1[len_b - 1 - i] = b[i] - '0';
	//为运算做准备

接下来就要进行运算了,运算结果为了表示方便，运算结果同样存储在一个整型数组中保存

运算就可以一位一位的进行运算，但也需要先确定和运算的位数

int len = len_a > len_b ? len_a : len_b;//求和用的长度
sum[i] = a1[i] + b1[i]

但是加法，我们必须要考虑进位的情况

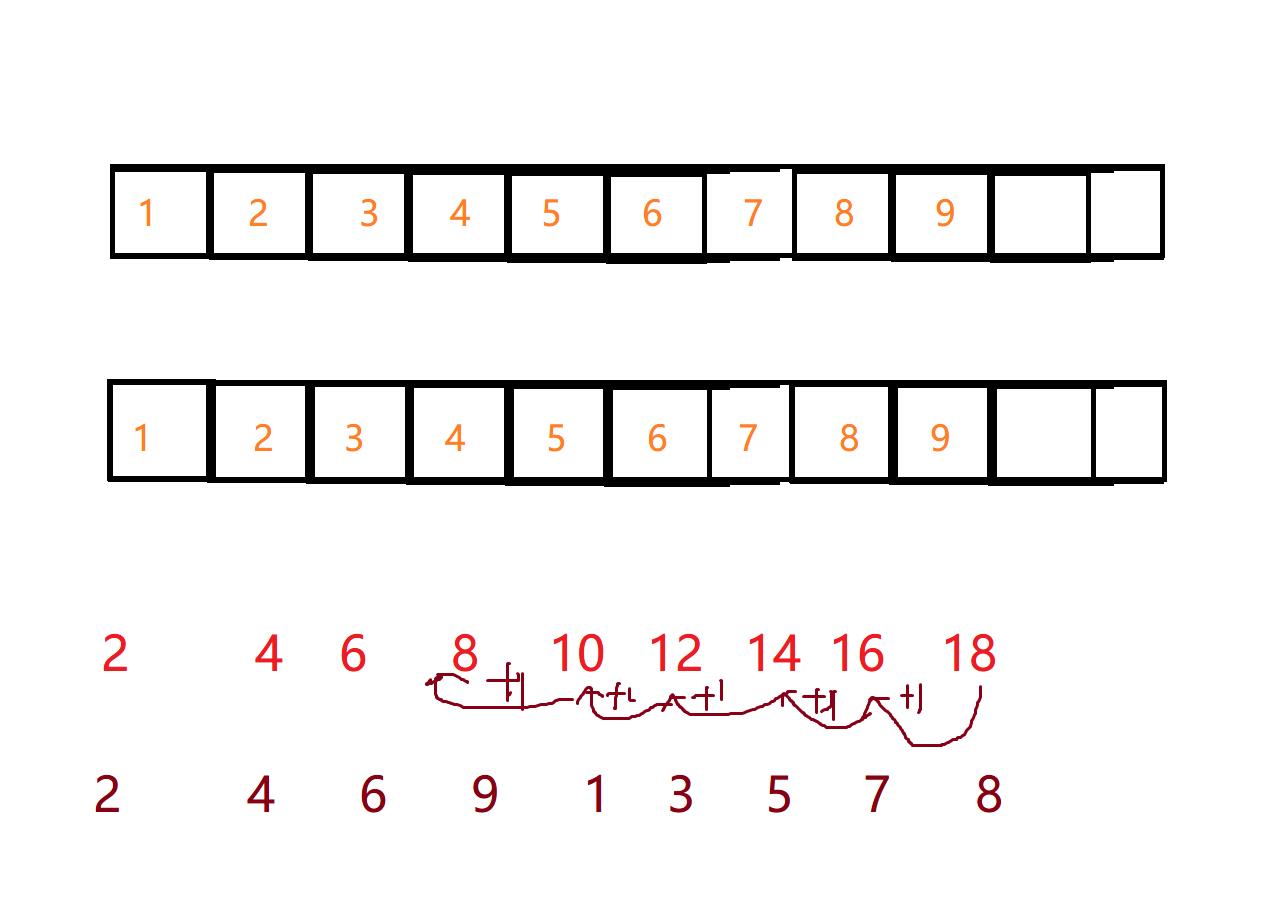
我们在运算中有一些位数运算结果已经大于10了，代表需要进行进位

我们可以用一个临时变量d保存我们的进位信息

某一位数大于10，就代表我们需要进位了

• 用/提取第一位数字，也就是进位数

• 用%提取最后位数字，也就是此位数

提取到的进位数，就需要加在下一次位数运算中，就这样算一位就马上将进位数保存，加在下一次运算中

也就像这样

sum[i] = a1[i] + b1[i] + d;

但还有一种情况，在最高位进位的情况

只需要在运算完成后，检查进位数是否为0，若不为0，则进位并把结果总位数加一

完整代码实现

int main()

	char a[200] =  0 ;
	char b[200] =  0 ;//保存求和的两个大数
	int a1[200] =  0 ;
	int b1[200] =  0 ;//进行运算的临时数组
	int sum[201] =  0 ;//存放和的数组，由于进位需要多一位
	char out_sum[201] =  0 ;//需要表示大数和的字符串
	scanf("%s", a);
	scanf("%s", b);//读入两个大数
	int len_a = strlen(a);
	int len_b = strlen(b);
	int i = 0;
	for (i = 0; i < len_a; i++)
	
		a1[len_a - 1 - i] = a[i] - '0';
	

	for (i = 0; i < len_b; i++)
	
		b1[len_b - 1 - i] = b[i] - '0';
	//为运算做准备
	
	int len = len_a > len_b ? len_a : len_b;//求和用的长度

	int d = 0;//保存进位结果
	for (i = 0; i < len; i++)
	
		sum[i] = a1[i] + b1[i] + d;
		if (sum[i] > 10)
		
			d = sum[i] / 10;//算进位
			sum[i] %= 10;//算余数

		
		else
			d = 0;//没有进位则需要将进位重置

	

	if (d > 0)
	
		sum[len] += d;
		len++;
	//最高位需要进位的情况
	
	for (i = 0; i < len; i++)
	
		out_sum[i] = sum[len -1 - i] + '0';
	
	
	for (i = 0; i < len; i++)
	
		printf("%c", out_sum[i]);
	
	return 0;

测试用例

大数乘法

这里的大数指的是小于50位的非负整数

其存储方式的思想和大数加法的思想差不多

主要讲一下大数乘法的运算

类比于手算，我们也需要一位一位的进行运算，同样先不考虑进位，待所有位运算完成后统一进行

通过对乘法的理解我们发现：

i位和j位的运算结果放在i+j位中

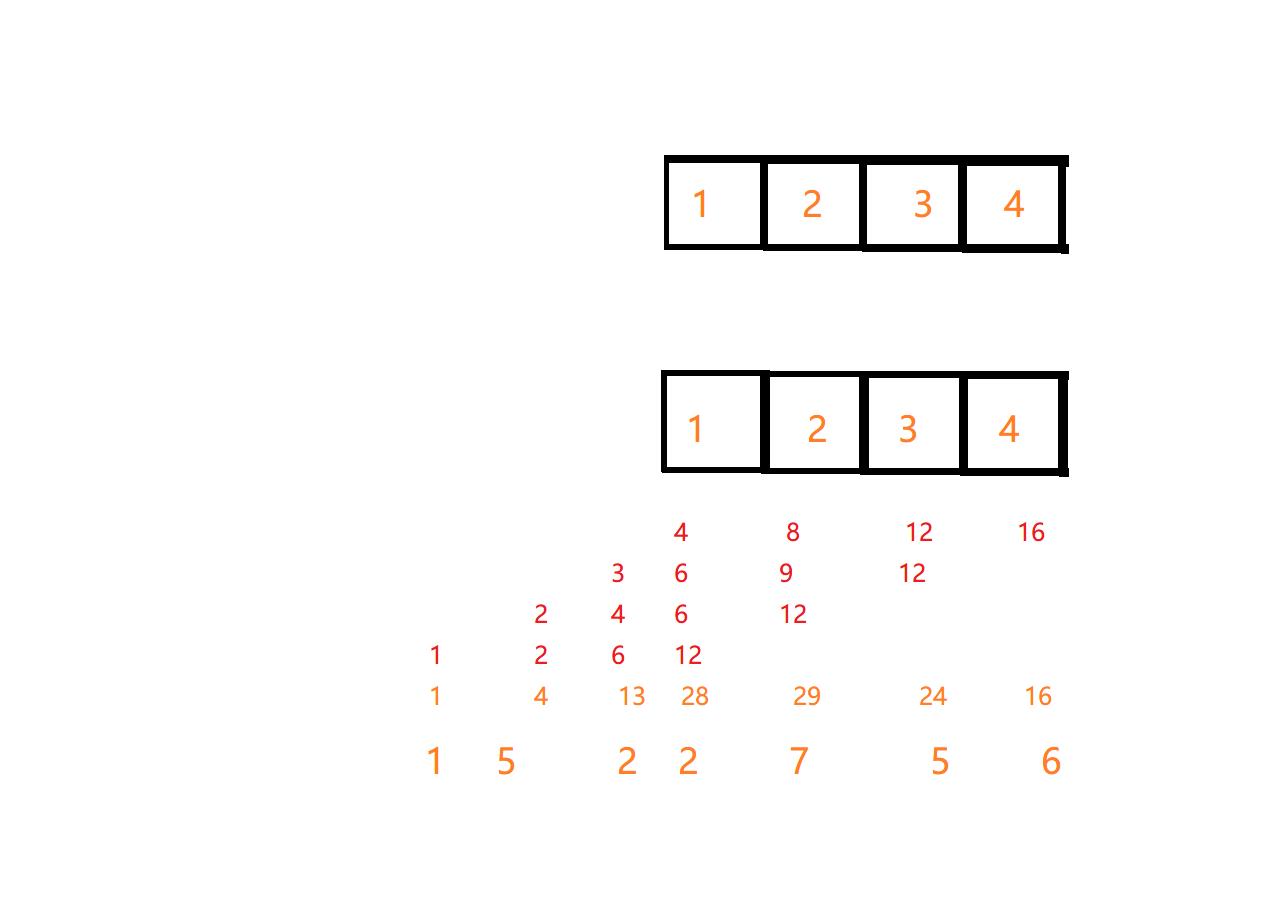
for (i = 0; i < len_a; i++)
	
		
		for (j = 0; j < len_b; j++)
		
			pow[i + j] += a1[i] * b1[j];
		
	

而进位，则在最后进行，方法可以参考大数加法

int count = i + j - 1;//找到结果的最大位

	int d = 0;
	for (i = 0; i < count; i++)
	
		pow[i] += d;
		if (pow[i] > 10)
		
			d = pow[i] / 10;
			pow[i] %= 10;
		
		else
		
			d = 0;
		
	
	if (d > 0)
	
		pow[count] += d;
		count++;
	

完整代码实现

int main()

	char a[50] =  0 ;
	char b[50] =  0 ;
	int a1[50] =  0 ;
	int b1[50] =  0 ;
	int pow[100] =  0 ;
	char out_pow[100] =  0 ;
	scanf("%s", a);
	scanf("%s", b);
	int i = 0;
	int len_a = strlen(a);
	int len_b = strlen(b);

	
	for (i = 0; i < len_a; i++)
	
		a1[len_a - 1 - i] = a[i] - '0';
	

	for (i = 0; i < len_b; i++)
	
		b1[len_b - 1 - i] = b[i] - '0';
	
	int j = 0;
	for (i = 0; i < len_a; i++)
	
		
		for (j = 0; j < len_b; j++)
		
			pow[i + j] += a1[i] * b1[j];
		
	

	int count = i + j - 1;

	int d = 0;
	for (i = 0; i < count; i++)
	
		pow[i] += d;
		if (pow[i] > 10)
		
			d = pow[i] / 10;
			pow[i] %= 10;
		
		else
		
			d = 0;
		
	
	if (d > 0)
	
		pow[count] += d;
		count++;
	

	for (i = 0; i < count; i++)
	
		out_pow[i] = pow[count -1 - i] + '0';
	
	
	for (i = 0; i < count; i++)
	
		printf("%c", out_pow[i]);
	
	return 0;

测试：

大数除法

这里的大数指的是小于100位的非负整数

并且，除法运算做的是int类型的运算，也就是运算结果中没有小数点

前面的大数加法，乘法都是模拟的手工运算

但大数除法直接手算模拟却非常麻烦，因为除法不能一位一位的进行运算

所以我们必须要模拟大数减法进行实现

基本思想：反复做减法，看看被除数能减除数多少次

例如7546除以23中，7546能被23减去328次，所以最后结果是328

但这么一次次的减，效率显然比较低，为了提高程序的效率，我们可以先将除数位数升高到与被除数相同，再进行减法运算，可大大减少运算次数

• 上面的算式中，先把23提升到2300,7546能被2300减去3次，所以商的值增加300

• 减完后剩下646，先把23提升到230,646能被230减去2次，所以商的值增加20

以此类推。。。

但这个代码中，需要先实现一个大数减法的功能,再进行运算

int Subtract(int* a1, int* b1, int len_a, int len_b, int* sub)

	int i = 0;
	if (len_a < len_b)
		return -1;
	else if (len_a == len_b)
	
		for (i = len_a - 1; i >= 0; i++)
		
			if (a1[i] < b1[i])
				return -1;
		
	//首先判断被减数是否比减数大
	int d = 0;
	for (i = 0; i < len_a; i++)
	
		sub[i] = a1[i] - b1[i] + d;
		if (sub[i] < 0)
		
			sub[i] += 10;
			d = -1;
		
		else
		
			d = 0;
		//涉及到了借位
	
	for (i = len_a - 1; i >= 0; i++)
	
		if (sub[i])
			return i + 1;//返回结果的位数
	
	return 0;