Java数据结构与算法解析——二叉查找树

Posted 2022-12-05 4K_WarCraft

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Java数据结构与算法解析——二叉查找树相关的知识，希望对你有一定的参考价值。

二叉查找树简介

二叉查找树(Binary Search Tree)，又被称为二叉搜索树。
它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：

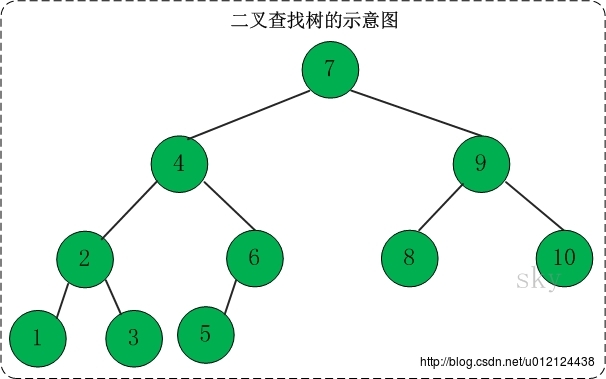
在二叉查找树中：
(1) 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
(2) 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
(3) 任意节点的左、右子树也分别为二叉查找树。
(4) 没有键值相等的节点（no duplicate nodes）。

二叉查找树的实现

1.二叉查找树节点实现

public class BinaryNode<T> 
    private T element;
    private BinaryNode<T> left;
    private BinaryNode<T> right;

    public BinaryNode(T element, BinaryNode<T> left, BinaryNode<T> right) 
        this.element = element;
        this.left = left;
        this.right = right;
    

    public BinaryNode(T element) 
        this(element, null, null);
    


 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

(1) element–当前节点的值
(2) right – 它指向当前节点的右孩子。
(3) parent – 它指向当前节点的父结点。

2.contains方法的实现

如果在树T中存在含有项X的节点，那么contains方法返回true,否则返回false.如果树T是空集，则返回false.

public boolean contains(T t, BinaryNode<T> node) 
        if (t == null) 
            return false;
        

        int campareResult = t.compareTo(node.element);
        if (campareResult < 0) 
            return contains(t, node.left);
         else if (campareResult > 0) 
            return contains(t, node.right);
         else 
            return true;
        
    

 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

从根节点开始查找该值，如果根节点匹配，则直接返回true,否则和根节点的值进行比较，然后递归遍历左子树或右子树进行查找。

3.findMin方法和findMax方法

 public T findMax() 
        if (isEmpty()) 
            throw new IndexOutOfBoundsException();
        
        return findMax(mRoot).element;
    

    private BinaryNode<T> findMax(BinaryNode<T> node) 
        if (node != null) 
            while (node.right != null) 
                node = node.right;
            
        
        return node;
    
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

对于findMax方法，如果存在右子树，则递归遍历，终止点就是最大的元素。否则，根节点就是最大的元素。

 public T findMin()
        if (isEmpty()) 
            throw new IndexOutOfBoundsException();
        
        return findMin(mRoot).element;
    

    private BinaryNode<T> findMin(BinaryNode<T> node) 
        if (node != null) 
            while (node.left != null) 
                node = node.left;
            
        
        return node;
    
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

对于findMin方法，如果存在左子树，则递归遍历，终止点就是最小的元素。否则，根节点就是最小的元素。

4.insert方法
将一个新的元素X插入到树T中，可以先通过contains方法去查找该元素是否存在，如果存在，则什么都不做，否则将X插入到遍历路径上的最后一点。

public void insert(T t) 
        mRoot = insert(t, mRoot);
    

    public BinaryNode<T> insert(T t, BinaryNode<T> node) 
        if (node == null) 

            return new BinaryNode<T>(t, null, null);
        

        int compareResult = t.compareTo(node.element);
        if (compareResult > 0) 
            node.right = insert(t, node.right);
         else if (compareResult < 0) 
            node.left = insert(t, node.left);
        

        return node;
    
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

5.remove方法

public void remove(T t) 
        mRoot = remove(t, mRoot);
    

    public BinaryNode<T> remove(T t, BinaryNode<T> node) 
        if (node == null) 
            return node;
        
        int compareResult = t.compareTo(node.element);
        if (compareResult > 0) 
            node.right = remove(t, node.right);
         else if (compareResult < 0) 
            node.left = remove(t, node.left);
         else if (node.left != null && node.right != null) 
            node.element = findMin(node.right).element;
            node.right = remove(node.element, node.right);
         else 
            node = (node.left != null) ? node.left : node.right;
        
        return node;

    
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

对于删除，最复杂的是该将被删除的节点A具有两个儿子的情况，一般是该节点的右子树最小的节点B代替节点A，然后在B原来的位置删除掉节点B。

上面的代码能够完成删除工作，但效率并不高，因为它沿着树进行两趟搜索来查找和删除右子树中最小的节点。

如果删除的次数不多，通常使用懒惰删除：当一个元素要被删除时，它仍在树中，而只是标记为删除。

特别是删除算法会使得左子树比右子树深，因为我们总是用右子树的一个来代替删除的节点。会造成二叉查找树，严重的不平衡。

5.二叉查找树完整代码

public class BinarySearchTree<T extends Comparable<?
        super T>> 

    private BinaryNode<T> mRoot;

    public void makeEmpty() 
        mRoot = null;
    

    public boolean isEmpty() 
        return mRoot == null;
    

    public boolean contains(T t) 
        return contains(t, mRoot);
    

    public boolean contains(T t, BinaryNode<T> node) 
        if (t == null) 
            return false;
        

        int campareResult = t.compareTo(node.element);
        if (campareResult < 0) 
            return contains(t, node.left);
         else if (campareResult > 0) 
            return contains(t, node.right);
         else 
            return true;
        
    

    public T findMax() 
        if (isEmpty()) 
            throw new IndexOutOfBoundsException();
        
        return findMax(mRoot).element;
    

    private BinaryNode<T> findMax(BinaryNode<T> node) 
        if (node != null) 
            while (node.right != null) 
                node = node.right;
            
        
        return node;
    

    public T findMin() 
        if (isEmpty()) 
            throw new IndexOutOfBoundsException();
        
        return findMin(mRoot).element;
    

    private BinaryNode<T> findMin(BinaryNode<T> node) 
        if (node != null) 
            while (node.left != null) 
                node = node.left;
            
        
        return node;
    

    public void insert(T t) 
        mRoot = insert(t, mRoot);
    

    public BinaryNode<T> insert(T t, BinaryNode<T> node) 
        if (node == null) 

            return new BinaryNode<T>(t, null, null);
        

        int compareResult = t.compareTo(node.element);
        if (compareResult > 0) 
            node.right = insert(t, node.right);
         else if (compareResult < 0) 
            node.left = insert(t, node.left);
        

        return node;
    

    public void remove(T t) 
        mRoot = remove(t, mRoot);
    

    public BinaryNode<T> remove(T t, BinaryNode<T> node) 
        if (node == null) 
            return node;
        
        int compareResult = t.compareTo(node.element);
        if (compareResult > 0) 
            node.right = remove(t, node.right);
         else if (compareResult < 0) 
            node.left = remove(t, node.left);
         else if (node.left != null && node.right != null) 
            node.element = findMin(node.right).element;
            node.right = remove(node.element, node.right);
         else 
            node = (node.left != null) ? node.left : node.right;
        
        return node;

    

    private static class BinaryNode<T> 
        private T element;
        private BinaryNode<T> left;// 左孩子
        private BinaryNode<T> right;// 右孩子

        public BinaryNode(T element, BinaryNode<T> left, BinaryNode<T> right) 
            this.element = element;
            this.left = left;
            this.right = right;
        

        public BinaryNode(T element) 
            this(element, null, null);
        

    


 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125

二叉树的遍历

1.前序遍历
若二叉树非空，则执行以下操作：
(1) 访问根结点；
(2) 先序遍历左子树；
(3) 先序遍历右子树。

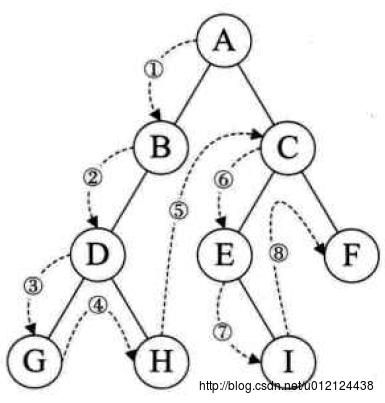
前序遍历代码

 //前序遍历
    private void preOrder(BinaryNode<T> tree) 
        if(tree != null) 
            System.out.print(tree.element+" ");
            preOrder(tree.left);
            preOrder(tree.right);
        
    

    public void preOrder() 
        preOrder(mRoot);
    
 1
2
3
4
5
6
7
8
9
10
11
12

2.中序遍历
若二叉树非空，则执行以下操作：
(1) 中序遍历左子树；
(2) 访问根结点；
(3) 中序遍历右子树。

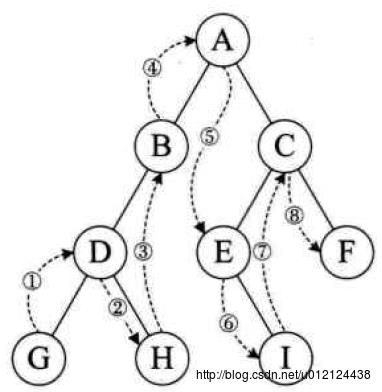
中序遍历代码

private void inOrder(BinaryNode<T> tree) 
        if(tree != null) 
            inOrder(tree.left);
            System.out.print(tree.element+" ");
            inOrder(tree.right);
        
    

    public void inOrder() 
        inOrder(mRoot);
    

 1
2
数据结构与算法问题 二叉搜索树
 数据结构与算法—查找（树表的查找）
 手撸golang 基本数据结构与算法 二叉查找树
 数据结构与算法之深入解析“验证二叉搜索树”的求解思路与算法示例
 数据结构与算法之深入解析“二叉搜索子树的最大键值和”的求解思路与算法示例
 数据结构与算法简记--红黑树