【时间序列分析】为啥要做季节调整？对数处理？差分？（理论篇）

Posted 2023-04-13

参考技术A 通常我们在对时间序列数据构建模型之前，需要对变量进行一些季节调整，对数化处理和差分处理，为甚么要这么做，不做有什么样的影响呢？

第一个问题：为什么要做季节调整？

        一般来说，一个经济指标中往往包含有四个变动要素，长期要素、循环要素、季节要素和其他一些不规则的要素。在经济分析中，往往趋势和循环要素才能真实的反映经济指标的运行的客观规律，季节变动要素比如吃冰棍的夏季往往比冬季多得多，这就会掩盖掉经济变量发展的客观规律，因此在分析之前，需要对变量做季节调整，剔除它。

          记住只有季度和月度的数据才需要调整

        采用什么方法来剔除呢？目前比较常用的有4种方法，CensusX12、X11、移动平均方法和Tramo/Seats方法。比较常用的是CensusX12方法，如何来做，操作上再说，很简单。

      那季节调整有什么样的缺点呢？说白了，季节调整后的数据，不论总量和增长速度均与实际数值存在很大的差距，数据反映出的很可能不是指标在核算期的实际经济含义。

    第二个问题：为什么要做对数化处理？

        因为大部分经济指标数据都是呈现偏态分布的，比如收入或者国民生产总值，而且这些指标大都呈现右偏，取对数可以将大于中位数的值按照比例进行缩小，从而让数据服从正态分布，而正态分布也符合计量模型中的很多假设，对于解决异方差问题有很大的帮助。

  第三个问题：为什么要差分？

        从研究的目标上来讲，对数化处理后再差分，体现的是该经济指标的对数收益率。对研究增长率相关的问题很重要。

      从统计学角度来讲，差分是非平稳序列变成平稳序列常用的方法，只有平稳性的时间序列才能避免“伪回归”的存在，才有经济意义。

数字信号处理线性常系数差分方程 ( 使用 matlab 求解 “ 线性常系数差分方程 “ 示例 | A 向量分析 | B 向量分析 | 输入序列分析 | matlab 代码 )

文章目录

• 一、使用 matlab 求解 “ 线性常系数差分方程 “ 示例
• • 1、B 向量元素 : x(n) 参数
  • 2、A 向量元素 : y(n) 参数
  • 3、输入序列
  • 4、matlab 代码

一、使用 matlab 求解 “ 线性常系数差分方程 “ 示例

---

描述 某个 " 线性时不变系统 " 的 " 线性常系数差分方程 " 如下 :

$$y(n)=1.5x(n)+0.7y(n-1)$$

输入序列 :

$$x(n)=\delta (n)$$

边界条件 / 初始条件 :

$$y(-1)=1$$

求该 LTI 系统的 输出序列 ;

线性常系数差分方程 公式 :

$$y(n)=\sum _{i=0}^M{b}_{i}x(n-i)-\sum _{i=1}^N{a}_{i}y(n-i)n\ge M$$

1、B 向量元素 : x(n) 参数

讨论 $B$ 向量 , $B$ 向量是 $x(n)$ 的参数 , 有几个 $x(n)$ 项 , $B$ 向量 就有几个元素 ;

上式中 $M=0$ , $x(n)$ 的项只有 $1$ 项 , ${\sum }_{i=0}^M{b}_{i}x(n-i)$ 只有一项 , 加和式只有一项 , 因此对应的 $B$ 向量 , 只有 $1$ 个元素 ;

B = [1.5];

2、A 向量元素 : y(n) 参数

下面讨论 $A$ 向量 , $A$ 向量是 $y(n)$ 的参数 , 有几个 $y(n)$ 项 , $A$ 向量 就有几个元素 ;

线性常系数差分方程 :

$$y(n)=1.5x(n)+0.7y(n-1)$$

将 $0.7y(n-1)$ 移到左边 , 得到 :

$$y(n)-0.7y(n-1)=1.5x(n)$$

这里有 $2$ 个 $y(n)$ 项 , $A$ 向量的元素有两个 , $1,-0.7$ ;

A = [1, -0.7];

3、输入序列

输入序列 :

$$x(n)=\delta (n)$$

输入序列 的元素个数 , 等于 输出序列 的元素个数 ;

$n=0$ 时 , $x(n)=1$ , 然后再次生成 $30$ 个 $0$ 元素 , 放到 输入序列 中 ;

输入序列为 $1,\underset{30个0}{\underbrace{0,0,\cdots ,0}}$ , 共 $31$ 个元素 ;

对应的 matlab 代码为

xn=[1,zeros(1,30)]; 

4、matlab 代码

matlab 代码 :

% 边界条件 y(-1) = 1 , 这里设置 ys = 1
ys = 1;

% 输入序列 为 单位脉冲序列
xn=[1,zeros(1,30)]; 

% 线性常系数差分方程 中的 x(n) 项系数
B=1.5;

% 线性常系数差分方程 中的 y(n) 项系数
A=[1, -0.7];

% 等效 初始条件 的 输入序列 xi
xi=filtic(B,A,ys);

% 输出序列
yn=filter(B,A,xn,xi); 

%建立幕布
figure;
%绘制 "输出序列" 图像 , 点用上三角表示
plot(yn, '^');

% 打开网格
grid on;

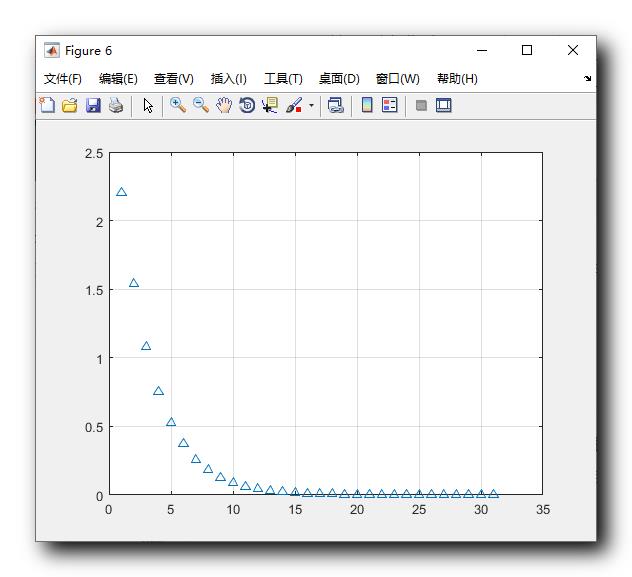
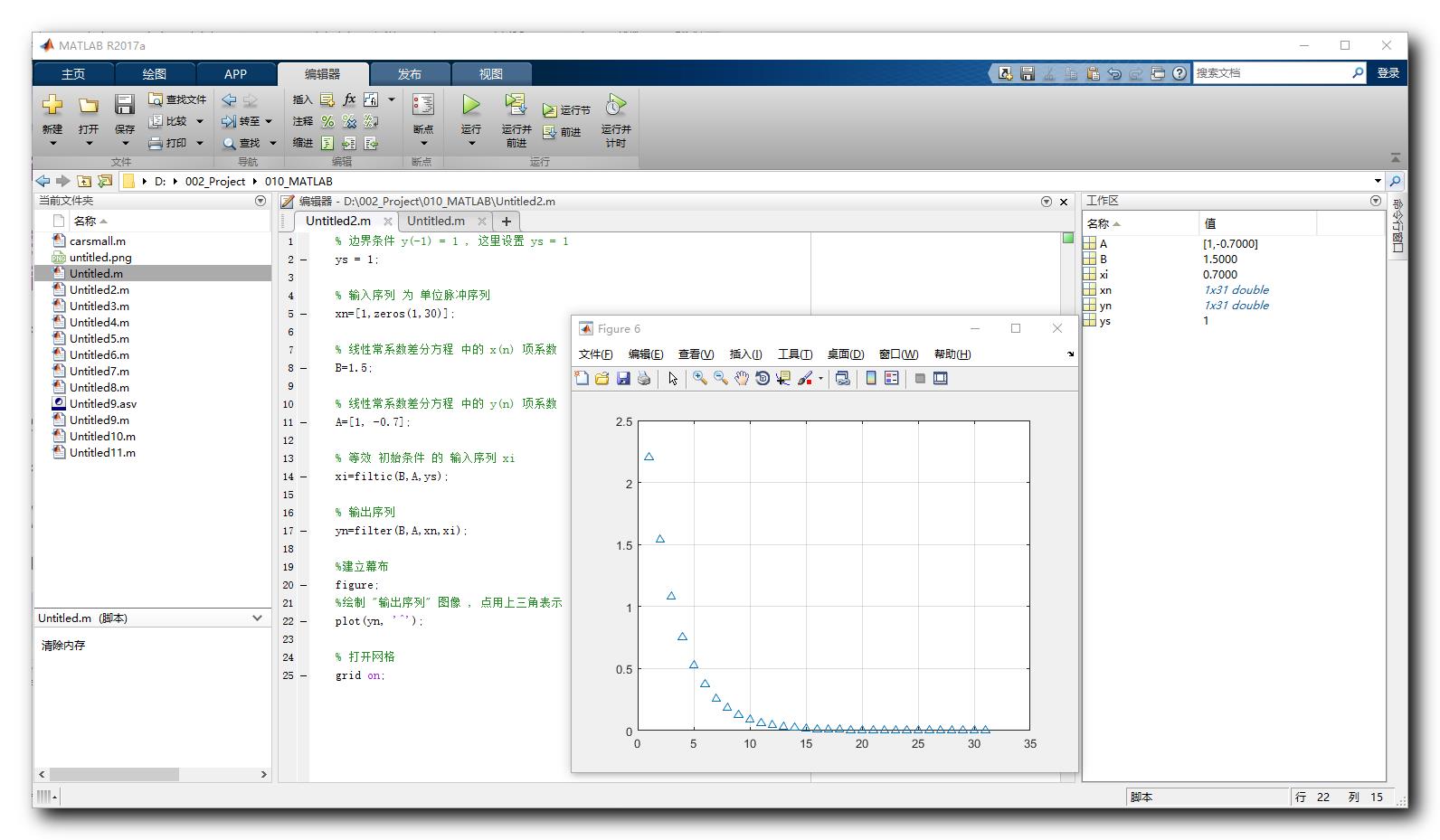
绘图效果 :