AVLTree的C++的实现

Posted 2022-12-04 别碰我的宏定义

数据结构之AVL树

文章目录

• 前言
• 一、AVL树是什么？
• • 1.1AVL树的概念
• 二、AVL树的实现
• • 1.AVL树的调整
  • • 1.1AVL树的底层树调整
    • 1.2AVL树的往上层调整
    • 1.3AVL树的调整总结
  • 2.AVL树的C++实现
• 总结

---

前言

数据结构对于每一个编程人员来说都是十分重要的，而其中的二叉树就是最鲜明的代表。让我们来一起了解其中特别有魅力的AVL树吧。

---

提示：

一、AVL树是什么？

1.1AVL树的概念

由百度百科可知其是一颗二叉平衡搜索树。其中有三点重要信息：
1、二叉树：（节点的度最多为2的树，也就是最多只能有两个孩子的树为二叉树）
2、平衡树：（就是左右子树的高度差不能超过一的树为平衡树）。
3、搜索树：（就是按照中序或者后续的方法去遍历这棵树的时候他是有序的为搜索树）
然后它大概就长下面这样。

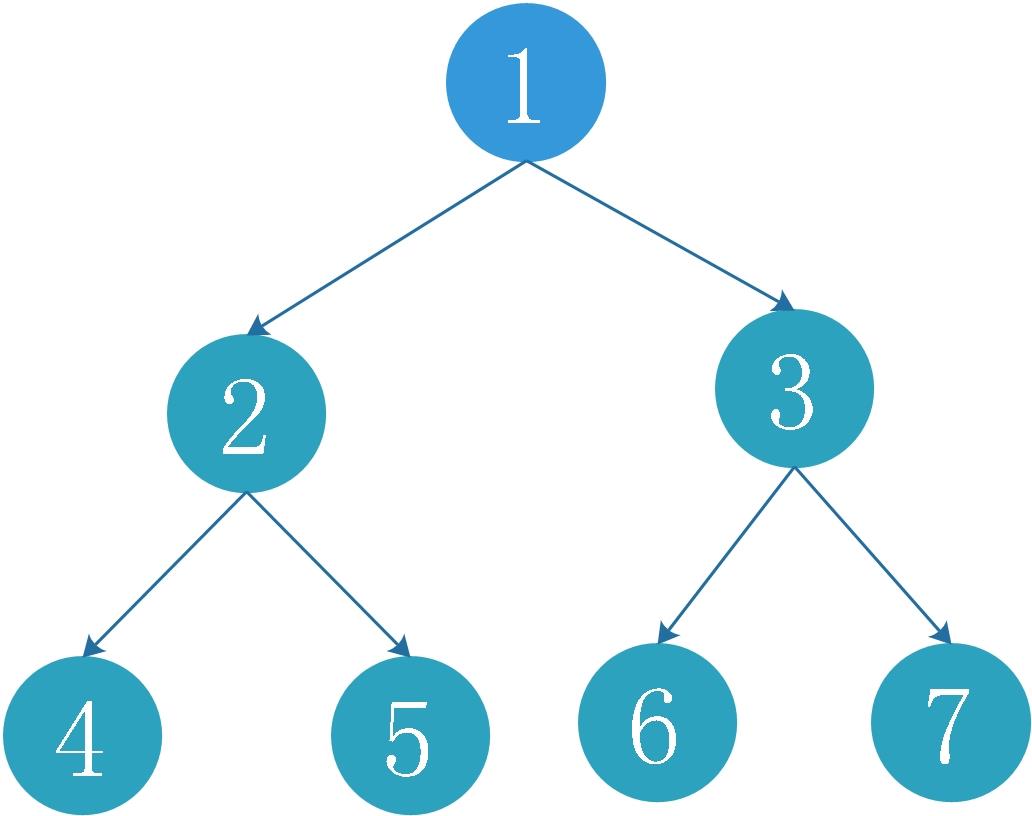
二、AVL树的实现

1.AVL树的调整

1.1AVL树的底层树调整

AVL树不满足平衡条件时肯定是因为向其某个叶子节点中添加元素导致的，所以其处理的情况有一下三种。
1.出现左右单支的情况，肯定不满足，平衡因子等于2.和-2.

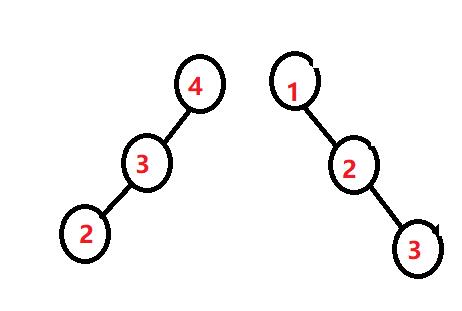
针对于左单支需要右旋，而右单支需要左旋
：
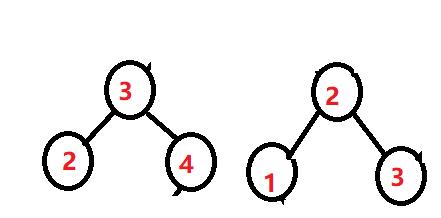
左单支：（对于本例）将节点中值为3的节点提上去作为父节点，将值为4的节点拿下来作为3的右孩子就行了。
右单支：（对于本例）将节点中值为2的节点提上去作为父节点，将值为1的节点拿下来作为左孩子就完成了。

2.当出现往左孩子的右孩子添加元素时导致的平衡因子发生改变不满足AVL树的规则

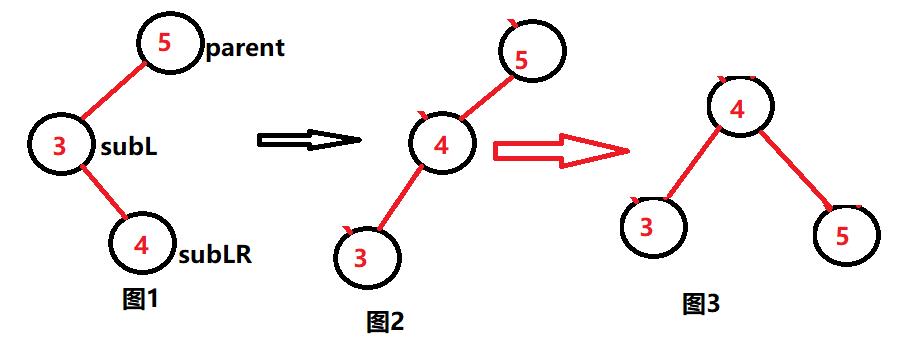
需要先以左孩子为根的树进行一次左单旋，（也就是将subL向下放，将subLR向上提），使其成为左单支的情况，然后按照左单支的情况进行一次右单旋。
3、当出现往右孩子的左孩子添加元素时导致的平衡因子发生改变不满足AVL树的规则
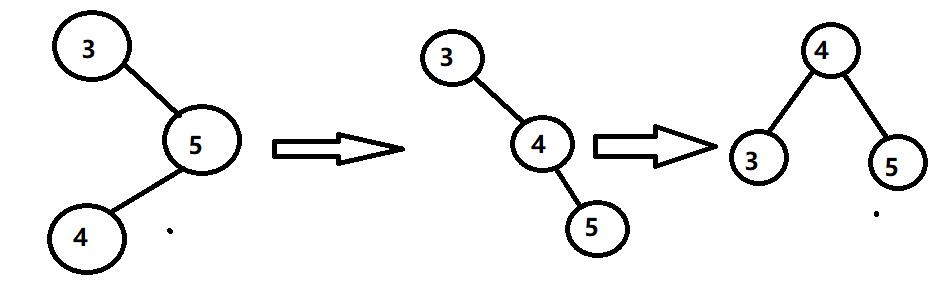需要先以右孩子为根的树进行一次右单旋，（也就是将5向下放，将4向上提），使其成为右单支的情况，然后按照右单支的情况进行一次左单旋。

1.2AVL树的往上层调整

向上层调整的时候就需要考虑到该节点的叔叔节点。两种情况。
1、该节点为父亲节点的左孩子，如果左孩子的右孩子不空，则将右孩子的父节点更改。
2、该节点为父亲节点的右孩子，如果右孩子的左孩子不空，则将右孩子的父节点更改。

1.3AVL树的调整总结

当无论处理以上哪一种情况之后就会将平衡因子处理为0，因为在添加时上层已经是AVL树了，你填加的时候只是破坏了某个节点及其以后的树的规则，故不再需要向上更新。

2.AVL树的C++实现

AVL树的节点结构，因为它需要调整树的结构及节点的位置，所以需要孩子双亲表示法去表示，并且需要在结构体中给出构造函数，在C++中的结构体的默认属性是共有的。

template<class T>
struct AVLTreeNode //定义节点类型，用孩子双亲表示法来表示
	AVLTreeNode<T>* left;
	AVLTreeNode<T>* right;
	AVLTreeNode<T>* parent;
	T data; //数据
	int bf; //平衡因子

	AVLTreeNode(const T& x) //构造函数
		:left(nullptr)
		,right(nullptr)
		,parent(nullptr)
		,data(x)
		,bf(0)
	
;

AVL树的插入实现

template<class T>
class AVLTree 
	typedef AVLTreeNode<T> Node;
public:
	//构造和析构函数
	AVLTree():root(nullptr)
	~AVLTree()  DestroyTree(root); 
	//AVLTree的插入
	bool insert(const T& val) 
		if (root == nullptr) //没有节点时，为根节点直接插入
		
			root = new Node(val);
			return true;
		

		else 
		//按照二叉搜索树的规则查找插入节点在二叉搜索树中的位置
			Node* cur = root;
			Node* parent = nullptr;//用parent来标记cur的父节点。
			while (cur) //查找该节点在AVL树中的位置。大于当前节点则在当前节点的右子树上，
			//小于当前节点，则在当前节点的左子树上。
				parent = cur;
				if (val < cur->data) 
					cur = cur->left;
				
				else if (val > cur->data) 
					cur = cur->right;
				
				else 
					return false;
				
			
			cur = new Node(val); //构造节点，
			//判断插入位置
			if (val < parent->data) 
				parent->left = cur;
			
			else 
				parent->right = cur;
			
			cur->parent = parent;
			while (parent != nullptr)
			
				//更新平衡因子
				if (cur == parent->left) 
					parent->bf--;
				
				else 
					parent->bf++;
				

				if (parent->bf == 0) 
					break;
				
				else if (parent->bf == -1 || parent->bf == 1) 
					cur = parent;
					parent = cur->parent;
				

				else 
					if (parent->bf == -2) 
						if (cur->bf == -1)  //左子树高，并且cur是其父亲的左节点
							//右单旋转
							RotateRight(parent);
						
						else //左子树高，并且cur是其父节点的右节点
							//左右双旋
							RotateLR(parent);

						
					
					else 
						if (cur->bf == 1) 
							//左单旋
							RotateLeft(parent);
						
						else 
							//右左双旋
							RotateRL(parent);
						
					
					break;
				
			
			return true;
		
	
	//验证他的正确性
	void Inorder() 
		_Inorder(root);
		cout << endl;
	
	bool isAVLTree() 
		return _isAVLTree(root);
	
private:
	bool _isAVLTree(Node* root) 
		if (root == nullptr) 
			return true;
		
		int leftHeight = TreeDepth(root->left);
		int rightHeight = TreeDepth(root->right);
		int bf = rightHeight - leftHeight; //获取平衡因子，并且依据平衡因子来查看它的正确性
		if (abs(bf) > 1 || bf != root->bf) 
			cout << root->data << ":" << bf << "------" << root->bf << endl;
			return false;
		
		//用递归的方式来查看每一个节点的正确性
		return _isAVLTree(root->left) && _isAVLTree(root->right);
	
	void RotateRight(Node* parent) 
		Node* subL = parent->left;
		Node* subLR = subL->right;
		parent->left = subLR;
		if (subLR)  //如果有右孩子，则将左孩子有右孩子，右孩子的父节点先标记为父亲节点
			subLR->parent = parent;
		
		//左单只直接将左孩子提上去当父节点
		subL->right = parent;
		
		Node* pparent = parent->parent;
		parent->parent = subL;
		subL->parent = pparent;

		//parent可能是根也可能是某一颗子树
		if (pparent == nullptr) 
			root = subL;
		
		else 
			//判断是左右孩子
			if (pparent->left == parent) 
				pparent->left = subL;
			
			else 
				pparent->right = subL;
			
		
		subL->bf = parent->bf = 0;
	
	void RotateLeft(Node* parent) 
		Node* subR = parent->right;
		Node* subRL = subR->left;
		parent->right = subRL;
		if (subRL) 
			subRL->parent = parent;
		
		//如果是右单只的情况，那么就处理父节点
		subR->left = parent;

		//还有各个节点的父节点没有处理
		Node* pparent = parent->parent;
		subR->parent = pparent;
		parent->parent = subR;
		 //判断parent是否是根节点
		if (pparent == nullptr) 
			root = subR;
		
		else 
			if (pparent->left == parent) 
				pparent->left = subR;
			
			else 
				pparent->right = subR;
			
		
		subR->bf = parent->bf = 0;
	
	void RotateLR(Node* parent) 
		Node* subL = parent->left;
		Node* subLR = subL->right;
		int bf = subLR->bf;
		RotateLeft(parent->left);
		RotateRight(parent);
		if (bf == -1)
			parent->bf = 1;
		else if (bf == 1)
			subL->bf = -1;
	
	void RotateRL(Node* parent) 
		Node* subR = parent->right;
		Node* subRL = subR->left;
		int bf = subRL->bf;
		RotateRight(parent->right);
		RotateLeft(parent);

		if (-1 == bf) 
			subR->bf = 1;
		
		else if (1 == bf) 
			parent->bf = -1;
		
	

	void DestroyTree(Node*& proot) 
		if (proot) 
			DestroyTree(proot->left);
			DestroyTree(proot->right);
			delete proot;
			proot = nullptr;
		
	
	int TreeDepth(Node* root) 
		if (root == nullptr)
			return 0;
		int leftDepth = TreeDepth(root->left);
		int rightDepth = TreeDepth(root->right);
		return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
	
	void _Inorder(Node* proot) 
		if (proot) 
			_Inorder(proot->left);
			cout << proot->data << " ";
			_Inorder(proot->right);
		
	
private:
	Node* root; //定义根节点
;
void TestAVLTree() 
	int a[] =  4,2,6,1,3,5,15,7,16,14 ;
	AVLTree<int> t;
	for (auto e : a) 
		t.insert(e);
	
	t.Inorder();
	if (t.isAVLTree()) 
		cout << "this is AVLTree" << endl;
	
	else 
		cout << "this isn't AVLTree" << endl;
	

---

总结

对于AVL树：以上就是今天要讲的内容，本文仅仅简单介绍了AVL树元素的添加以及树的旋转过程。核心要点是对于其四种旋转的理解。