深度学习入门基础二简单理解 Transformer
Posted 陆嵩
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了深度学习入门基础二简单理解 Transformer相关的知识，希望对你有一定的参考价值。
【深度学习入门基础】二、简单理解 Transformer
文章目录
这是“深度学习入门基础”系列的第二篇文章，事多更新慢，望见谅。前一篇文章（先导篇）见：
【深度学习入门基础】一、从线性代数和微积分的角度看神经网络
ResNet 和 Transformer 近五年来是影响最深远的两个网络结构，没有之一，bert 也是从 Transformer 发展而来。近年来，Transformer 更是从 NLP 领域走入了 CV 领域，似乎什么东西都可以 attention 一下，大有一统天下之势。
因为 Transformer 很火，所以网上的各式各样的讲解很多，我就不介绍（chao xi）了，意义不大。本文依然秉承先导篇的代数风格，我们对 Transformer 做一个简单的总结。为了方便入门，我将尽可能少地去引入一些新名词。
自注意力层
Transformer 的核心是 self-attention layer，所以，我们先介绍一下这是个什么东西。
它是一个变换，把一个输入序列，变成一个输出序列。如图所示，
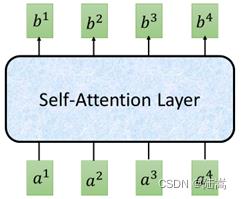
它把 4 个向量 a 1 , a 2 , a 3 , a 4 a_1,a_2,a_3,a_4 a1,a2,a3,a4 输入（习惯上，下面所有的向量一般都是指列向量），通过的一波瞎操作，变成了 4 个向量输出 b 1 , b 2 , b 3 , b 4 b_1,b_2,b_3,b_4 b1,b2,b3,b4。那么，这一波瞎操作是什么呢？看过先导篇的直到，神经网络层无非是一些“矩阵乘向量”的函数表示，那么这一波瞎操作，无非就是一些代数运算，人们称之为 Self-Attention Layer。
下面我们开门见山地给出这一波瞎操作。假设输入是一组列向量
x
i
，
i
=
1
,
⋯
,
n
x_i，i=1,\\cdots,n
xi，i=1,⋯,n，输入也是一组列向量，
y
i
，
i
=
1
,
⋯
,
n
y_i，i=1,\\cdots,n
yi，i=1,⋯,n，我们把输入输出按行排成一个矩阵，即
X
=
[
x
1
,
x
2
,
⋯
,
x
n
]
X = [x_1,x_2,\\cdots,x_n]
X=[x1,x2,⋯,xn]
Y
=
[
x
1
,
x
2
,
⋯
,
x
n
]
Y = [x_1,x_2,\\cdots,x_n]
Y=[x1,x2,⋯,xn]
那么，attention 做的事情无非就是，
A
=
W
X
A=WX
A=WX
Y
=
W
V
A
softmax
(
(
W
K
A
)
T
W
Q
A
d
)
Y = W_VA\\operatornamesoftmax\\left(\\frac(W_KA)^TW_QA\\sqrt d\\right)
Y=WVAsoftmax(d(WKA)TWQA)
其中，
softmax
\\operatornamesoftmax
softmax 作用在矩阵上分别对每一列做
softmax
\\operatornamesoftmax
softmax，
softmax
(
M
)
i
j
=
e
M
i
j
∑
i
=
1
N
e
M
i
j
\\operatornamesoftmax(M)_ij=\\frace^M_ij\\sum_i=1^Ne^M_ij
softmax(M)ij=∑i=1NeMijeMij
其中，
W
,
W
V
,
,
W
K
,
W
Q
W,W_V,,W_K,W_Q
W,WV,,WK,WQ 都是一些参数矩阵，
d
=
W
K
的
行
数
=
W
Q
的
行
数
d = W_K 的行数 = W_Q 的行数
d=WK的行数=WQ的行数。参数矩阵的大小要令等式 make sense 即可。令
W
V
A
=
V
,
W
K
A
=
k
,
W
Q
A
=
Q
W_VA = V,W_KA = k,W_QA=Q
WVA=V,WKA=k,WQA=Q，那么上面的公式可以简记为：
Y
=
V
softmax
(
K
T
Q
d
)
Y = V \\operatornamesoftmax\\left(\\fracK^TQ\\sqrt d\\right)
Y=Vsoftmax(dKTQ)
看公式总是可以接受，但是不太好形象地理解，有点莫名其妙。没关系，可以看看李宏毅老师的对 transformer 的宇宙最强解释，他的 PPT 做的我认为极好。
多头注意力
什么是 multi-head self-attention？假设我们有多组 K , Q , V K,Q,V K,Q,V，那么就可以得到多组的 Y Y Y，这些组的 Y Y Y 可以揉成一个 Y Y Y。多组 K , Q , V K,Q,V K,Q,V 的可以原始的一组“分裂”得到。多组的 Y Y Y 揉成一个 Y Y Y 可以通过在行方向上串联，再乘以一个系数矩阵得到。
细致地说，假设
Q
,
K
,
V
Q,K,V
Q,K,V 通过如下方式分裂成
h
h
h 个头，
K
i
=
W
K
,
i
K
,
i
=
1
,
⋯
,
h
K_i = W_K,iK, \\space i=1,\\cdots,h
Ki=WK,iK, i=1,⋯,h
Q
i
=
W
Q
,
i
Q
,
i
=
1
,
⋯
,
h
Q_i = W_Q,iQ, \\space i=1,\\cdots,h
Qi=WQ,iQ, i=1,⋯,h
V
i
=
W
V
,
i
V
,
i
=
1
,
⋯
,
h
V_i = W_V,iV, \\space i=1,\\cdots,h
Vi=W《自然语言处理实战入门》深度学习基础 ---- attention 注意力机制 ，Transformer 深度解析与学习材料汇总
《自然语言处理实战入门》深度学习基础 ---- attention 注意力机制 ，Transformer 深度解析与学习材料汇总
深度学习/机器学习入门基础数学知识整理：Jensen不等式简单理解，共轭函数