深度剖析HMM（附Python代码）3.隐马尔科夫链所解决的问题

Posted 2022-12-03 tostq

通过隐马尔科夫链，有以下几方面功能：

1. 解码问题

 已知某一序列，找到最可能的隐藏状态序列（即所谓的解码问题，利用维比特算法来解决）

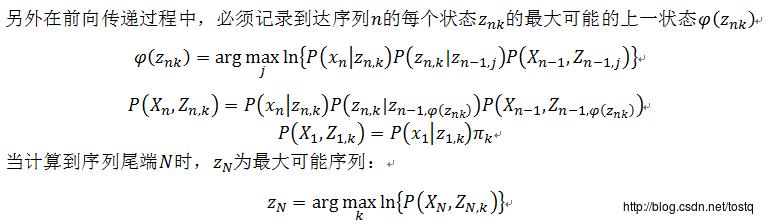
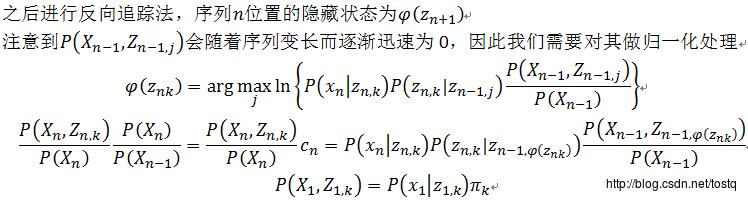
解码过程的相关python代码

    def decode(self, X, istrain=True):
        """
        利用维特比算法，已知序列求其隐藏状态值
        :param X: 观测值序列
        :param istrain: 是否根据该序列进行训练
        :return: 隐藏状态序列
        """
        if self.trained == False or istrain == False:  # 需要根据该序列重新训练
            self.train(X)

        X_length = len(X)  # 序列长度
        state = np.zeros(X_length)  # 隐藏状态

        pre_state = np.zeros((X_length, self.n_state))  # 保存转换到当前隐藏状态的最可能的前一状态
        max_pro_state = np.zeros((X_length, self.n_state))  # 保存传递到序列某位置当前状态的最大概率

        _,c=self.forward(X,np.ones((X_length, self.n_state)))
        max_pro_state[0] = self.emit_prob(X[0]) * self.start_prob * (1/c[0]) # 初始概率

        # 前向过程
        for i in range(X_length):
            if i == 0: continue
            for k in range(self.n_state):
                prob_state = self.emit_prob(X[i])[k] * self.transmat_prob[:,k] * max_pro_state[i-1]
                max_pro_state[i][k] = np.max(prob_state)* (1/c[i])
                pre_state[i][k] = np.argmax(prob_state)

        # 后向过程
        state[X_length - 1] = np.argmax(max_pro_state[X_length - 1,:])
        for i in reversed(range(X_length)):
            if i == X_length - 1: continue
            state[i] = pre_state[i + 1][int(state[i + 1])]

        return  state

2. 观测问题

确定一段序列出现的概率

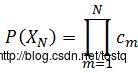
相关Python代码：

    # 估计序列X出现的概率
    def X_prob(self, X, Z_seq=np.array([])):
        # 状态序列预处理
        # 判断是否已知隐藏状态
        X_length = len(X)
        if Z_seq.any():
            Z = np.zeros((X_length, self.n_state))
            for i in range(X_length):
                Z[i][int(Z_seq[i])] = 1
        else:
            Z = np.ones((X_length, self.n_state))
        # 向前向后传递因子
        _, c = self.forward(X, Z)  # P(x,z)
        # 序列的出现概率估计
        prob_X = np.sum(np.log(c))  # P(X)
        return prob_X

3. 预测观测值（预测问题）

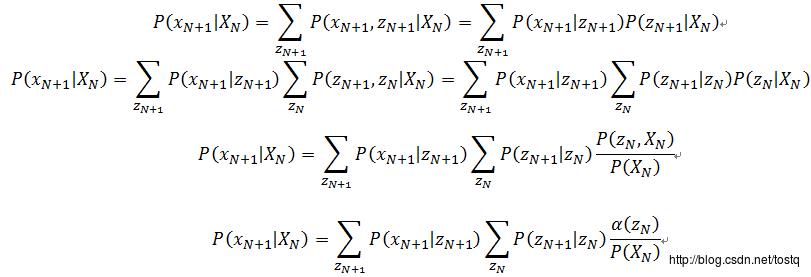
由上可知，要预测观测值必须知道过去的隐藏状态值，从而确定转换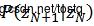概率和发射概率，然后可以确定下一观测值的概率，如果不确定过去的隐藏状态值，可以先通过维特比算法确定最有可能的隐藏状态序列。

相关Python代码：

    # 已知当前序列预测未来（下一个）观测值的概率
    def predict(self, X, x_next, Z_seq=np.array([]), istrain=True):
        if self.trained == False or istrain == False:  # 需要根据该序列重新训练
            self.train(X)

        X_length = len(X)
        if Z_seq.any():
            Z = np.zeros((X_length, self.n_state))
            for i in range(X_length):
                Z[i][int(Z_seq[i])] = 1
        else:
            Z = np.ones((X_length, self.n_state))
        # 向前向后传递因子
        alpha, _ = self.forward(X, Z)  # P(x,z)
        prob_x_next = self.emit_prob(np.array([x_next]))*np.dot(alpha[X_length - 1],self.transmat_prob)
        return prob_x_next

4. 生成问题（生成一段序列）

相关Python代码：

    # 通过HMM生成序列
    def generate_seq(self, seq_length):
        X = np.zeros((seq_length, self.x_size))
        Z = np.zeros(seq_length)
        Z_pre = np.random.choice(self.n_state, 1, p=self.start_prob)  # 采样初始状态
        X[0] = self.generate_x(Z_pre) # 采样得到序列第一个值
        Z[0] = Z_pre

        for i in range(seq_length):
            if i == 0: continue
            # P(Zn+1)=P(Zn+1|Zn)P(Zn)
            Z_next = np.random.choice(self.n_state, 1, p=self.transmat_prob[Z_pre,:][0])
            Z_pre = Z_next
            # P(Xn+1|Zn+1)
            X[i] = self.generate_x(Z_pre)
            Z[i] = Z_pre

        return X,Z

PS：

项目说明：http://blog.csdn.net/tostq/article/details/70846702

代码下载：https://github.com/tostq/Easy_HMM （点星是对作者最好的支持！！！^_^）