第三节4：类K-Means算法之二分K-均值算法（bisecting K-Means算法）

Posted 2022-12-03 我擦我擦

文章目录

• 一：算法思想
• 二：算法流程
• 三：Python实现
• 四：效果展示
• 五：优缺点

一：算法思想

二分K-均值算法（bisecting K-Means）：这是一种结合了层次聚类思想的K-均值变种算法。其基本思想是：将所有点看成一个簇，为了得到最终要求的$k$个簇，就将这个簇分裂为两个簇，之后迭代这个过程，每次都选取一个现有的簇进行分裂，所选取簇要能够最大化程度降低SSE

二：算法流程

输入：数据集D，聚类个数k
输出：k个簇

1：初始化簇表，使之包含由所有数据点所组成的一个簇
2：repeat
3:		for 簇表中的一个簇
4：			使用标准k-均值方法对选定的簇进行聚类，其中k值设定为2
5：			计算SSE是否小于lowestSSE，则更新lowestSSSE，并保存至最优划分
6：		选择最优划分，将这个两个簇添加到簇表中
7：until 簇表中包含k个簇

三：Python实现

from array import array

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from numpy import mean
from sklearn.cluster import KMeans

# 欧氏距离计算
def euclidean_distance(vec1, vec2):
    return np.sqrt(np.sum(np.power(vec1-vec2, 2)))
# 初始化随机质心
def centorids_init(data_set, k):
    examples_nums = np.shape(data_set)[0]  # 样本数量
    random_ids = np.random.permutation(examples_nums)  # 随机打乱序列
    centorids = data_set[random_ids[:k], :]  # 随机选取k质心
    return centorids
# KMeans算法
def kmeans(data_set, k):
    example_nums = np.shape(data_set)[0]
    # 第一列是数据点归属，第二列是每个样本点距其所属簇质心的距离
    labels = np.mat(np.zeros(shape=[example_nums, 2]))
    # 质心
    centroids = centorids_init(data_set, k)
    flag = True
    while flag:
        flag = False
        # 对于每个样本点计算它到所有质心的距离
        for i in range(example_nums):
            min_dist = np.inf
            cluster_index = -1
            for j in range(k):
                dist_ji = euclidean_distance(centroids[j, :], data_set[i, :])
                if dist_ji < min_dist:
                    min_dist = dist_ji
                    cluster_index = j
            # 如果发生了变化，继续
            if labels[i, 0] != cluster_index:
                flag = True
            # 确定给数据归属
            labels[i, :] = cluster_index, min_dist**2
        # 重新计算质心
        for cent in range(k):
            ptsInclust = data_set[np.nonzero(labels[:, 0] == cent)[0]]
            centroids[cent, :] = np.mean(ptsInclust, axis=0)
    return centroids, labels

def bisecting_kmeans(data_set, k):
    example_nums = np.shape(data_set)[0]
    labels = np.mat(np.zeros(shape=[example_nums, 2]))
    # 把所有数据看成一个簇，计算出均值
    centroid0 = np.mean(data_set, axis=0).tolist()[0]
    # 簇表
    centlist = [centroid0]
    # 计算每个点到质心的距离
    for j in range(example_nums):
        labels[j, 1] = euclidean_distance(np.mat(centroid0), data_set[j, :]) ** 2

    # 开始循环，直到达到目标簇个数
    while len(centlist) < k:
        # 初始化SSE
        lowestSSE = np.inf
        for i in range(len(centlist)):
            # 把每一个簇看作成一个小的数据集
            ptsInCurrCluster = data_set[np.nonzero(labels[:, 0] == i)[0], :]
            # 对这个数据集进行KMeans，k设置为2
            centroidMat, splitLabels = kmeans(ptsInCurrCluster, 2)
            sseSplit = np.sum(splitLabels[:, 1])  # 划分数据的SSE
            sseNotSplit = np.sum(labels[np.nonzero(labels[:, 0] != i), 1])  # 未划分数据的SSE
            # 总和SSE如果小于最小SSE，确定可以划分
            if(sseSplit + sseNotSplit) < lowestSSE:
                bestCentToSplit = i  # 当前最适合做划分的中心点
                bestNewCents = centroidMat  # 划分后的两个中心点
                bestLabels = np.copy(splitLabels)  # 划分后的聚类信息
                lowestSSE = sseSplit + sseNotSplit  # 更新lowsetSSE

        bestLabels[np.nonzero(bestLabels[:, 0] == 1)[0], 0] = len(centlist)
        bestLabels[np.nonzero(bestLabels[:, 0] == 0)[0], 0] = bestCentToSplit

        # 更新簇表
        centlist[bestCentToSplit] = bestNewCents[0, :].tolist()[0]
        centlist.append(bestNewCents[1, :].tolist()[0])
        labels[np.nonzero(labels[:, 0] == bestCentToSplit)[0], :] = bestLabels
    return np.mat(centlist), labels

raw_data = pd.read_csv(r'E:\\Postgraduate\\Dataset\\melon.csv', header=None)
#raw_data.columns = ['X', 'Y', 'Z']
raw_data.columns = ['X', 'Y']

x_axis = 'X'
y_axis = 'Y'
#z_axis = 'Z'

examples_num = raw_data.shape[0]
train_data = raw_data[['X', 'Y']].values.reshape(examples_num, 2)
train_data = train_data.copy(order='C')



min_vals = train_data.min(0)
max_vals = train_data.max(0)
ranges = max_vals - min_vals
normal_data = np.zeros(np.shape(train_data))
nums = train_data.shape[0]
normal_data = train_data - np.tile(min_vals, (nums, 1))
normal_data = normal_data / np.tile(ranges, (nums, 1))


centroids, labels = bisecting_kmeans(np.mat(normal_data), 4)

# 原数据
fig, (ax0, ax1) = plt.subplots(ncols=2)
ax0.scatter(normal_data[:, 0], normal_data[:, 1], c='black')
ax0.set_title('raw data')
# 谱聚类结果

ax1.scatter(normal_data[:, 0], normal_data[:, 1], c=np.array(labels)[:, 0])
ax1.set_title('Birch Clustering')

ax1.scatter(centroids[:, 0].tolist(), centroids[:, 1].tolist(), c='red', marker='x')


plt.show()

四：效果展示

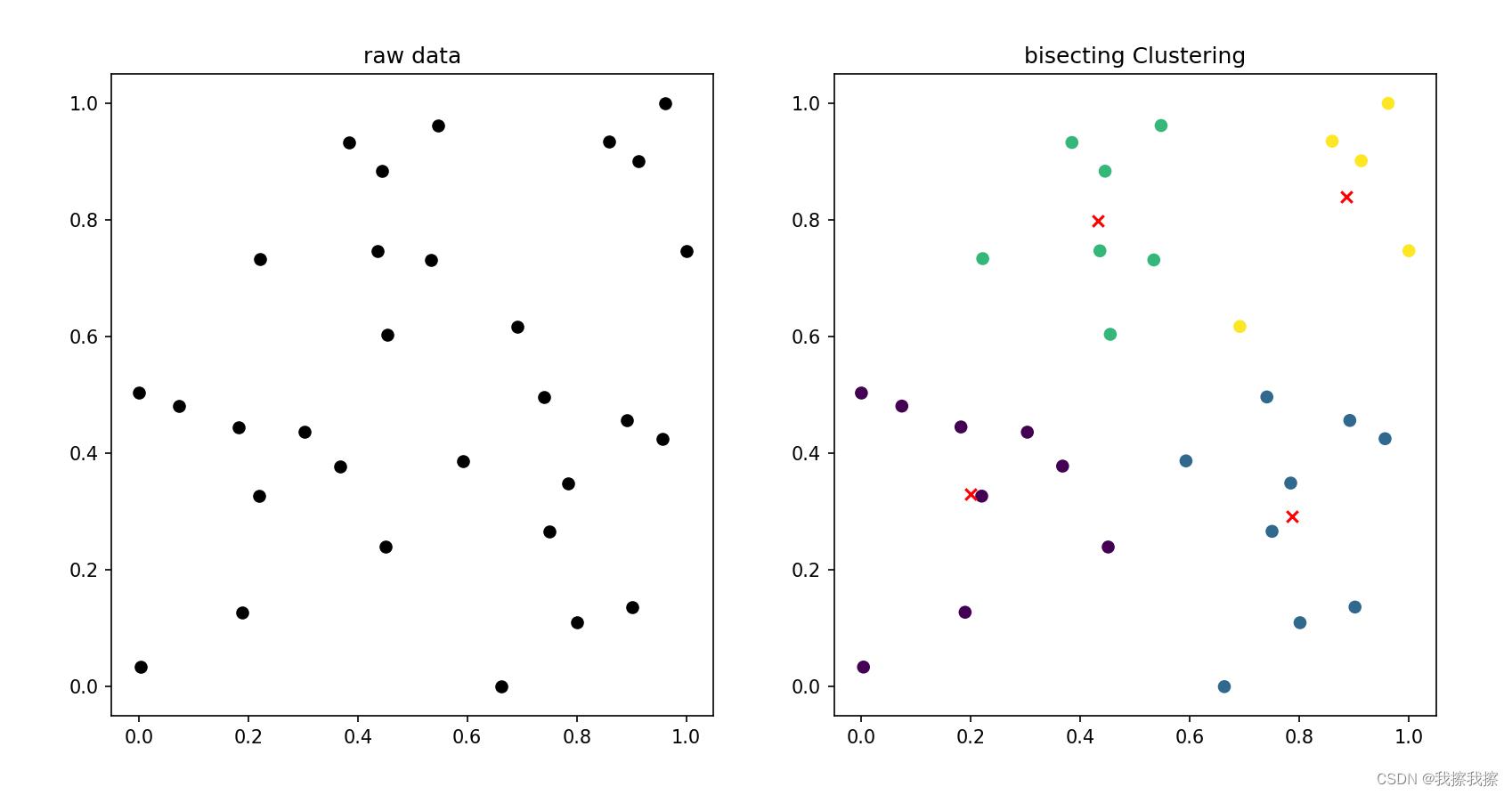
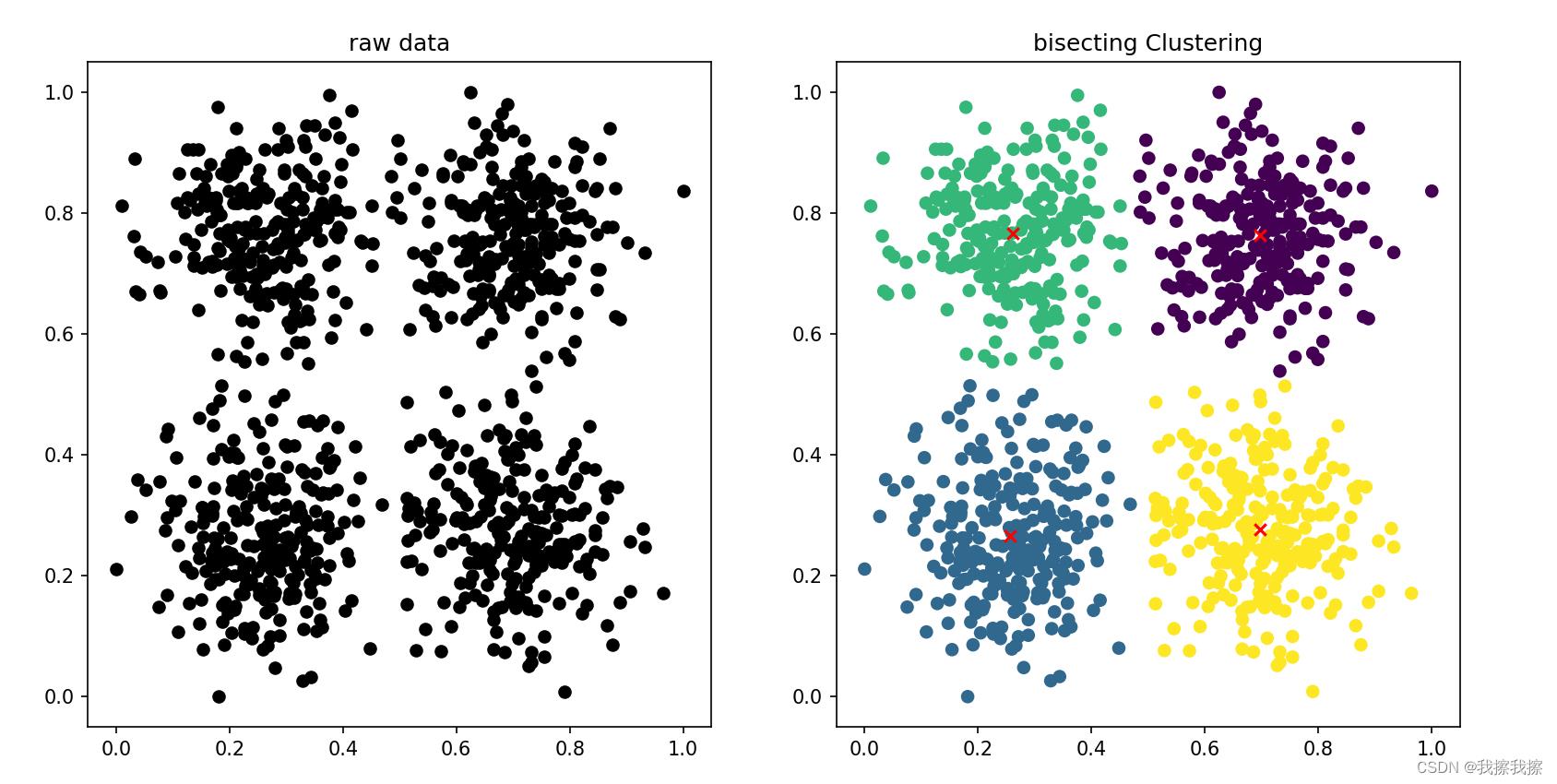
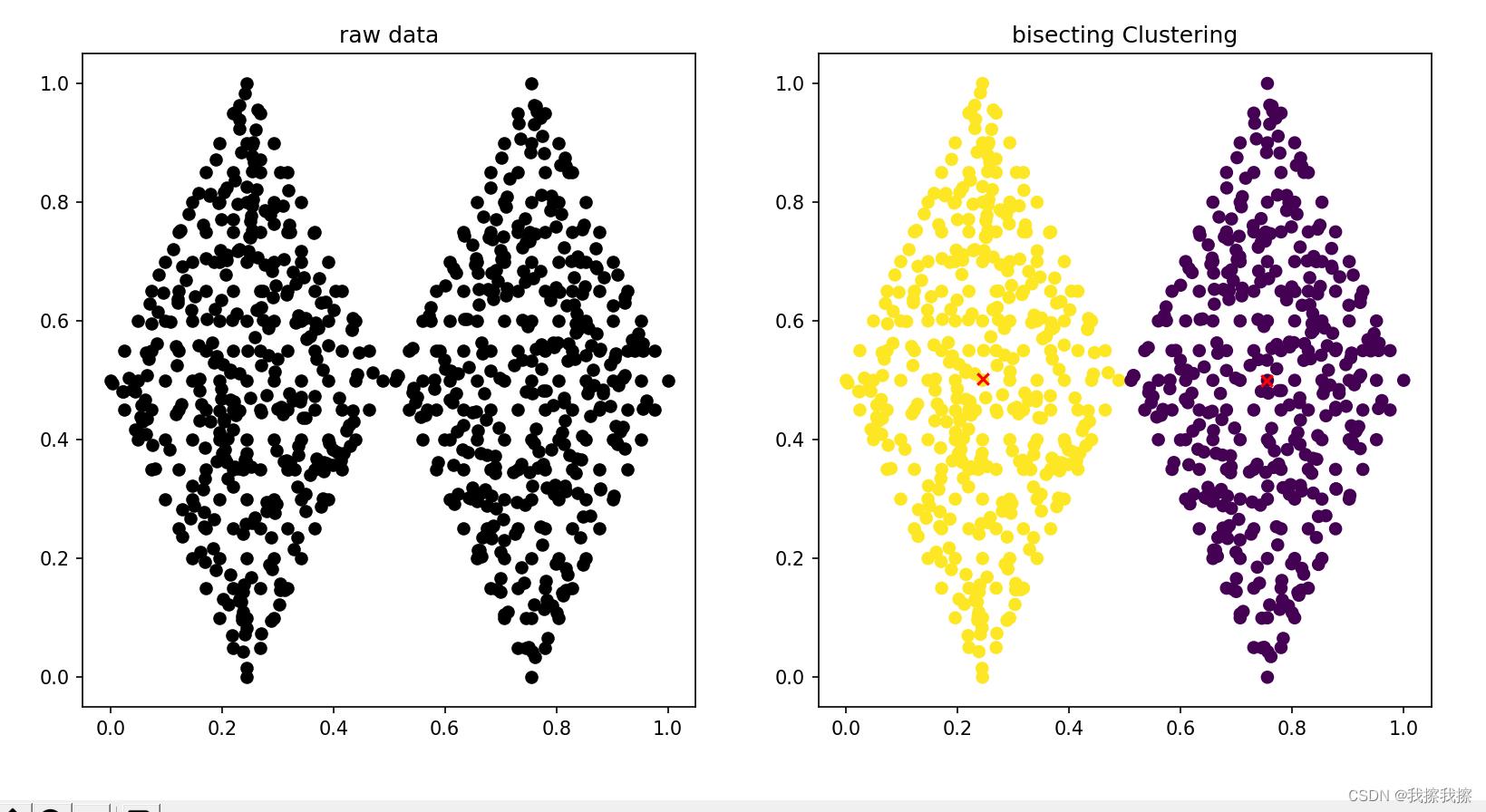
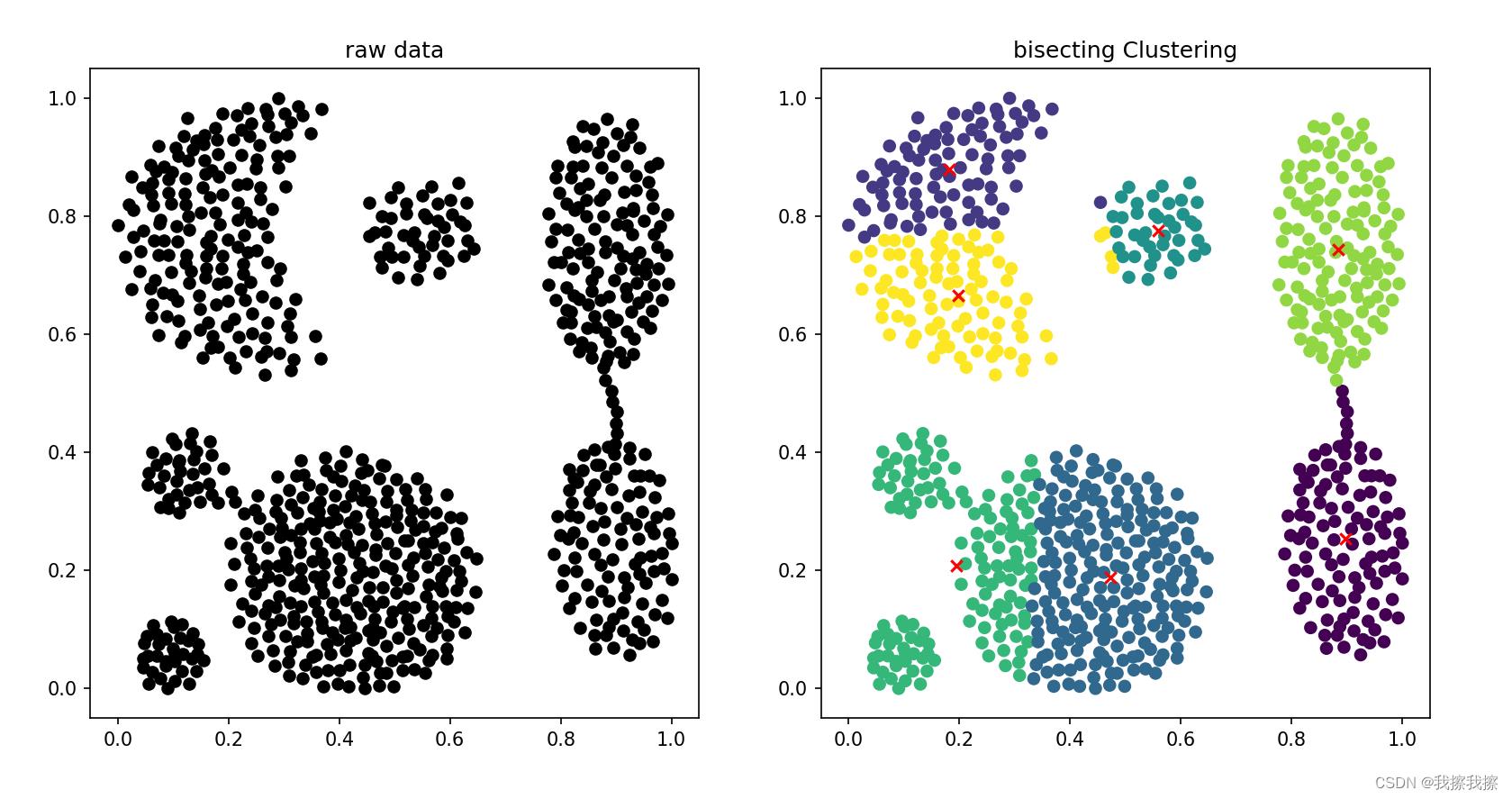
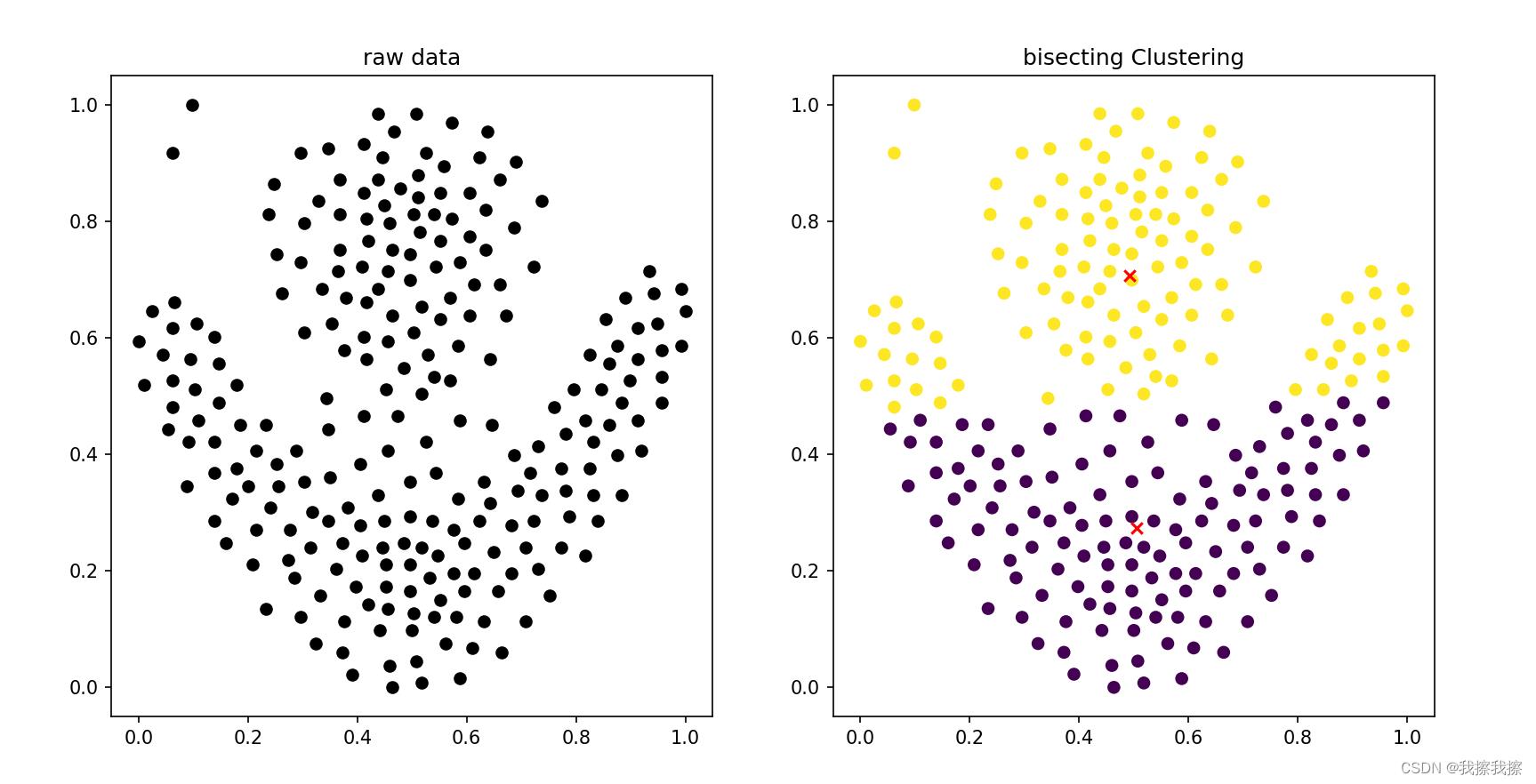
五：优缺点

由于是二分K-均值算法的改进算法，所以优缺点和其基本一致，主要区别有

• 二分k-均值算法在时间上的花销是远高于标准k-均值算法的，但是由此带来的聚类结果的保证弥补了这一损失，相当于用时间上的开销来换取性能上的稳定性
• 二分k-均值算法可以很好地抵抗初始化问题的干扰，所以可以将其作为一种标准k-均值算法的预处理方法