牛客多校训练赛补题
Posted Hellsegamosken
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了牛客多校训练赛补题相关的知识,希望对你有一定的参考价值。
集训终于结束了,这个成绩挺出乎我的预料。不论牛客还是杭电,正常发挥20多名,发挥好了能打到十几名。包括昨天 CCPC 预选赛打了第十名(zcq yyds),给我一种选对赛站能出线的感觉?虽然打出来的成绩是以前没想到的,但是这 20 场比赛一场一场打下来以后,我也深刻体会到有很多地方还有不足,而且训练赛三人三机也和正式比赛不一样。
继续加油
目录
- contest2
- contest3
- contest4
- contest5
- contest6
- contest7
- contest9
- contest10
- 2019 ICPC Asia Xuzhou Regional
contest2
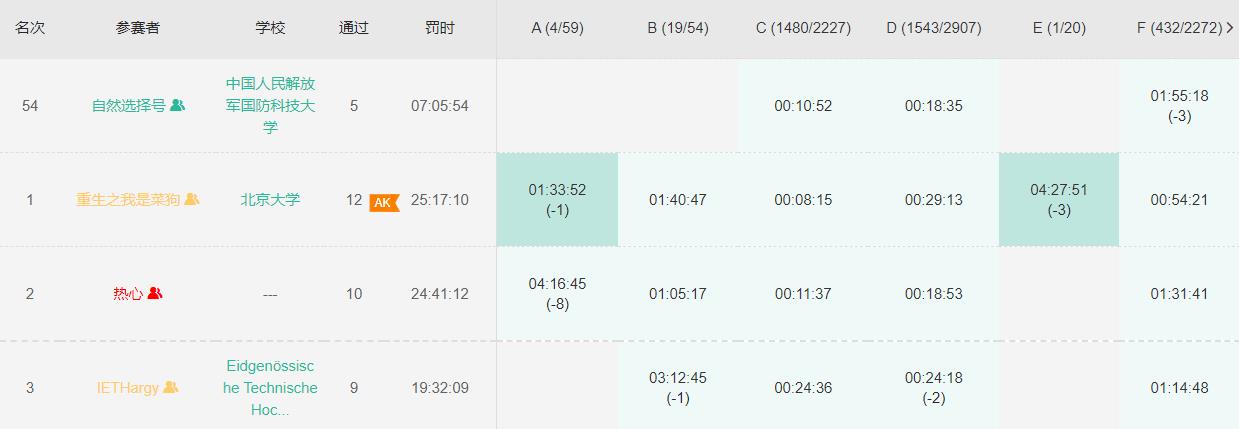
A - Arithmetic Progression

第一步观察就没看出来…
首先,b 的公差一定是 g c d i = 1 n − 1 b i + 1 − b i gcd_i=1^n-1\\b_i + 1 - b_i\\ gcdi=1n−1bi+1−bi。因此相当于判断 ( r − l + 1 ) ⋅ g c d i = 1 n − 1 b i + 1 − b i − m a x b i + m i n b i (r - l +1) · gcd_i=1^n-1\\b_i + 1 - b_i\\ - max\\b_i\\ + min\\b_i\\ (r−l+1)⋅gcdi=1n−1bi+1−bi−maxbi+minbi 是不是等于 0。
枚举右端点,用线段树维护左端点。max 和 min 用单调栈处理即可。注意到
- 对于一个右端点,gcd 不同的左端点至多 log 段。
- 对于一个左端点,右端点右移的过程中 gcd 最多变化 log 次。
因此右端点移动的时候,对于 gcd 不变的左端点,由于 1,可以进行 log 段区间加;对于 gcd 变化的左端点,由于 2,暴力单点修改即可。
注意到,需要单点修改的左端点一定是一个后缀。用一个栈维护一下 log 段 gcd 的右端点即可。
contest3
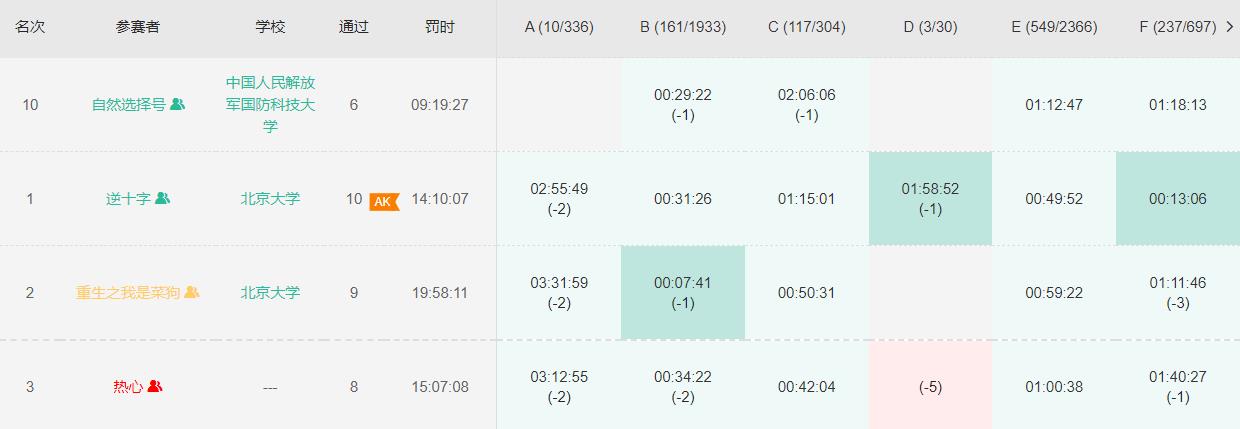
G - Yu Ling(Ling YueZheng) and Colorful Tree

颜色范围 [1, n]。
容易想到构建 n 棵树,第 i 棵树上存放颜色是 i 的倍数的点的信息。因为保证颜色两两不重复,因此总点数是 nlogn 的。之后,对于某个询问,相当于在某一刻线段树上查询颜色在某个范围内的,某个点的最近祖先。注意到还有一个时间维度。
我考场上的做法是在最外围处理时间,抛开时间限制之后,离线,在线段树上 dfs,用 n 棵线段树维护当前点到根这条链上的信息即可(第 i
个叶子维护颜色 i 到根的距离,查询区间最大值),这部分是两个 log。至于外面时间的处理,可以 cdq + 虚树加一个 log,但我实在懒得写,因此用分块重构的方法,调整块大小为 n^0.8 左右复杂度和三个 log 差不多,但并没有通过此题。
考后看了逆十字的代码。注意到边权为正,因此“最近祖先”这个东西是可以二分的。因此问题转化成每次给某个点一个数,询问某个点向上的某条祖先链有没有范围在某个区间内的数。这是个二维信息,“祖先链”这一维可以在 dfs 序上用树状数组解决,另一维就是线段树了。于是这题就三个 log 解决了。
I - Kuriyama Mirai and Exclusive Or

感觉这是个神仙题啊… orz zcq
第一种操作好说,关键是第二种操作。
发现对于第 i 位,异或的序列一定是有 2^(i+1) 的周期。如果把原序列的每 2^(i+1) 个元素作为一行,那么会惊喜的发现所有 1 会形成 O(1) 个矩形!然后二维差分即可。
contest4

B - Sample Game

提供一个生成函数的做法。
令
f
(
x
)
=
∑
i
=
0
∞
P
(
l
e
n
>
i
)
x
i
f(x) = \\sum_i=0^\\inftyP(len>i)x^i
f(x)=∑i=0∞P(len>i)xi
根据题意,有
f
(
x
)
=
∏
i
(
1
+
p
i
x
+
p
i
2
x
2
+
.
.
.
)
=
∏
i
1
1
−
p
i
x
f(x) = \\prod_i(1 + p_ix + p_i^2x^2 +...) = \\prod_i\\frac11-p_ix
f(x)=∏i(1+pix+pi2x2+...)=∏i1−pix1
答案是
∑
i
=
0
∞
(
P
(
l
e
n
>
i
)
−
P
(
l
e
n
>
i
+
1
)
)
i
2
=
∑
i
=
1
∞
P
(
l
e
n
>
i
)
(
i
2
−
(
i
−
1
)
2
)
=
∑
i
=
1
∞
P
(
l
e
n
>
i
)
(
2
i
−
1
)
=
\\beginaligned & \\sum_i=0^\\infty(P(len>i)-P(len>i+1))i^2\\\\ = & \\sum_i=1^\\inftyP(len>i)(i^2-(i-1)^2)\\\\ = & \\sum_i=1^\\inftyP(len>i)(2i-1)\\\\ = & \\endaligned
===i=0∑∞(P(len>i)−P(len>i+1))i2i=1∑∞P(len>i)(i2−(i−1)2)i=1∑∞P(len>i)(2i−1)
D - Rebuild Tree
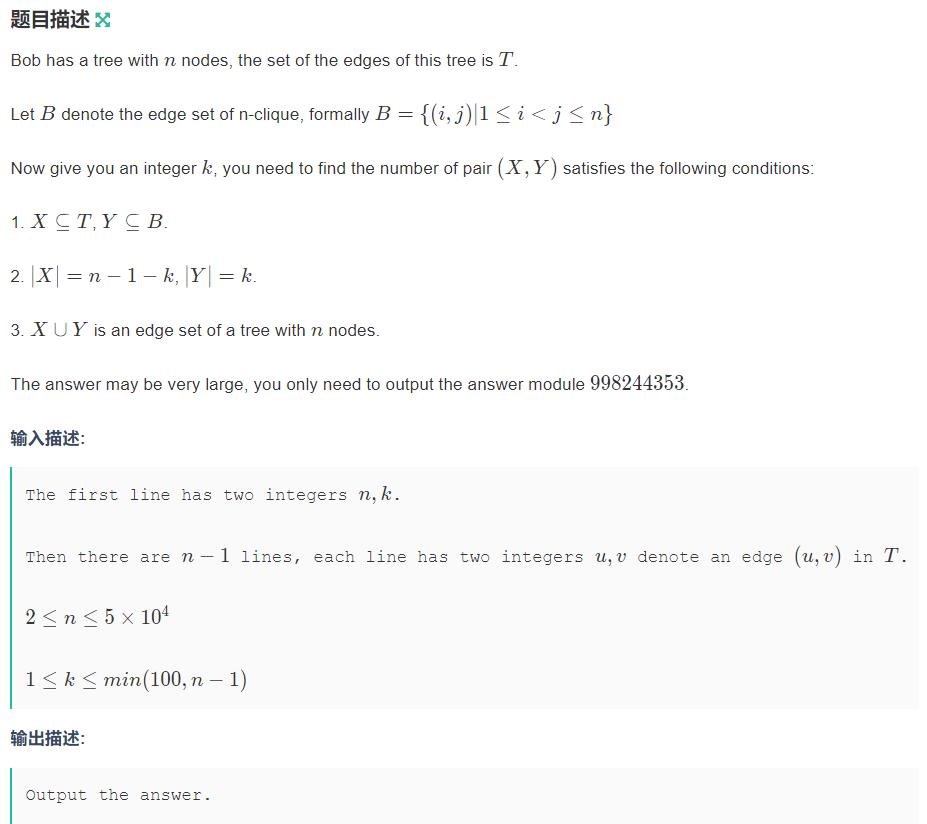
题意是给定一棵树,删除 k 条边,再任意加 k 条边使得它还是一棵树,求方案数。
回忆 prufer 序列,就是每次删除最小点把它的相邻点加入序列中。序列长度 n − 2 n-2 n−2,每个点在序列中出现 d i − 1 d_i - 1 di−1 次。因此 n 个点的树有 n n − 2 n^n-2 nn−2 种。
容易发现,假设删完边以后剩下的联通快大小是 a 1 , . . . , a k a_1,...,a_k a1,...,ak,那么在这种删边方式下的方案数有 k k − 2 ∏ a i d i = ∑ p i a i n u m i ∏ i a i k^k-2\\prod a_i^d_i=\\sum_p_ia_i^num_i\\prod_i a_i kk−2∏aidi=∑piainumi∏iai,其中最外面的 sigma 是枚举 k k − 2 k^k-2 kk−2 种 prufer 序列, n u m i num_i numi 是第 i 个联通快在 prufer 序列中出现的次数。我到了这里就推不下去了。
其实这个式子还没有推到底。注意到 ∑ p i a i n u m i \\sum_p_ia_i^num_i ∑piainumi 相当于有 k-2 个位置,每个位置可以选 a 1 , . . . , a k a_1,...,a_k a1,...,ak 中的任何一个,再相乘的方案数。因此它也就等于 ( ∑ a i ) k − 2 = n k − 2 (\\sum a_i)^k-2=n^k-2 (∑a